Purpose

We propose a data-driven reconstruction method which conditions a reverse diffusion process ¹ with physics-informed data consistency steps. The approach was tested in fast spiral dynamic cardiac MRI at 1.5T.

Methods

Score-based generative model
A score-based generative model ^1,2 was used to learn the distribution of a database consisting of 23156 cardiac MR images (data source: ³). To this end, a neural network was trained to reverse the process of noise being iteratively added to instances/images of the database. This model can be interpreted as a reverse-time stochastic differential equation (rSDE) which is – after successful training - capable of iteratively transforming Gaussian noise into a sample of the given distribution, i.e. an artificial cardiac MR image.
The dataset we used for training ³ consists of magnitude reconstructions without any complex phase or coil information, as typically stored in picture archiving and communication systems. Fig. 1 illustrates both the training and the sampling process and shows exemplary artificial images generated by the model.

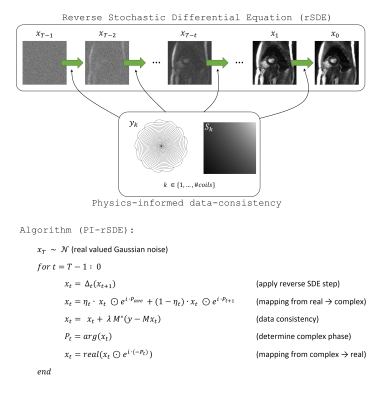
Conditioning the rSDE with physics-informed data consistency (PI-rSDE)
To exploit the modelling capacity of the trained rSDE for the reconstruction of accelerated dynamic cardiac MR measurements (“cine”), the $$$T$$$ reverse time generative steps were each conditioned by undersampled multi-coil k-space data (“physics-informed”-rSDE: PI-rSDE, see Fig. 2 and compare ^2,4). Each 2D image of the series was reconstructed separately in our approach. Let $$$M = \Omega F S$$$ be the MR measurement operator, which maps an image $$$x$$$ to undersampled complex-valued multi-coil k-space data $$$y$$$, according to: $$$y = M x$$$. $$$S$$$ holds the information on the coil sensitivities which was determined from a temporal average image across all cardiac frames, $$$F$$$ is the Fourier transform, and $$$\Omega$$$ applies a sampling mask with undersampling factor $$$R$$$. For $$$t = T-1, …, 0$$$ let $$$\Delta_t$$$ further denote the $$$t$$$-th reverse SDE step, mapping a real-valued $$$x_{t+1}$$$ to a real-valued $$$x_t$$$ with reduced noise.
The complex phase of each cine image to be reconstructed was again initially approximated by the phase $$$P_{ave}$$$of a fully sampled temporal average image, i.e. mean image across all frames. This phase was linearly transferred towards the phase of the image estimated in the previous iteration $$$P_{t+1}$$$. The reconstruction of one frame $$$x$$$ was performed by the proximal gradient descent type algorithm outlined in Fig. 2 ($$$T = 500, \eta_t = 1 - \frac{1}{T}, \lambda = 1$$$). In contrast to e.g. ², the regularizer $$$\Delta_t$$$ thus has to be applied just once (on the magnitude image of a coil combined version of $$$x_t$$$) in each iteration.

Test Data
The proposed method was tested in cardiac cine imaging at 1.5 T (Siemens MAGNETOM Avanto) for different undersampling rates $$$R$$$. A GSTF-corrected ⁵ spiral bSSFP pulse sequence (TR = 3.8 ms) with golden angle increment between consecutive readouts was used. Data were acquired for approx. 15s in a mid-ventricular slice of a healthy volunteer during breath-hold. Different subsets were then built from these data, corresponding to virtual acquisitions lasting for $$$h$$$ heartbeats ($$$h$$$= 1,2,…13).
For each subset, data were segmented into 30 bins (i.e. cardiac phases), using the k-space centre for self-gating. The average temporal resolution was 40 ms, while spatial resolution was 1.6 mm × 1.6 mm × 8 mm. Non-Cartesian data of each frame was transferred to a Cartesian grid using GROG ⁶ before applying the above described algorithm (PI-rSDE).
For comparison, the same data was subjected to iterative SENSE ⁷ (30 iterations), a low rank plus sparse approach (LRS ⁸), and a Unet ⁹. The latter was trained in a supervised manner on the same 23156 cardiac MR (magnitude) images used for the rSDE model, which were each paired with a retrospectively undersampled version.

Results

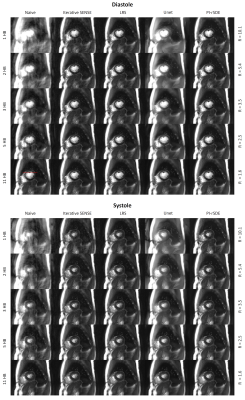
Figure 3 shows reconstructions of a diastolic and a systolic frame for several acceleration factors and the different reconstruction techniques. Iterative SENSE delivers robust reconstructions at lower acceleration rates with increasing noise for higher $$$R$$$. The additional model-based regularization of the LRS method led to higher SNR and less artifacts, especially for acquiring only 1-3 heartbeats. The data-driven reconstruction by the trained Unet did not generalize well to our test data. Severe blurring can be seen already for moderate undersampling. Note that this is the only model which did not use any information on the coil sensitivities. The proposed PI-rSDE model shows the lowest overall artifact level and highest SNR across all acceleration factors. This is confirmed by a study on the standard deviation determined in a static ROI in the spleen (see Figure 4). Visually, no blurring over iterative SENSE reconstructions is apparent for PI-rSDE which is confirmed by the 1D spatial profiles through the heart, presented in Fig. 5. Application of PI-rSDE for all 30 frames took about 54 minutes on an Nvidia RTX A6000 GPU.

Discussion

The results obtained with the proposed approach show promising potential for the successful usage of reverse diffusion models for the reconstruction of undersampled MR data. The presented approximation of the complex phase of the estimated image allowed for training the model on magnitude data only, as well as for fast inference, since the proximal operator had to be applied just once for each step.