Synopsis

Keywords: Arterial spin labelling, Perfusion, Brain

Arterial spin labeling (ASL) is a non-invasive MRI technique that allows to quantitatively measure cerebral blood flow. However, the major limitation of ASL is in the intrinsically low signal-to-noise ratio (SNR). Balanced steady-state free precession (bSSFP) sequence has been proposed to mitigate this limitation, however, bSSFP is sensitive to off-resonance effects. ASL perfusion imaging with bSSFP can be sensitive to effects from motion and flow when Cartesian sampling scheme is used. This work proposes and investigates radial sampling scheme for ASL with bSSFP to allow perfusion imaging with relatively high SNR and robustness to motion and off-resonance effects.

Introduction

Arterial spin labeling (ASL) is a non-invasive MRI technique that allows to quantitatively measure cerebral blood flow. Despite the advantages and usefulness, the major disadvantage of ASL is in the intrinsically low signal-to-noise ratio (SNR) that it can provide. Balanced steady-state free precession (bSSFP), a sequence that is known to provide the highest SNR per unit time¹, has been proposed for ASL perfusion imaging^2,3 with great potential to mitigate this limitation. However, bSSFP is sensitive to off-resonance effects which results in banding artifacts in regions with severe B₀ inhomogeneity¹. Also, ASL perfusion imaging with bSSFP can be sensitive to effects from motion and flow when Cartesian sampling scheme is used³. In this work, we propose radial sampling scheme for ASL perfusion imaging with bSSFP. The usefulness of radial sampling scheme is demonstrated for ASL perfusion imaging with bSSFP via in vivo studies from healthy volunteers.

Methods

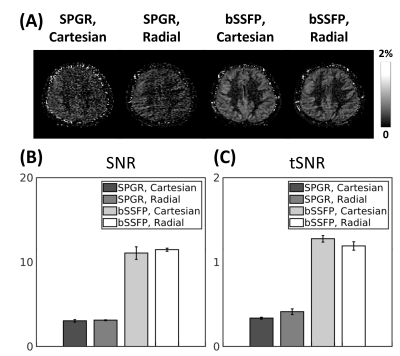
In vivo experiments were performed using a 3T MR scanner (MAGNETOM Prisma, Siemens Healthineers, Erlangen, Germany) with body-coil for signal transmission and 32-channel head coil for signal reception. The study protocol was approved by our local Institutional Review Board. ASL perfusion imaging was performed using pseudo-continuous ASL (pCASL) labeling scheme^4,5 and background suppression (BS)⁶ with the following parameters: labeling duration=1.5s; post-labeling delay (PLD)=1.5s; labeling plane= 8.5cm inferior to the anterior commissure-posterior commissure (AC-PC) line; Hanning window-shaped RF pulse; B1 average=1.63$$$\mu$$$T; average labeling gradient=1.0mT/m; slice-selective labeling gradient=6.0mT/m; and unbalanced tagging scheme. The general imaging parameters for bSSFP were: TR/TE=4∕2 ms; flip angle=30$$$^{\circ}$$$; receiver bandwidth=592Hz/pixel; and RF phase increment ($$$\triangle\phi$$$)$$$=\pi/2$$$, unless otherwise noted. For all studies, a single scan without pCASL labeling and BS was additionally acquired for quantification of the perfusion signal.

A 2D perfusion imaging study was performed to compare the differences between bSSFP and spoiled gradient echo (SPGR) sequences with Cartesian and radial sampling schemes. The common imaging parameters were: field-of-view (FOV)=240$$$\times$$$240 and 180$$$\times$$$180mm² for Cartesian and radial sampling schemes, respectively; resolution=1.875$$$\times$$$1.875mm²; slice thickness=5mm; acquisition time per imaging session=3.8min; and number of imaging sessions=3. The imaging parameters specific to SPGR were: TR/TE=4/1.7ms; flip angle=10$$$^{\circ}$$$; and receiver bandwidth=1400Hz/pixel.

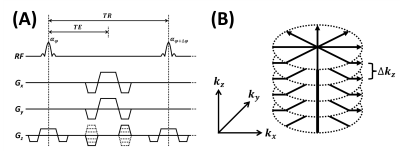
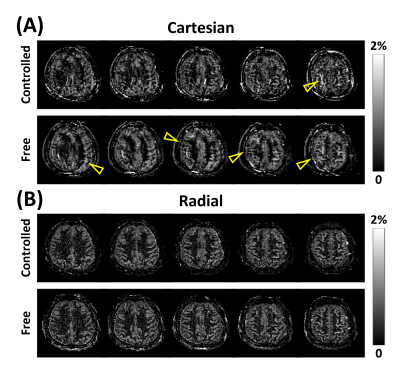
To investigate the performance with respect to respiratory-related motion, a 3D perfusion imaging study was performed using segmented 3D acquisitions of bSSFP following Cartesian and stack-of-stars sampling trajectory (Fig.1), with and without controlled breathing strategy⁷. In the case of controlled breathing, subjects were instructed to breathe voluntarily while holding their breath at times of image acquisitions. The remaining imaging parameters of bSSFP were: FOV=240$$$\times$$$240$$$\times$$$120 and 180$$$\times$$$180$$$\times$$$120mm³ for Cartesian and radial sampling schemes, respectively; resolution = 1.875$$$\times$$$1.875$$$\times$$$5mm³; and acquisition time= 4.6min.

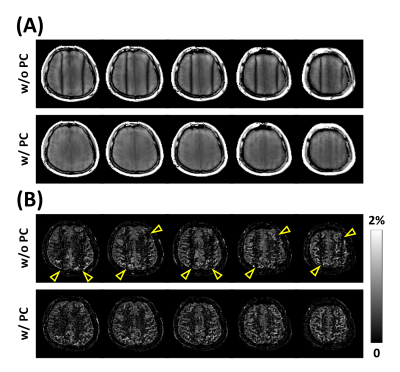
To investigate the feasibility and effect of combining with phase-cycling technique, a 3D perfusion imaging study was performed using segmented 3D acquisitions of bSSFP following stack-of-stars sampling trajectory (Fig.1), with and without phase-cycling. Additional linear gradient of 100 $$$\mu$$$T/m was applied along the right-left direction after shimming to induce banding artifacts along the direction. The remaining imaging parameters of bSSFP were: FOV=180$$$\times$$$180$$$\times$$$60mm³; resolution=1.875$$$\times$$$1.875$$$\times$$$5mm³; and acquisition time=4.6min. In case of phase-cycling, phase-cycled images were acquired with $$$\triangle\phi=0$$$,$$$\pi/2$$$,$$$\pi$$$,$$$3\pi/2$$$ and were combined using a nonlinear averaging method⁸.

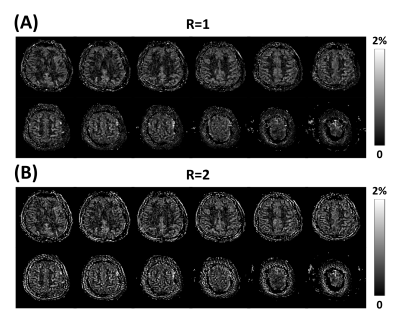
To investigate the feasibility of accelerating the imaging time, additional 3D perfusion imaging study was performed using segmented 3D acquisition of bSSFP following stack-of-stars sampling trajectory (Fig.1). The remaining imaging parameters of bSSFP were: FOV=180$$$\times$$$180$$$\times$$$120mm³; resolution = 1.875$$$\times$$$1.875$$$\times$$$5mm³; and acquisition time=2.3min and 1.15 min for full and under-sampled cases, respectively. In case of under-sampling, data was prospectively under-sampled with reduction factor (R) of 2. Image reconstruction was performed by solving the following optimization problem:
$$ \arg\min_{x}\parallel\Omega\mathcal{F}Sx-y\parallel^2_2+\lambda TV(x)$$
where $$$x$$$ denotes the reconstructed image, $$$\Omega$$$ denotes the sampling mask, $$$\mathcal{F}$$$ denotes the spatial Fourier transform, $$$S$$$ denotes the coil sensitivity, $$$y$$$ denotes the measured k-space data, $$$\lambda$$$ denotes the regularization parameter, and $$$TV(\cdot)$$$ denotes total variation regularization⁹. Non-uniform fast Fourier transform (NuFFT)¹⁰ was used for $$$\mathcal{F}$$$. The optimization problem was solved using SENSE-based reconstruction algorithm^11,12 with alternating direction method of multipliers (ADMM)¹³.

Results and Discussion

ASL with bSSFP showed higher spatial and temporal SNRs of the perfusion signal compared to those with SPGR (Fig.2). Cartesian and radial sampling schemes showed similar performance in terms of spatial and temporal SNRs of the perfusion signal, regardless of the imaging sequence (Fig.2). ASL perfusion imaging with bSSFP and Cartesian sampling scheme was sensitive to effects from respiratory-related motion, resulting in artifacts in the perfusion-weighted images (Fig.3a). In comparison, ASL perfusion imaging with bSSFP and radial sampling scheme was robust to these effects (Fig.3b). Banding artifacts were observed in the images from the single RF phase incremented bSSFP acquisitions when additional linear gradient was applied after shimming (Fig.4). Effects from these artifacts were significantly reduced when phase-cycling technique was used (Fig.4). Perfusion-weighted images were successfully reconstructed from under-sampled acquisition, demonstrating the feasibility of accelerating the imaging time for pCASL-bSSFP with radial sampling (Fig.5).

Conclusion

ASL with bSSFP and radial sampling scheme allows perfusion imaging with relatively high SNR and robustness to motion. Additional robustness to off-resonance effects can be achieved by employing phase-cycling technique. Imaging time of the proposed method can be accelerated with the help of under-sampling and image reconstruction.

Acknowledgements

This work was supported in part by the National Institutes of Health (P41EB022544, R01CA165221, R01HL137230, T32EB013180, and K01EB030045).