Synopsis

Keywords: Motion Correction, Image Reconstruction

Compressed sensing-based motion state-resolved image reconstruction (such as XD-GRASP) is computationally demanding, requiring iterative NUFFT operations. In addition, each individual echo is independently treated/reconstructed so that R2* relaxation rate with clinically significant information about tissue iron concentration may not be considered properly, causing unreliable R2* measurement. We propose a low-rank tensor-based 5D (3D space + 1D motion state + 1D echo) image reconstruction method that resolves motion states, accounts for consistency in echo evolution, and does not require iterative NUFFT operations. For in vivo human liver imaging, the proposed method showed superior image quality and R2* accuracy over existing methods.

Introduction

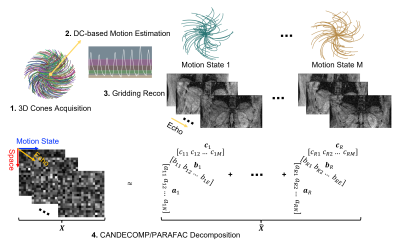
Non-Cartesian MRI has been recently investigated to address the challenge with respiratory motion in conventional gradient-echo Cartesian MRI for liver iron quantification^1,2. To further correct for respiratory motion, motion state-resolved image reconstruction such as XD-GRASP³ is required. However, compressed sensing-based XD-GRASP reconstruction is inherently iterative and requires performing forward and backward NUFFT operations per iteration, exacerbating reconstruction time of 3D non-Cartesian MRI data as opposed to stack-of-radial/spiral. Furthermore, each individual echo is treated/reconstructed independently with the existing motion-resolved or retrospective self-gating (hard gating) so that inconsistency along the echo dimension can cause unreliable R2* measurement. In this work, we propose a low-rank tensor-based multidimensional image reconstruction method that does not require iterative NUFFT operations and considers full 5D spatiotemporal imaging data in reconstruction.

Theory

We consider CANDECOMP/PARAFAC Decomposition (CPD)^4,5 with total variation regularization⁶ along the echo and motion state dimension as follows:$$\hat{X}=\underset{X}{argmin}\frac{1}{2}\left \| X-\hat{X} \right \|_{2}^{2}+\lambda_{1}\left \| \bigtriangledown_{m}\hat{X} \right \|_{1}+\lambda_{1}\left \| \bigtriangledown_{e}\hat{X} \right \|_{1},$$ $$subject\, to\, \hat{X}\approx [[A, B, C]]\equiv \sum_{r=1}^{R}a_{r}\circ b_{r}\circ c_{r},$$where $$$X$$$ is a third-order tensor with space (i.e. flattened 3D volume), echo, and motion state; $$$\lambda_{1}$$$ and $$$\lambda_{2}$$$ are regularization parameters; $$$\bigtriangledown_{m}$$$ and $$$\bigtriangledown_{e}$$$ are gradient operators with respect to the motion state and echo; $$$R$$$ is rank; and $$$a_r, b_r, c_r$$$ are the rank-one components of the factor matrices $$$A$$$, $$$B$$$, and $$$C$$$. To solve the above constrained optimization problem, alternating gradient descent algorithm⁷ was performed as shown in Fig. 2. Hereafter, we call the method CPDTV.

Methods

With IRB approval, one healthy volunteer and one patient with suspected or known iron overload were imaged with a 3T clinical MRI scanner (SignaPremierXT, GE Healthcare, Waukesha, WI). 3D multi-echo Cartesian was performed with a single breath-hold, and 3D multi-echo UTE cones MRI was performed with free breathing. Imaging parameter should go here CPDTV for image reconstruction and magnitude-based R2* mapping were performed. ROIs were placed on the liver tissue avoiding large vessels in coronal and axial views. For comparison, gridding-based non-iterative reconstruction (motion-averaged recon and hard-gating with 17% of data use), model-based iterative motion state-resolved reconstruction (XD-GRASP), and CPD were implemented and applied to the acquired data.
3D Cartesian images were acquired using a commercially available chemical-shift-encoded multi-echo spoiled gradient echo sequence (IDEAL-IQ, GE Healthcare, Waukesha, WI) with the following parameters: Matrix size = 128 162(168) 36(32), in-plane resolution = 2.9(1.78)2.3(1.78) mm2, slice thickness = 6(8) mm, FA = 3, initial TE/TE/TR = 0.684(1.064)/0.6(0.86)/5.3(7) ms, rBW = 1562(1116) Hz/Px, ETL/#shots = 3/2, acceleration = 4 , scan time = ~30 sec with a single breath-hold.3D multi-echo UTE cones acquisitions were performed following parameters: Matrix size = 190(226) 190(226) 100(120), in-plane resolution = 2 2 mm2, slice thickness = 2 mm, FA = 3, initial TE/TE/TR = 0.032/1.4/11.4(11.5) ms, #TEs = 6, readout duration = ~1ms, no acceleration, scan time = ~7 min with free breathing of subjects.

Results

Reconstructed images of the healthy volunteer are shown in Fig. 3. Motion states were clearly resolved in (B)-(E) compared to (A). In addition, undersampling artifacts were substantially removed in CPDTV (E) compared to (B)-(D) across the echoes and motion states. Similar to the image quality of individual echoes and motion states, R2* of CPDTV exhibits the minimal amount of undersampling artifacts as shown in Fig. 4. The absolute of the mean difference in ROI-based R2* between BH Cartesian and CPDTV was 8.28s-1 in coronal and 1.02s-1 in axial, and the discrepancy in R2* between the two motion states was 6.21s-1, which were smaller than other methods. Likewise, R2* maps of the patient with iron overload are shown in Fig. 5. CPDTV shows the minimal difference in R2* to BH Cartesian in coronal view and comparable difference in axial view with CPD. Yet, CPDTV shows better image quality than CPD and other methods in terms of undersampling artifacts. Reconstruction time of CPDTV was ~1h on an NVIDIA A6000 GPU which achieved 12X speedup compared to ~12h reconstruction time of motion state-resolved reconstruction.

Discussion

We have proposed a novel tensor-based multidimensional reconstruction method (CPDTV) for 5D (3D space + 1D motion state + 1D echo evolution) imaging data. CPDTV does not require iterative forward/backward NUFFT operations, so that shorter reconstruction time was achieved. The major difference from CPD is that CPDTV utilizes correlation along the motion and echo dimension via total variation regularization which was shown to be effective in undersampling artifact reduction. However, due to nonlinear optimization for each of the factor matrices, gradient descent was employed so that the total number of iterations for CPDTV to converge was greater than CPD that computes pseudoinverse. Future work will focus on strategies for data parallelism and distributed computing for further speedup.

Conclusion

Tensor-based CPDTV shows the minimal undersampling artifacts and accurate R2* measurements with shorter reconstruction time, accounting for consistency in echo evolution which was not considered in the existing methods.

Acknowledgements

This work was supported by Institute of Information & communications Technology Planning & Evaluation (IITP) grant funded by the Korea government(MSIT) (No.2021-0-02068, Artificial Intelligence Innovation Hub) In addition, this work was supported by a National Research Foundation of Korea (NRF) grant funded by the Korean government(MSIT) (project BK21 FOUR).