Introduction

Myocardial strains and microstructure are considered important indicators of muscle contractility and function^1-5. Cardiac diffusion tensor imaging (cDTI) allows investigating the microstructure of the myocardium² which is linked to contraction patterns and myofiber rearrangement. Cardiac muscle contractility has also been inferred upon by measuring tissue velocity during contraction and relaxation^3-5. In the present work we hypothesize that, by including Hadamard velocity encoding into cDTI protocols^6,9, it is possible to jointly estimate tissue velocities and local diffusion tensors without increasing scan durations. To this end we performed simulations incorporating cardiac contractile motion and model based diffusion to study the accuracy of joint tissue velocity and diffusion tensor mapping.

Methods

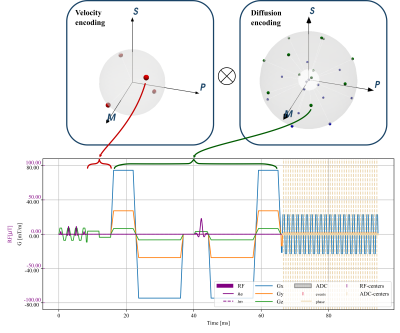
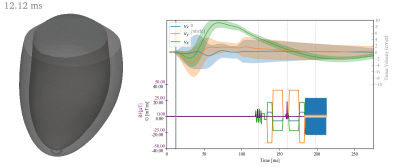
Starting from a spin-echo based cardiac DTI sequence with velocity and acceleration compensation (SE-M012)⁶, we defined a set of joint encoding gradient waveforms by inserting velocity encoding gradients according to the Hadamard scheme⁷. These velocity encoding gradients were placed into the delay between excitation and the start of the diffusion sensitization gradients. The available time was $$$6.9ms$$$ when using a 1-3-3-1 binomial excitation pulse with a field-of-view of $$$230\times97mm^2$$$ and a $$$2.35\times2.35 mm^2$$$ resolution (gradient limits of $$$80mT/m$$$ and $$$100T/m/s$$$). Figure 1 illustrates the velocity and diffusion encoding schemes with a VENC of $$$15 cm/s$$$ matching physiological tissue velocities up to $$$10 cm/s$$$^3-5. The b-value contribution of the velocity encoding gradients to diffusion encoding was below $$$1\%$$$. All sequence definitions were made using the CMRseq-framework (https://people.ee.ethz.ch/~jweine/cmrseq/latest/index.html).
Fig 2 illustrates a 3D left ventricular mesh model used as input and the sequence timings used for simulation with trigger delay of $$$40\%$$$ systole. For diffusion-weighted contrast simulation, the mesh was first refined to avoid inverse crime effects¹⁰ and subsequently a diffusion tensor was assigned to each node. Random sampling of smoothly varying diffusion tensors was used on a reference motion state⁸. Fiber motion and the corresponding tensor update were derived from the local mesh deformations (Fig 3).
The resulting signal for a diffusion weighted spin-echo experiment with single-shot readout including multiple coils was simulated with the CMRsim package (https://people.ee.ethz.ch/~jweine/cmrsim/latest/index.htm) assuming a separation of scale concerning diffusional and bulk motion. Hence, the moving particles were assumed to accumulate phase according to the discretized integration of $$$e^{j\gamma \int_0^{t} \mathbf{G}(t\prime)\mathbf{r}(t\prime)dt\prime}$$$ and magnitude attenuation depending on the diffusion tensor of the particle:
$$s(\mathbf{k}(t))=\left[\Sigma_i^j e^{2\pi\mathbf{k}(t)\mathbf{r}_i(t)}\ C_N(r)\ e^{b\mathbf{g}^T\mathbf{D_i}\mathbf{g}}\ e^{-\frac{|t-TE|}{T_2^{*}}}\ e^{j\gamma\Sigma_l^{T/\delta t}\mathbf{G}(l\delta t)\mathbf{r}_i(l\delta t)\delta t}\ e^{-\frac{TE}{{T_2}_i}}\ (1-e^{-\frac{T_{RR}}{{T_1}_i}})\ {m_0}_i\right]+\eta.$$
The simulation was evaluated for increasing trigger delays ($$$\tau$$$) from $$$35\%$$$ to $$$75\%$$$ of systole with an SNR of ~20. Subsequently, diffusion tensors were estimated from the magnitude images by solving:
$$\mathrm{arg}\min_{\hat{d}}\ |\mathbf{x}-B\hat{d}|^2_2$$with$$\mathbf{x}=[\log(s_1),\log(s_2),...],$$
where $$$s_i$$$ is the pixel-wise signal for all diffusion encodings composing the matrix $$$\mathbf{B}$$$. Tissue velocity per pixel was estimated using the Hadamard decoding matrix:
$$\vec{v}(\vec{r})=\frac{VENC}{\pi}\mathbf{D_v}\vec{\phi}(\vec{r}),\quad\mathbf{D_v}=pinv\begin{pmatrix}1&1&1\\1&-1&-1\\-1&1&-1\\-1&-1&1\end{pmatrix},$$
where $$$\vec{\phi}$$$ is the vector containing the four Hadamard encoded phases.
To evaluate errors in tensor and velocity estimation, three additional reference datasets were simulated using the same SNR and trigger delays:

• (i) no motion phase, without evaluation of the motion-phase operator in eq(1)
• (ii) ‘no venc’, full signal model without added velocity encoding
• (iii) ‘no diffusion’ no diffusion waveform and no magnitude attenuation

Diffusion metrics including mean diffusivity (MD), fractional anisotropy (FA), helix angle (HA) and absolute sheetlet angle (E2A) were calculated for simulated data (i), (ii) and the full signal model. Errors reported in Fig 4 correspond to using (i) as reference to (ii) and the full signal model. Tissue velocity estimation from jointly encoded data was compared to the estimation on (iii), which is shown in Fig 5.

Results and Discussion

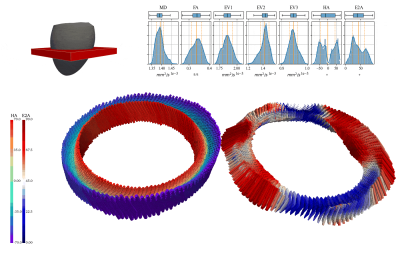
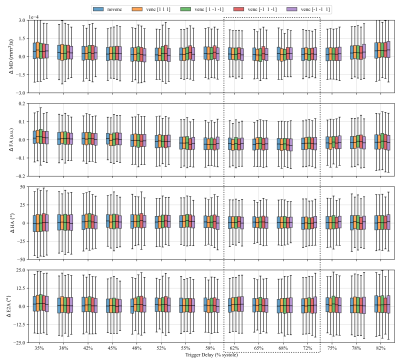
Figure 4 shows the effect of strain on the estimated diffusion tensors and hence the tensor metrics MD, FA, HA and E2A. The overestimation of MD at all trigger delays is consistent with expectations, as deformation results in intra-voxel phase gradients causing a reduced magnitude. Overestimation of FA in the early contraction phase is also expected as longitudinal strain (partially in fiber directions) is higher at the transition from iso-volumetric contraction to ejection as can be seen in Fig 2. HA and E2A are accurately estimated at trigger delays between $$$60\%-70\%$$$ systole (marked as dashed box in Fig. 4), which also reflects practical findings⁹. Errors vary only slightly between different velocity encoding directions, showing the negligible effect of the additional velocity encoding gradients.

Figure 5 shows the difference of estimated velocities for each diffusion weighting with respect to velocity encoding without diffusion weighting. Large deviations of velocity estimations occur for specific diffusion encoding directions at $$$450mm^2/s$$$, as phase wraps were not corrected before estimating the tissue velocity. Overall the interquartile range of velocity estimation errors are smaller than $$$3mm/s$$$ and the median is close to $$$0mm/s$$$ per spatial direction if phase-wraps are neglected which is approximately equal to $$$10\%$$$ of the changes of systolic longitudinal peak velocity for HCM patients⁴.

Conclusion

We have presented a concept of integrating systolic tissue velocity information within existing cDTI protocols. The method holds potential to provide further insights into the interplay of cardiac tissue motion and microstructure.

Acknowledgements