0331
Highly accelerated Cardiac CINE MRI using Neural Fields
Tabita Catalán1, Matías Courdurier1,2, Axel Osses1,3, René Botnar1,4,5, Francisco Sahli Costabal1,4, and Claudia Prieto1,4
1Millennium Nucleus For Applied Control And Inverse Problems, Santiago, Chile, 2Department of Mathematics, Pontificia Universidad Católica de Chile, Santiago, Chile, 3Department of Mathematical Engineering, Universidad de Chile, Santiago, Chile, 4School of Engineering, Pontificia Universidad Católica de Chile, Santiago, Chile, 5Institute for Biological and Medical Engineering, Pontificia Universidad Católica de Chile, Santiago, Chile
1Millennium Nucleus For Applied Control And Inverse Problems, Santiago, Chile, 2Department of Mathematics, Pontificia Universidad Católica de Chile, Santiago, Chile, 3Department of Mathematical Engineering, Universidad de Chile, Santiago, Chile, 4School of Engineering, Pontificia Universidad Católica de Chile, Santiago, Chile, 5Institute for Biological and Medical Engineering, Pontificia Universidad Católica de Chile, Santiago, Chile
Synopsis
Keywords: Image Reconstruction, Heart
Neural fields cardiac MRI (NF-cMRI), a method for highly accelerated CINE reconstruction using deep learning, is proposed. NF-cMRI relies on an intensity network, based on neural fields with Fourier features to encode a continuous reconstruction. The network is trained with one undersampled radial k-space data set without the need of a fully-sampled reference image. Good image quality of the heart is achieved with 8 radial spokes/cardiac frame. Results are compared against GRASP. Future work will focus on reducing reconstruction time and evaluating the proposed approach in prospectively undersampled k-space data.Introduction
Cardiac CINE MRI is the gold standard for cardiac functional assessment. However, spatial and temporal resolution is still limited since acquisition needs to be performed during one breath-hold (~15s). Several methods have been proposed that undersample the acquisition and exploit spatial-temporal redundancies to recover the non-acquired data 1,2. More recently deep-learning based undersampled reconstruction with unrolled neural networks have been proposed to further accelerate the scan 3. These models usually rely on convolutional neural networks (CNNs), generative models (GANs) or variational autoencoders architectures (VAE), which need to consider non-uniform FFT (NUFFT) for the case of non-Cartesian acquisition to reconstruct a discrete image in space and time. Here we propose an alternative approach for highly accelerated radial cardiac CINE MRI using neural fields (NF-cMRI), without the need of NUFFT. The proposed approach relies on an intensity network, based on neural fields with Fourier features 4, which is trained by comparing the predicted image and multiple-coil measured data in k-space using the continuous Radon transform. The proposed approach is trained independently for each undersampled dataset and does not require large datasets nor fully sampled reference for training.Methods
The proposed NF-cMRI approach relies on an intensity network (Intensity-Net), based on neural fields with Fourier features, which is trained by comparing the predicted image and multiple-coil measured data in k-space, using the continuous Radon transform (Fig.1). The Intensity-Net predicts the complex intensity value of the cardiac CINE images at spatial-temporal coordinate $$$(X,t)$$$. A neural field is simply a neural network whose input is a coordinate $$$x$$$, and whose output $$$\mathcal{N}(x;\theta)$$$ corresponds to the value of the image intensity at x. A multilayer perceptron (MLP) is trained to estimate the intensity of the reconstructed image in a given pixel, using the spatio-temporal coordinates $$$(X,t)$$$ of the pixel as input. An image is then generated by evaluating the MLP on a grid of points $$$\{X_{i,j},t_k\}_{i,j,k}$$$. A high dimensional mapping of the coordinates is used as input to the MLP, a technique called Fourier Features 4, to avoid the natural spectral bias of the MLPs 5, which learns first the low frequency components and can result in blurred images. Thus, a Gaussian Fourier Features is applied on the spatial coordinates, depending on two hyper-parameters: the mapping size $$$m$$$ and frequency gate $$$\sigma$$$, while the time coordinate is mapped to enforce periodicity.Training is done by comparing the k-space of the generated image with the acquired multiple-coil undersampled data using the Fourier-slice theorem, by calculating the FFT 1D of the Radon Transform of the generated image. For radial trajectories, comparison in k-space is usually done with NUFFT 6. Because of the continuous nature of Intensity-Net, here a rotation and interpolation are not necessary on the reconstructed image to calculate the Radon Transform; since the image can be evaluated directly in the rotated frame.The network is trained in one undersampled k-space data set without the need of a fully-sampled reference image. Reconstruction then corresponds with the training process; retraining is necessary to process a different data set.The proposed approach was evaluated in complex-value cardiac cine images with simulated multiple-coils and retrospective tiny golden radial undersampling. Acceleration factors of 13.3, 20, and 40 (w.r.t. fully sampled Cartesian), corresponding to 12, 8 and 4 radial spokes per cardiac phase, were studied. Results are compared against GRASP 6, using the BART 7 implementation.
Results and Discussion
Impact of Fourier Features hyper-parameters in the proposed NF-cMRI approach can be observed on Fig 2. Corresponding Structural Similarity Index Measure (SSIM) and Peak Signal to Noise Ratio (PSNR) in comparison to the fully-sampled referenced are also shown in Fig 2. Both parameters are used to control the band of frequencies that the Intensity-Net can learn. Small values of $$$\sigma$$$ result in blurred images. Based on those results, hyperparameters are chosen as $$$\sigma = 8.0$$$ and $$$m = 150$$$, and NF-cMRI is evaluated in comparison to GRASP for different numbers of radial spokes per frame. A spatial comparison can be seen in Fig 3, and a spatio-temporal one in Fig 4, whereas Fig 5 presents an animation of the reconstructed 2D CINE with the proposed NF-cMRI and GRASP for 8 spokes per frame. Both approaches show comparable results for 12 radial spokes/frame however blurring is introduced with GRASP for higher accelerations, whereas NF-cMRI achieves lower errors and comparable results to the fully sampled references for up to 8 radial spokes/frame.Conclusion
We have proposed a highly accelerated radial cardiac CINE MRI approach. The proposed NF-cMRI approach relies on an intensity network, based on neural fields with Fourier features, to achieve good image quality with 8 radial spokes/cardiac frame. The network is trained in one undersampled k-space data set without the need of a fully-sampled reference image. Future work will focus on reducing reconstruction time and evaluating the proposed approach in prospectively undersampled k-space data.Acknowledgements
This work was supported by the following grants:
- Millennium Nucleus for Applied Control and Inverse Problems ACIP NCN19_161
- Millennium Institute for Intelligent Healthcare Engineering ICN2021_004
References
- Lustig M, Donoho DL, Santos JM, Pauly JM. Compressed Sensing MRI. IEEE Signal Process Mag. 2008;25(2):72-82. doi:10.1109/MSP.2007.914728
- Pruessmann KP, Weiger M, Scheidegger MB, Boesiger P. SENSE: sensitivity encoding for fast MRI. Magn Reson Med. 1999;42(5):952-962.
- Hammernik K, Küstner T, Yaman B, et al. Physics-Driven Deep Learning for Computational Magnetic Resonance Imaging. Published online October 13, 2022. Accessed November 3, 2022. http://arxiv.org/abs/2203.12215
- Tancik M, Srinivasan P, Mildenhall B, et al. Fourier Features Let Networks Learn High Frequency Functions in Low Dimensional Domains. In: Advances in Neural Information Processing Systems. Vol 33. Curran Associates, Inc.; 2020:7537-7547. Accessed November 9, 2022. https://proceedings.neurips.cc/paper/2020/hash/55053683268957697aa39fba6f231c68-Abstract.html
- Rahaman N, Baratin A, Arpit D, et al. On the Spectral Bias of Neural Networks. In: Proceedings of the 36th International Conference on Machine Learning. PMLR; 2019:5301-5310. Accessed November 9, 2022. https://proceedings.mlr.press/v97/rahaman19a.html
- Feng L, Grimm R, Block KT, et al. Golden-angle radial sparse parallel MRI: combination of compressed sensing, parallel imaging, and golden-angle radial sampling for fast and flexible dynamic volumetric MRI. Magn Reson Med. 2014;72(3):707-717. doi:10.1002/mrm.24980
- Blumenthal M, Holme C, Roeloffs V, et al. mrirecon/bart: version 0.8.00. Published online September 24, 2022. doi:10.5281/ZENODO.7110562
Figures
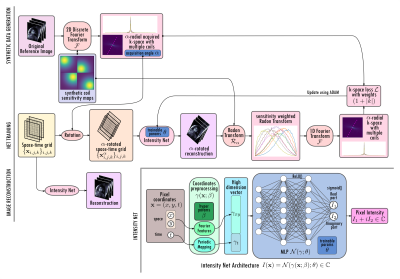
Figure 1: Diagram of the proposed NF-cMRI approach. Intensity Net is a coordinate-based MLP with a preprocessing step; Fourier Features is applied on the space coordinates, and a mapping on the time coordinate to enforce periodicity. Complex values are considered by using real and the imaginary part as output channels. A reconstructed image is then generated by evaluating the Intensity Net on a grid of points. The Radon transform is applied on the sensitivity-weighted generated image, and then compared to the golden-angle-sampled data with the 1D FFT and the Fourier Slice Theorem.
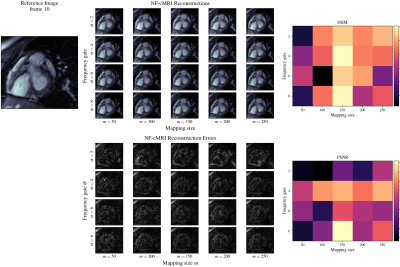
Figure 2: Impact of Fourier Features hyper-parameters on the proposed NF-cMRI reconstruction. No regularization is applied. Cropped versions of the reference and reconstructed images for 16 radial spokes/frame featuring the heart for a range of the hyper-parameters are shown, including the difference images w.r.t. the reference fully sampled image. Corresponding SSIM and PSNR are shown at the right.
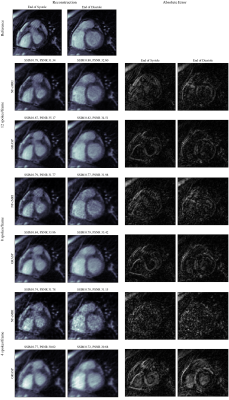
Figure 3: 2D CINE reconstructions (cropped around the heart for better visualization) using the proposed NF-cMRI and GRASP, with 16, 12 and 8 spokes/frame, and 320 samples/spoke, in comparison to the fully sampled reference image. End of systole and diastole frames are shown. Errors (difference images) for each plot are also included.

Figure 4: Temporal y-t cuts comparing reference, proposed NF-cMRI and GRASP. At higher undersampling, NF-cMRI shows less blurring compared to GRASP along the temporal axis.
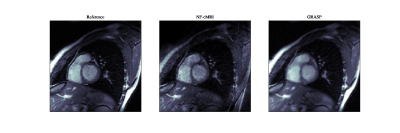
Figure 5 (Anim): Reconstructed 2D CINE with the proposed NF-cMRI and GRASP for 8 spokes per frame in comparison to the reference fully-sampled image.
DOI: https://doi.org/10.58530/2023/0331