0311
Multi-Coil Multi-Contrast Random Matrix Theory-Based Denoising for Liver Fat and R2* Quantification at 0.55T1Radiological Sciences, David Geffen School of Medicine, University of California Los Angeles, Los Angeles, CA, United States, 2Bioengineering, University of California Los Angeles, Los Angeles, CA, United States, 3Ming Hsieh Department of Electrical and Computer Engineering, University of Southern California, Los Angles, CA, United States, 4MR R&D Collaborations, Siemens Medical Solutions USA, Inc., Los Angles, CA, United States
Synopsis
Keywords: Low-Field MRI, Low-Field MRI
Liver fat and R2* quantification has been extensively validated at 1.5T and 3T. Recently, there is renewed interest in lower-field MRI because of potential advantages such as a larger bore and lower costs. However, it is challenging to acquire images with sufficient signal-to-noise ratio for accurate fat and R2* quantification at 0.55T. Previous random matrix theory (RMT)-based approaches leverage Gaussian noise characteristics to markedly reduce the noise without compromising the tissue signal. In this work, we investigated a multi-coil multi-contrast RMT-based denoising approach which is compatible with parallel imaging and we demonstrated improved liver fat and R2* quantification at 0.55T.
Introduction
Liver fat and R2* can be quantified using a multi-echo Dixon sequence followed by signal fitting to a model that resolves the fat spectrum and R2* 1-3. This approach has been extensively studied and validated at 1.5T and 3T1-3. In recent years, there is renewed interest in lower-field MRI (e.g., 0.55T) because of potential advantages such as a larger bore diameter and lower siting/hardware costs4-6. Previous studies investigated liver proton-density fat fraction (PDFF) and/or R2* quantification at lower fields7-9. However, it has been challenging to acquire images with sufficient signal-to-noise ratio (SNR) for accurate PDFF/R2* quantification. Recently, random matrix theory (RMT)-based denoising methods have been used in various MRI applications to improve image SNR10-12. RMT-based approaches leverage inherent Gaussian noise characteristics to markedly reduce the noise without compromising or smoothing the tissue signal10-12. Previous works on RMT denoising typically used datasets with large numbers of measurements/encodings or were performed in magnitude images only. Inspired by previous RMT denoising methods10-12, we investigated a multi-coil multi-contrast RMT-based denoising approach which can be compatible with parallel imaging and demonstrated its denoising capability for improving liver PDFF/R2* quantification at 0.55T.Methods
RMT-based denoising: RMT shows that if the additive noise in a dataset has zero-mean Gaussian distribution, the singular values of the noise matrices will follow the Marchenko-Pastur distribution as long as the number of data samples/measurements is large enough13. Based on RMT, a theoretical upper bound of these singular values can be estimated and used to specifically remove the Gaussian noise from the data.Several aspects need to be considered to apply RMT denoising in MRI images. First, sufficient number of data measurements is required to estimate noise characteristics. This limitation can be partially relieved by incorporating images from multiple coils and contrasts (e.g., multiple echo times). Second, parallel imaging is frequently used in clinical sequences. However, parallel imaging reconstruction can distort the noise characteristics and violate the noise assumptions in RMT.
Therefore, we used a reconstruction pipeline that allows us to apply RMT with parallel imaging (Figure 1). First, multi-coil multi-echo images were reconstructed using GeneRalized Autocalibrating Partially Parallel Acquisitions (GRAPPA), and divided by coil-by-coil g-factor maps14 to normalize noise characteristics. Second, the non-spatial dimensions were flattened into one dimension. Third, at each spatial location, a local patch with different coils and contrasts was extracted and flattened to a 2D matrix. Singular value shrinkage15 was performed using Marchenko-Pastur theory and the estimated noise variance. Fourth, multi-coil multi-echo images were scaled back by the coil-by-coil g-factor maps. Lastly, the multi-echo images were coil-combined16 and fitted to a 7-peak fat model with a single R2* term to generate PDFF and R2* maps17.
MRI Experiments: Two healthy subjects were scanned under an IRB-approved protocol, after providing written informed consent. Scans were performed using a whole-body 0.55T MRI system (prototype MAGNETOM Aera, Siemens Healthineers, Erlangen, Germany) equipped with high-performance shielded gradients (45 mT/m amplitude, 200 T/m/s slew rate). Phased-array receiver coils (18-channel spine array and 6-channel body array) were used. Data were acquired using a multi-echo gradient-echo 3D Cartesian sequence3. Key sequence parameters included TE=[2.16, 4.32, 6.48, 8.64, 10.8, 12.96]ms, TR=14.7ms, field of view=380x380mm2, slice thickness 5mm, and matrix size 192x192. Flip angle of 8° was used to balance between SNR and T1 bias for PDFF quantification. Parallel imaging factor R=2 was used for a single breath-hold acquisition (19 sec). For RMT denoising, a local patch size of 19x19x5 was used.
Results
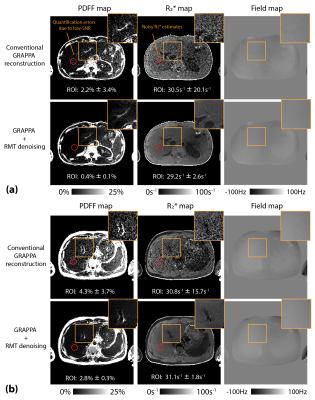
Figure 2 shows the denoising performance in each coil in both magnitude and phase images. The signal difference between RMT-denoised and original single-coil-channel images exhibited Gaussian-like noise. Figures 3 and 4 compare coil-combined multi-echo images reconstructed with and without RMT denoising. RMT denoising improved image SNR without smoothing the tissue features. Figure 5 shows the reconstructed PDFF, R2*, and B0 field maps using RMT denoising. Based on ROI analysis on the quantitative maps, RMT denoising can provide PDFF quantification with a lower bias and R2* measurements with substantially reduced standard deviation because of less noise (i.e., enhanced SNR).Discussion
Many previous RMT-based denoising methods only used coil-combined magnitude images11,12, which did not exploit the rich information across coils. Using the multi-coil information can increase the number of data samples by an order of magnitude to better comply with the RMT assumptions. In this work, we showed that if g-factor correction is not performed, the supposed noise removed by RMT denoising would deviate from a Gaussian distribution, increasing risk of removing or smoothing actual tissue signal. The proposed method makes RMT denoising compatible with parallel imaging acquisition and can be extended to different sequences and applications. It can especially benefit MRI applications at lower fields, which has a common fundamental challenge of low SNR. The performance of RMT denoising highly depends on the number of samples to accurately estimate the noise characteristics. In future work, we will investigate the required number of slices/contrasts for stable performance of RMT denoising.Conclusion
We demonstrated that multi-coil multi-contrast RMT denoising can be compatible with parallel imaging acquisition and improved liver PDFF and R2* quantification at 0.55T.Acknowledgements
We acknowledge grant support from the National Science Foundation (#1828736) and the National Institutes of Health (R01DK124417 and U01EB031894), and research support from Siemens Medical Solutions USA, Inc.References
1. Artz NS, Haufe WM, Hooker CA, Hamilton G, Wolfson T, Campos GM, Gamst AC, Schwimmer JB, Sirlin CB, Reeder SB. Reproducibility of MR‐based liver fat quantification across field strength: Same‐day comparison between 1.5 T and 3T in obese subjects. Journal of Magnetic Resonance Imaging 2015;42(3):811-817.
2. Armstrong T, Dregely I, Stemmer A, Han F, Natsuaki Y, Sung K, Wu HH. Free‐breathing liver fat quantification using a multiecho 3 D stack‐of‐radial technique. Magnetic resonance in medicine 2018;79(1):370-382.
3. Zhong X, Nickel MD, Kannengiesser SA, Dale BM, Kiefer B, Bashir MR. Liver fat quantification using a multi‐step adaptive fitting approach with multi‐echo GRE imaging. Magnetic resonance in medicine 2014;72(5):1353-1365.
4. Campbell-Washburn AE, Ramasawmy R, Restivo MC, Bhattacharya I, Basar B, Herzka DA, Hansen MS, Rogers T, Bandettini WP, McGuirt DR. Opportunities in interventional and diagnostic imaging by using high-performance low-field-strength MRI. Radiology 2019;293(2):384-393.
5. Wald LL, McDaniel PC, Witzel T, Stockmann JP, Cooley CZ. Low‐cost and portable MRI. Journal of Magnetic Resonance Imaging 2020;52(3):686-696.
6. Marques JP, Simonis FF, Webb AG. Low‐field MRI: An MR physics perspective. Journal of Magnetic Resonance Imaging 2019;49(6):1528-1542.
7. Campbell‐Washburn AE, Mancini C, Conrey A, Edwards L, Shanbhag S, Wood J, Xue H, Kellman P, Bandettini WP, Thein SL. Evaluation of Hepatic Iron Overload Using a Contemporary 0.55 T MRI System. Journal of Magnetic Resonance Imaging 2021;55(6):1855-1863.
8. Guenthner C, Koken P, Boernert P, Kozerke S. Three-point Dixon abdominal water/fat Separation using a lower-field 0.75T MRI. Proceedings of the 29th Annual Meeting of ISMRM; 2021.
9. Shih S-F, Cui SX, Zhong X, Tasdelen B, Yagiz E, Nayak KS, Wu HH. Free-breathing liver fat quantification using radial acquisition on a high-performance 0.55T MRI system. Processings of the 30th Annual Meeting of ISMRM; 2022.
10. Lemberskiy G, Baete S, Veraart J, Shepherd TM, Fieremans E, Novikov DS. Achieving sub-mm clinical diffusion MRI resolution by removing noise during reconstruction using random matrix theory. Processings of the 27th Annual Meeting of ISMRM; 2019
11. Veraart J, Fieremans E, Novikov DS. Diffusion MRI noise mapping using random matrix theory. Magnetic Resonance in Medicine, 2016;76(5):1582-1593.
12. Moeller S, Pisharady PK, Ramanna S, et al. NOise reduction with DIstribution Corrected (NORDIC) PCA in dMRI with complex-valued parameter-free locally low-rank processing. Neuroimage, 2021;226:117539.
13. Marčenko VA, Pastur LA. Distribution of eigenvalues for some sets of random matrices. Mathematics of the USSR-Sbornik, 1967;1(4):457.
14. Breuer FA, Kannengiesser SA, Blaimer M, Seiberlich N, Jakob PM, Griswold MA. General formulation for quantitative G‐factor calculation in GRAPPA reconstructions. Magnetic Resonance in Medicine, 2009;62(3):739-746.
15. Gavish M, Donoho DL. Optimal shrinkage of singular values. IEEE Transactions on Information Theory, 2017;63(4):2137-2152.
16. Walsh DO, Gmitro AF, Marcellin MW. (2000). Adaptive reconstruction of phased array MR imagery. Magnetic Resonance in Medicine, 2000;43(5):682-690.
17. Hernando D, Kellman P, Haldar JP, Liang, ZP. Robust water/fat separation in the presence of large field inhomogeneities using a graph cut algorithm. Magnetic Resonance in Medicine, 2010;63(1):79-90.
Figures
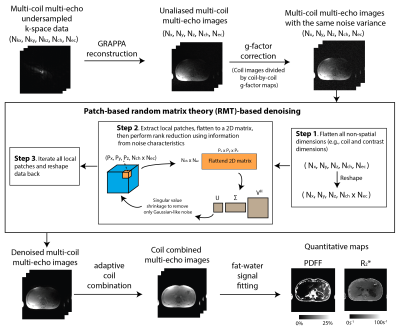
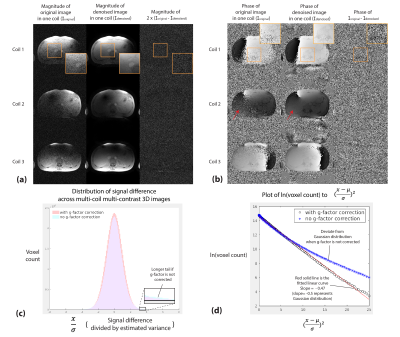
Figure 2. (a,b) Representative results comparing noise characteristics from g-factor-corrected coil images, images after RMT denoising, and their signal difference. Phase information, which is critical in fat-water separation, can be recovered in low-SNR regions (red arrows). (c) Histogram showing the distribution of the signal difference across the entire multi-coil multi-contrast images. (d) Signal difference compared to Gaussian-distributed signal. The signal difference deviates from Gaussian distribution if the g-factor was not corrected.
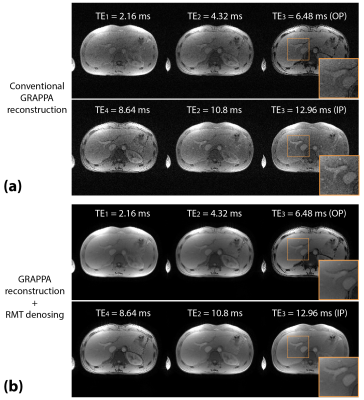
Figure 3. Example of reconstructed coil-combined 6-echo images from a 28-year-old male for (a) conventional GRAPPA reconstruction, and (b) GRAPPA reconstruction with RMT denoising. RMT denoising removed the Gaussian noise and improved image quality and sharpness in the multi-echo images. OP: out-of-phase; IP: in-phase.
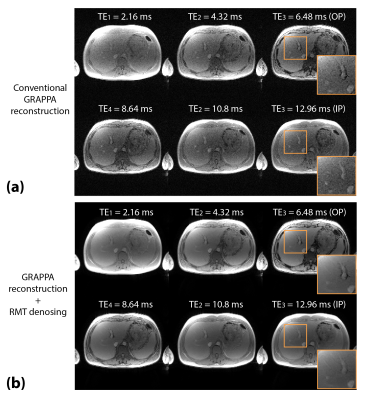
Figure 4. Example of reconstructed coil-combined 6-echo images from a 27-year-old male for (a) conventional GRAPPA reconstruction, and (b) GRAPPA reconstruction with RMT denoising. RMT denoising removed the Gaussian noise and improved image quality and sharpness in the multi-echo images. OP: out-of-phase; IP: in-phase.