0305
Accelerated Imaging at Ultralow Magnetic Fields: A comparative study of traditional and neural-network-based reconstruction approaches1Image X Institute, Faculty of Medicine and Health, The University of Sydney, Sydney, Australia, 2Department of Electrical Engineering and Computer Sciences, UC Berkeley, Berkeley, CA, United States, 3A. A. Martinos Center for Biomedical Imaging, Massachusetts General Hospital, Charlestown, MA, United States, 4Harvard Medical School, Boston, MA, United States, 5Department of Physics, Harvard University, Cambridge, MA, United States
Synopsis
Keywords: Low-Field MRI, Image Reconstruction
Portable MRI scanners that operate at very low magnetic fields are increasingly being deployed in clinical settings. However, accelerated acquisition and reconstruction methods that boost the quality of low-field MR images are needed to improve the diagnostic accuracy of the modality. Here, we compare leading data-driven and model-driven deep learning frameworks to compressed sensing (CS) for the reconstruction of undersampled ultralow field MRI data, finding that neural network approaches can boost quantitative image reconstruction metrics.
Introduction
Portable MRI scanners that operate at very low magnetic fields are increasingly being deployed in clinical settings.1 However, the intrinsic low signal-to-noise ratio (SNR) of these low-field MRI scanners often necessitates many signal averages, and therefore, excessively long acquisition times.2 Advanced reconstruction strategies based on deep learning could dramatically shorten acquisition times in low-field MRI when combined with undersampling.3 Here, we compare leading data-driven4 and model-driven5 deep learning frameworks to compressed sensing (CS) for the reconstruction of ultralow field MRI data, finding that neural network approaches can boost quantitative image reconstruction metrics.Methods
Our three-part study investigates the performance of different reconstruction methods on: (1) data sourced from the fastMRI database6 that simulates the transition from a high-field, high-SNR regime to a low-field, low-SNR regime, (2) experimental data acquired at 6.5$$$~$$$mT from a brain-shaped phantom7 and (3) ultralow field human brain data.Imaging experiments were performed on a 6.5 mT MRI scanner with a two-channel head coil.8 A 3D Cartesian balanced-steady state free precession (bSSFP) sequence with TR/TE = 22/11 ms and matrix size $$$64~\times~75~\times~25$$$ (Readout x Phase Encode 1 x Phase Encode 2) was used for acquisition with 32 signal averages. K-space was retrospectively 2$$$\times$$$ undersampled ($$$R~=~2$$$) in the phase-encode dimensions with a Poisson-disc (PD) mask. In the phantom experiment, a fully sampled acquisition with 256 averages was acquired as a ground truth. To generate a low-resolution dataset with high SNR, a high-resolution brain volume was extracted from the fastMRI database and downsampled to single-coil $$$64~\times~75~\times~25$$$ k-space data. This fastMRI k-space data was degraded through the addition of complex additive white Gaussian noise at varying noise power and then masked ($$$R~=~2$$$).
Data-driven AUTOMAP4 and model-driven Unrolled Optimization5 reconstruction networks were implemented as described in Refs 10 and 11, respectively. Briefly, the AUTOMAP network consists of 2 fully-connected layers and 3 deconvolutional layers that, through supervision, learns the spatial decoding process between k-space and image space without any prior knowledge. The Unrolling network incorporates known MR physics and, in our implementation, consists of 7 iterative soft shrinkage-thresholding blocks that each incorporate a data-fidelity term with forward and backward transforms that reduce image artifacts through convolutional operations. A training corpus of 50,000 brain image/k-space pairs sourced from the Human Connectome Project were used for network training with k-space data undersampled with a PD mask ($$$R~=~2$$$). To reconstruct 3D data, a 1D FFT was applied along the fully sampled readout dimension and trained networks were applied to the undersampled hybrid k-space.
For CS reconstruction, sensitivity maps were calculated with ESPIRiT,9 and L1-wavelet CS reconstruction was performed using SigPy.12 The regularization parameter ($$$\lambda$$$) was optimized for each reconstruction by performing a grid search over the range of [10-6,10-1]. As a baseline, images were also reconstructed via zero-filling and inverse fast Fourier transform (IFFT).
Normalized root-mean-square error (NRMSE) and structural similarity index (SSIM)13 metrics were calculated relative to a fully sampled ground truth acquisition. Metrics were also calculated after masking the region outside the head/phantom to exclude the effect of background noise.
Results
Undersampled fastMRI brain images were successfully reconstructed with the NRMSE of different reconstruction methods shown in Figure 1. At low SNR, Unrolling and AUTOMAP reconstruction methods outperform CS and IFFT techniques. CS gives the best NRMSE at high SNR. Comparing reconstructions for an input SNR of 60 dB in Figure 2, we find that background noise is strongly suppressed by neural-network reconstruction. After masking the background, we find CS and Unrolling metrics to be equivalent.Reconstructions of 2$$$\times$$$ undersampled phantom data are shown in Figure 3. Neural network approaches again suppressed background noise, with features better preserved in the Unrolling reconstruction. However, zero-filled IFFT and CS approaches gave the best metrics after background noise was masked.
Human brain images from a 22-minute scan are shown in Figure 4. Aliasing artifacts are present in all reconstructions of the 2$$$\times$$$ undersampled data. The Unrolling network appears to suppress noise within the brain itself.
Discussion
Undersampling is an effective means to shorten long MR acquisitions. Our findings demonstrate that AUTOMAP and Unrolling networks boost overall SSIM and NRMSE metrics when compared to traditional reconstruction methods. However, most of this performance boost comes from the suppression of background noise and as such, future work should focus on training neural networks to optimise metrics within the brain itself, which would further improve the clinical utility of low field MRI.14Unexpectedly, CS provided little performance benefit over zero-filled IFFT reconstruction for ultralow-field data. Likely, this limited performance benefit resulted from the very low SNR of the acquired data, indicating that the sampling pattern deployed could be tailored for acquisition at ultralow field.15,16
Conclusion
Our results demonstrate that Unrolling and AUTOMAP reconstruction methods boost NRMSE and SSIM metrics as compared to traditional CS and IFFT methods when reconstructing undersampled low-field data. Further, we have shown that CS remains a high-performing technique for the reconstruction of undersampled data at high SNR. Our findings will inform the development of faster imaging and robust reconstruction strategies for portable MRI.Acknowledgements
D.E.J.W. is supported by a Cancer Institute of NSW Early Career Fellowship 2019/ECF1015. The information, data, or work presented herein was funded in part by the Advanced Research Projects Agency-Energy (ARPA-E), U.S. Department of Energy, under Award Number DE-AR0000823. The views and opinions of authors expressed herein do not necessarily state or reflect those of the United States Government or any agency thereof. M.S.R. acknowledges the gracious support of the Kiyomi and Ed Baird MGH Research Scholar Award.References
1. Mazurek MH, Cahn BA, Yuen MM, et al. Portable, bedside, low-field magnetic resonance imaging for evaluation of intracerebral hemorrhage. Nat Commun. 2021; 12: 1-11.2. Wald LL, Mcdaniel PC, Witzel T, Stockmann JP, Cooley CZ. Low-Cost and Portable MRI. J Magn Reson Imaging. 2019; 49: e65-e77.
3. Ayde R, Senft T, Salameh N, Sarracanie M. Deep learning for fast low-field MRI acquisitions. Sci Rep. 2022; 12: 1-13.
4. Zhu B, Liu JZ, Rosen BR, Rosen MS. Image reconstruction by domain transform manifold learning. Nature. 2018; 555: 487-492.
5. Zhang J, Ghanem B. ISTA-Net: Interpretable Optimization-Inspired Deep Network for Image Compressive Sensing. Proc IEEE Comput Soc Conf Comput Vis Pattern Recognit. 2018: 1828-1837.
6. Knoll F, Zbontar J, Sriram A, et al. fastMRI: A Publicly Available Raw k-Space and DICOM Dataset of Knee Images for Accelerated MR Image Reconstruction Using Machine Learning. Radiol Artif Intell. 2020; 2: e190007.
7. Sarracanie M, Lapierre CD, Salameh N, Waddington DEJ, Witzel T, Rosen MS. Low-Cost High-Performance MRI. Sci Rep. 2015; 5: 15177.
8. Koonjoo N, Primavera B, Stockmann JP, Witzel T, Wald LL, Rosen MS. Quadrature Head Coil for Brain Imaging at 6.5 mT. In: 25th Meeting of the International Society of Magnetic Resonance in Medicine. Honolulu; 2017:2664.
9. Uecker M, Lai P, Murphy MJ, et al. ESPIRiT - An eigenvalue approach to autocalibrating parallel MRI: Where SENSE meets GRAPPA. Magn Reson Med. 2014; 71: 990-1001.
10. Koonjoo N, Zhu B, Bagnall GC, Bhutto D, Rosen MS. Boosting the signal-to-noise of low-field MRI with deep learning image reconstruction. Sci Rep. 2021; 11: 8248.
11. Shan S, Gao Y, Liu PZY, et al. Distortion-Corrected Image Reconstruction with Deep Learning on an MRI-Linac. arXiv. 2022: 2205.10993.
12. Ong F, Lustig M. SigPy: a python package for high performance iterative reconstruction. In: 27th Annual Meeting of the International Society of Magnetic Resonance in Medicine. ; 2019:4819.
13. Wang Z. Image Quality Assessment: From Error Visibility to Structural Similarity. IEEE Trans Image Process. 2004; 13: 600-612.
14. Sun L, Fan Z, Ding X, Huang Y, Paisley J. Region-of-interest undersampled MRI reconstruction: A deep convolutional neural network approach. Magn Reson Imaging. 2019; 63: 185-192.
15. Tamada D, Kose K. Two-dimensional compressed sensing using the cross-sampling approach for low-field MRI systems. IEEE Trans Med Imaging. 2014; 33: 1905-1912.
16. Schoormans J, Strijkers GJ, Hansen AC, Nederveen AJ, Coolen BF. Compressed sensing MRI with variable density averaging (CS-VDA) outperforms full sampling at low SNR. Phys Med Biol. 2020; 65: 0-13.
Figures
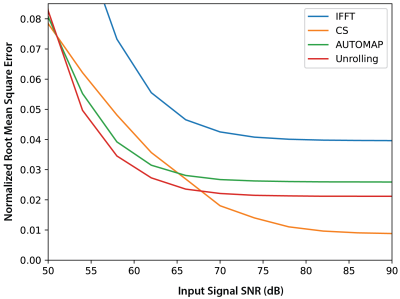
Figure 1: The normalized root mean square error (NRMSE) of images reconstructed from undersampled ($$$R~=~2$$$), low-resolution FastMRI k-space data at different input SNR values. The SNR of the input signal (k-space) was adjusted by adding synthetic Gaussian noise scaled to the ground truth k-space data. Zero-filled Inverse Fast Fourier Transform (IFFT) and Compressed Sensing (CS) approaches are compared to AUTOMAP and Unrolling network techniques.
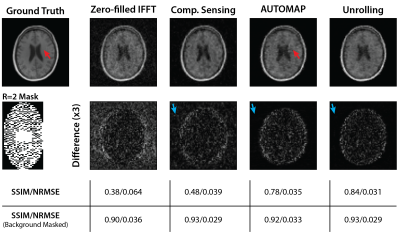
Figure 2: Reconstruction of low-resolution FastMRI data. Traditional and neural-network-based reconstruction techniques were used to reconstruct masked data ($$$R~=~2$$$) with additive white Gaussian noise (k-space SNR$$$~=~60~$$$dB). Blue arrows indicate the near complete suppression of background noise with AUTOMAP/Unrolling reconstruction as compared to CS. Red arrows indicate an artifact that has been enhanced in the AUTOMAP reconstruction.
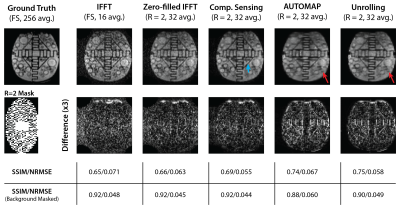
Figure 3: Reconstruction of ultralow field phantom data. Zero-filled IFFT, CS, AUTOMAP and Unrolling reconstructions are shown for a retrospectively masked ($$$R~=~2$$$) dataset. Images from an acquisition-time-equivalent scan with full-sampling (FS) and an IFFT reconstruction are also shown. The blue arrow indicates a sharp edge that is best recovered in the CS reconstruction. Red arrows indicate a region where details are better preserved in the Unrolling reconstruction than by AUTOMAP.
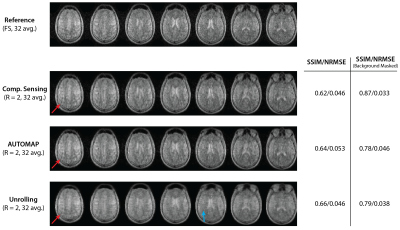
Figure 4: Images of the human brain acquired at 6.5$$$~$$$mT. Metrics for CS, AUTOMAP and Unrolling reconstructions of $$$R~=~2$$$ data are calculated against the fully sampled (FS, 22-minute) scan acquired with 32 averages. The central 7 of 25 slices are shown. Red arrows indicate aliasing artifacts present in all reconstructions due to undersampling. The blue arrow indicates a region in which a denoising effect most present in the Unrolling reconstruction can be observed.