0303
Four-fold acceleration of in vivo T1 mapping at 0.1 T using heavily-undersampled Look-Locker data and matrix completion1Center for Adaptable MRI Technology (AMT Center), Department of Biomedical Engineering, University of Basel, Allschwil, Switzerland, 2AMT Center, Institute of Medical Sciences, School of Medicine, Medical Sciences & Nutrition, University of Aberdeen, Aberdeen, United Kingdom
Synopsis
Keywords: Low-Field MRI, Relaxometry
Quantitative T1 mapping has proven useful in several clinical applications, nevertheless it is not widely deployed as it generally suffers from long acquisition times. This problem is exacerbated at low magnetic fields, due to inherent lower sensitivity. In spite of more favourable magnetisation properties (e.g., shorter recovery times, higher dispersion), exotic acquisition strategies and reconstruction pipelines are key to make quantitative MRI at low field fast, and compatible with clinical routines. Here, we present a low-rank matrix completion-based reconstruction method applied to heavily undersampled Look-Locker data for accelerated T1 mapping at 0.1 T.
Introduction
Quantitative MRI has proven valuable in neuro1,2, cardiac3, and MSK4 diagnosis and treatment follow-up. Recently it has been shown that specific biomarkers, like T1 contrast, can be unveiled at lower-than-conventional magnetic fields, due to the field dependence of tissue magnetic properties5,6 and the T1-enhanced dispersion at low magnetic fields7. Yet the employment of quantitative sequences at low field has been poorly explored, mainly because of their prohibitive acquisition times due to the high number of averages (NA) usually needed in low signal-to-noise ratio (SNR) regimes. Hence, strategies to accelerate scan time and to navigate through undersampling artifacts can play a crucial role to extend their deployment at low field.Here, a fast T1 mapping sequence that combines incoherent k-t-space sampling with a low-rank matrix completion-based reconstruction is presented. Preliminary results in doped water samples and in vivo are shown.
Methods
The proposed T1 mapping approach is based on a 3D Look-Locker (LL) inversion-recovery (IR) gradient recalled echo (GRE) sequence and consists of a preparatory inversion pulse, followed by a train of low-angle pulses α spaced by a time TRα. For each α-pulse, a different k-space line was acquired, following a random distribution, leading to an incoherent sampling pattern in the k-t domain (see Fig. 1a). A fixed 3×3 voxel calibration region, corresponding to the centre of k-space in both phase-encoding directions, was sampled at each time point. A low rank matrix completion reconstruction was employed to fill the k-space lines that were not acquired, taking advantage of the high correlation between the images acquired8.Five calibrated water samples were used to assess the robustness of the mapping method under heavy undersampling conditions. 125 images were acquired using a resistive biplanar MRI system (Bouhnik S.A.S., France) operating at 0.1 T and a custom solenoid RF coil. The sequence parameters were: α = 3°, matrix = 65×29×49, resolution = 2-mm isotropic, TR/TRα/TE = 2500/20/6 ms, bandwidth = 308 Hz/pixel. With only NA = 1 and 25% sampling (Fig. 1a), the whole acquisition took 14 min 49 s. A matrix size of 81×55×27 was employed to acquire in vivo T1 maps of a volunteer’s hand, leading to an acquisition time of 15 min 28 s. After matrix completion (Fig. 1b), the images were denoised using a BM4D filter9. T1 maps were then calculated performing a voxel-wise fit of the reconstructed images using the following variation of the conventional exponential recovery model10:
$$M_z(TR_{\alpha}) = M_0 \left[1+\beta T_1^*-(2+\beta T_1^*) e^{-\frac{TR_{\alpha}}{T_1^*}} +(1+\beta T_1^*) e^{-\frac{TR}{T_1^*}} \right],$$
with $$\beta = \frac{\log{(\cos{\alpha})}}{TR_{\alpha}}.$$
Here the fitting parameters are the equilibrium magnetisation M0 and the effective relaxation time T1*. A B1+ map acquired using the low-angle method11 was used as prior knowledge of the spatial distribution of the flip angle α. T1 was calculated from T1* using the following equation:
$$T_1 = \left(\frac{1}{T_1^*}+\beta\right)^{-1}$$
Results
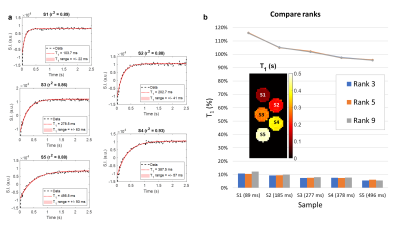
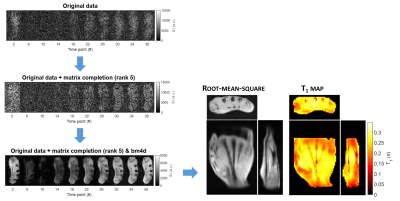
Fig. 2a shows the fitting of the signal intensity measured at the central pixel of each sample for a rank-5 reconstruction. Fig. 2b displays the central slice of the corresponding T1 map and compares the performance achieved when different ranks were used. The mean accuracy (lines) ranges between 116% (S1) and 95% (S5), while the intra-sample dispersion (bars) oscillates between 6% (S5) and 12% (S1). Both metrics show a T1-dependent trend. The three investigated ranks show comparable levels of performance. Fig. 3 outlines the processing pipeline employed for the in vivo data and compares the retrieved 3D T1 map with the root-mean-square of the images acquired at all time points.Discussion
A four-fold acceleration factor compared to a fully sampled k-t space was achieved with the proposed strategy. The high number of time points, combined with the presented post-processing steps, allowed navigation through the low SNR typical of the low-field regime, hence obviating the need for multiple averages. From the reconstructed images we could retrieve a robust T1 quantification in phantoms for a range of values comparable to those expected in the human body at 0.1 T. Fig. 2a shows that the first time point systematically deviates from the fit, possibly impacting more prominently the estimate of shorter T1s, where both accuracy and dispersion are worse. While at first sight this could be ascribed to an imperfect execution of the inversion pulse, further investigation is needed. In the absence of ground truth values, a reproducible choice of the rank is a crucial step to translate this method to clinical applications. Here we observed that the three explored ranks produced comparable results in the water samples. Nonetheless, the geometry of the chosen phantom might be too simple to exhaustively explore the pitfalls of the proposed mapping technique. Future developments are also envisioned for further acceleration. Given the T1 values measured in vivo, TR could be shortened by 30 % while still allowing full T1* recovery. A sparser k-t sampling could also accelerate the acquisition process.Conclusion
We have presented a fast T1 mapping method that compensates a heavy undersampling strategy with a low-rank matrix completion-based reconstruction. While a good quantitative accuracy was achieved, further refinement of the sampling strategy is required to make this technique compatible with clinical spatial and temporal resolutions.Acknowledgements
Swiss National Science Foundation Grant No. 170575.
Swiss National Science Foundation Grant No. 186861.
Swiss National Science Foundation Grant No. 198905.
References
1. Leandrou S, Petroudi S, Kyriacou PA, Reyes-Aldasoro CC, Pattichis CS. Quantitative MRI Brain Studies in Mild Cognitive Impairment and Alzheimer’s Disease: A Methodological Review. IEEE Rev Biomed Eng. 2018;11:97-111. doi:10.1109/RBME.2018.2796598
2. Granziera C, Wuerfel J, Barkhof F, et al. Quantitative magnetic resonance imaging towards clinical application in multiple sclerosis. Brain. 2021;144(5):1296-1311. doi:10.1093/BRAIN/AWAB029
3. Seraphim A, Knott KD, Augusto J, Bhuva AN, Manisty C, Moon JC. Quantitative cardiac MRI. J Magn Reson Imaging. 2020;51(3):693-711. doi:10.1002/JMRI.26789
4. De Mello R, Ma Y, Ji Y, Du J, Chang EY. Quantitative MRI musculoskeletal techniques: An update. Am J Roentgenol. 2019;213(3):524-533. doi:10.2214/AJR.19.21143
5. Bödenler M, Maier O, Stollberger R, et al. Joint multi-field T1 quantification for fast field-cycling MRI. Magn Reson Med. 2021;86(4):2049-2063. doi:10.1002/MRM.28857
6. Broche LM, Ross PJ, Davies GR, MacLeod MJ, Lurie DJ. A whole-body Fast Field-Cycling scanner for clinical molecular imaging studies. Sci Reports 2019 91. 2019;9(1):1-11. doi:10.1038/s41598-019-46648-0
7. Fischer HW, Rinck PA, van Haverbeke Y, Muller RN. Nuclear relaxation of human brain gray and white matter: Analysis of field dependence and implications for MRI. Magn Reson Med. 1990;16(2):317-334. doi:10.1002/mrm.1910160212
8. Doneva M, Amthor T, Koken P, Sommer K, Börnert P. Matrix completion-based reconstruction for undersampled magnetic resonance fingerprinting data. Magn Reson Imaging. 2017;41:41-52. doi:10.1016/j.mri.2017.02.007
9. Maggioni M, Katkovnik V, Egiazarian K, Foi A. Nonlocal transform-domain filter for volumetric data denoising and reconstruction. IEEE Trans Image Process. 2013;22(1):119-133. doi:10.1109/TIP.2012.2210725
10. Deichmann R. Fast High-Resolution T1 Mapping of the Human Brain. Magn Reson Med. 2005;54(1):20-27. doi:10.1002/mrm.20552
11. Balezeau F, Eliat PA, Cayamo AB, Saint-Jalmes H. Mapping of low flip angles in magnetic resonance. Phys Med Biol. 2011;56(20):6635-6647. doi:10.1088/0031-9155/56/20/00
Figures
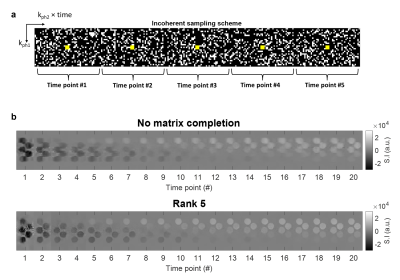
Incoherent sampling scheme and matrix completion in water samples. a) Example of the sampling matrix used to cover the k-t space. The white pixels indicate the acquired readout lines at the various phase-encoding steps. The yellow pixels define the calibration region. Only 5 of 125 time points are shown. b) Reconstructed real images (only the central slice is shown) for the first 20 time points. Top: applying the sole inverse Fourier transform. Bottom: matrix completion choosing rank 5.