0210
A 3D Surface Coil with Deep Learning Based Noise Reduction for Parotid Gland Imaging
Sayim Gokyar1, Chenyang Zhao1, Shajan Gunamony2,3, Jiaruo Yan2, Jonathan West4, Niels Kokot4, and Danny JJ Wang1,5
1USC Stevens Neuroimaging and Informatics Institute, Los Angeles, CA, United States, 2MR Coiltech Limited, Glasgow, UK, Glasgow, United Kingdom, 3Imaging Centre of Excellence, University of Glasgow, Glasgow, United Kingdom, 4Department of Otolaryngology - Head and Neck Surgery, LAC+USC Medical Center, Keck Medicine of USC, Los Angeles, CA, United States, 5Department of Neurology, Keck School of Medicine, University of Southern California, Los Angeles, CA, United States
1USC Stevens Neuroimaging and Informatics Institute, Los Angeles, CA, United States, 2MR Coiltech Limited, Glasgow, UK, Glasgow, United Kingdom, 3Imaging Centre of Excellence, University of Glasgow, Glasgow, United Kingdom, 4Department of Otolaryngology - Head and Neck Surgery, LAC+USC Medical Center, Keck Medicine of USC, Los Angeles, CA, United States, 5Department of Neurology, Keck School of Medicine, University of Southern California, Los Angeles, CA, United States
Synopsis
Keywords: New Devices, Neuro
Parotid salivary gland neoplasms occur in conspicuous locations near the facial nerve and have a risk for malignant transformation – making early diagnosis and treatment essential. Here we present a novel three-dimensional surface coil (3D Coil) architecture and a deep learning-based noise reduction method that offers twice higher signal to noise ratio compared to single channel surface coil for parotid gland imaging at 7T.Introduction
Malignant transformations of neoplasms in parotid glands can be diagnosed with MRI by using double echo state (DESS) sequence. Previous studies showed that ultra-high field (UHF) MRI (i.e.,>=7T) provides clear advantages over 3T in terms of better signal to noise ratio (SNR)1–4. However, different radiographers cannot agree with the trajectory of the facial nerves and parotid gland boundaries due to poor image quality and lower SNR levels. In this work, we address this problem by designing a 3D surface coil composed of single transmit element and three orthogonal receive elements combined by using deep learning methods5 to tackle lower SNR problem in the parotid region at 7T.Methods
Design and Simulations: The proposed 3D RF coil is composed of a circular Tx/Rx element (X-coil) with an effective diameter of 5.7 cm, an receive-only rectangular element (Y-coil) aligned perpendicular to the plane of X-coil, and a sniffer coil with a diameter of 2 cm aligned in parallel to the X-coil (Figure 1 a-c). We used Sim4Life6 and realistic body models (i.e., Duke and Ella) from the library of IT’IS7 to calculate the transmit pattern (B1+) of the 3D coil and receive patterns (B1-) of the three Rx elements. 3D coil design was manufactured by MR CoilTech Limited8. Final coil assembly was simulated at various locations such as face, neck, and leg for specific absorption rate (SAR) characterization.MRI Experiments: Proton resonance frequency (PRF) shift-based MR thermometry experiments were conducted at 7T Siemens Terra Scanner by scanning a gel phantom, using 6 mins long high-power RF signal, followed by GRE imaging (TR/TE:15/1.2ms, FA:15, FOV:128mm, Res:1mm isotropic) with phase reconstruction, repeated 6 times (total duration of 40 mins). Relative temperature increase was calculated by using the equations described before9. After obtaining local internal review board (IRB) approval, a volunteer was scanned by using DESS (TR/TE:14.2/5ms, FA:30, FOV:160mm, Res:0.4mm isotropic, TA:16:36) for assessing different image reconstruction methods, such as sum-of-squares (SoS)10, adaptive recombination11, and complex weighted reconstruction. In SNR calculations noise is predicted from intensity images by using a background region marked on figures.
Deep Learning: A three-channel deep learning architecture was designed (Fig. 1-d) with two cascaded convolutional neural networks (CNN) at the initial stage followed by single decoder/encoder stage. First CNN block was composed of 96 convolutional filters with a size of (3,3), an activation function of ‘relu’, and ‘He’ initialization. Contracted segment included the same block with 192 filters and half the pixel sizes. L2 loss function12 was used in connection with ‘Adam13’ optimizer. To train and test the network, an ACR MRI phantom was scanned with a previously defined GRE sequence, with 50 repetitions. Output images were used as the ground truths (GT) and repetitions were split by 40/5/5 for training/validation/test purposes. Trained network was then separately tested on a volunteer MRIs, acquired by using the DESS parameters given above with 5 repetitions (TA:47mins). Output images were used as the GT and DL network performance was tested by using SNR improvement and normalized root-mean-squared-error (NRMSE).
Results
Figure-2 compares the simulated receive performance of the single channel coil and the 3D coil in terms of receive field sensitivities(B1-). 3D coil achieved a 70% increase at a depth of 1-cm and 20% increase at a depth of 3-cm compared to single channel.Figure-3 depicts the simulation and experimental results of RF safety metrics. We have seen that the proposed coil may cause 10g averaged SAR of 4.1 W/kg for Duke body model. This was also validated on phantom experiment prior to IRB approval. We have observed a temperature increase of 0.5℃ after a 6 min heating sequence.
Figure-4 shows the performance comparison of different reconstruction methods such as SoS, adaptive, and complex combination (top row). We have seen that SoS, and complex recombination methods can achieve 30% SNR increase at 1 cm depth and 15% SNR increase up to 5 cm depths. Transverse slice (bottom right) of a complex recombination shows clear delineation of the parotid gland.
Figure-5 shows the DL-based image reconstruction from 3D Coil for 3 different slices. Acquiring the GT images took about 47 minutes, where the predictions were generated from single-repetition images with an acquisition duration of about 9mins and NRMSE of about 20%. Maximum predicted SNR levels are over twice higher than the single-channel SNR levels and slightly above the maximums of GT maps, showing the power of DL in noise suppression. Intricate details of the parotid mass as well as surrounding tissues were clearly delineated in the predicted SNR maps.
Conclusion
We have shown a proof-of-concept demonstration of a 3D surface RF coil utilizing a DL based noise reduction method to image the parotid gland at 7T. Multichannel Rx data was used to model background noise in DL network and generated MRIs with SNRs comparable to multi-repetition images with a reasonable scan duration.Acknowledgements
The authors are also grateful to Katherin Martin for the support during subject scanning, and John L. Go, and Liyang Tang from USC for useful discussions.References
1. Kraff O, Theysohn JM, Maderwald S, et al. High-resolution MRI of the human parotid gland and duct at 7 Tesla. Invest Radiol. 2009;44(9):518-524. doi:10.1097/RLI.0b013e3181b4c0cf2. Piludu F, Marzi S, Ravanelli M, et al. MRI-Based Radiomics to Differentiate between Benign and Malignant Parotid Tumors With External Validation. Front Oncol. 2021;11. Accessed November 1, 2022. https://www.frontiersin.org/articles/10.3389/fonc.2021.656918
3. Ban X, Hu H, Li Y, et al. Morphologic CT and MRI features of primary parotid squamous cell carcinoma and its predictive factors for differential diagnosis with mucoepidermoid carcinoma. Insights Imaging. 2022;13(1):119. doi:10.1186/s13244-022-01256-x
4. Freling N, Crippa F, Maroldi R. Staging and follow-up of high-grade malignant salivary gland tumours: The role of traditional versus functional imaging approaches – A review. Oral Oncol. 2016;60:157-166. doi:10.1016/j.oraloncology.2016.04.016
5. Kidoh M, Shinoda K, Kitajima M, et al. Deep Learning Based Noise Reduction for Brain MR Imaging: Tests on Phantoms and Healthy Volunteers. Magn Reson Med Sci. 2020;19(3):195-206. doi:10.2463/mrms.mp.2019-0018
6. Sim4Life by ZMT. Published November 2, 2022. Accessed November 5, 2022. https://zmt.swiss/sim4life/
7. Gosselin MC, Neufeld E, Moser H, et al. Development of a new generation of high-resolution anatomical models for medical device evaluation: the Virtual Population 3.0. Phys Med Biol. 2014;59(18):5287-5303. doi:10.1088/0031-9155/59/18/5287
8. MR Coiltech Limited, Glasgow, UK. Accessed November 1, 2022. https://www.mr-coiltech.co.uk/
9. Rieke V. MR Thermometry. In: Kahn T, Busse H, eds. Interventional Magnetic Resonance Imaging. Medical Radiology. Springer; 2012:271-288. doi:10.1007/174_2011_478
10. Larsson EG, Erdogmus D, Yan R, Principe JC, Fitzsimmons JR. SNR-optimality of sum-of-squares reconstruction for phased-array magnetic resonance imaging. J Magn Reson. 2003;163(1):121-123. doi:10.1016/S1090-7807(03)00132-0
11. Uecker M, Lai P, Murphy MJ, et al. ESPIRiT-an eigenvalue approach to autocalibrating parallel MRI: Where SENSE meets GRAPPA. Magn Reson Med. 2014;71(3):990-1001. doi:10.1002/mrm.24751
12. Zhao H, Gallo O, Frosio I, Kautz J. Loss Functions for Image Restoration With Neural Networks. IEEE Trans Comput Imaging. 2017;3(1):47-57. doi:10.1109/TCI.2016.2644865
13. Kingma DP, Ba J. Adam: A Method for Stochastic Optimization. Published online January 29, 2017. doi:10.48550/arXiv.1412.6980
Figures

Figure 1. (a) Visualization of parotid gland locations. (b) Schematics and placement of the proposed 3D Coil architecture on a realistic body model near parotid gland. (c) Coil composed of a circular Tx/Rx loop (X-coil), a rectangular Rx loop perpendicular to the Tx/Rx element (Y-Coil), and a sniffer coil on top of Y-coil for noise measurements. (d) Deep learning architecture for noise removal: input stage contains 96 convolutional features with a size of (3,3) followed by a down sampled layer containing 192 features.
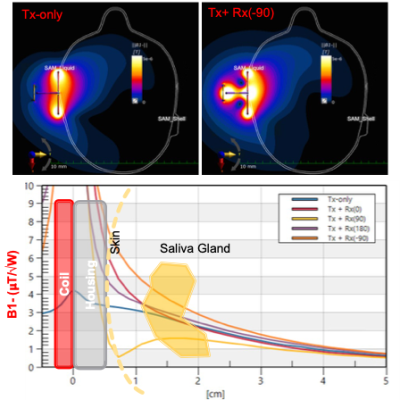
Figure 2. Comparison of receive sensitivity profiles for single-channel surface coil (Top left) and 3D coil (Top Right). The ratio of combined B1-fields to Tx-only case shows 70% increase at a depth of 1-cm and 20% increase at a depth of 3 cm for a phase shift of – 𝜋/2. Since the receive profile of the X- and Y-coils dominate the imaging volume (not the sniffer coil), their contribution to the final image was calculated by using different phase shifts. An optimal phase shift of – 𝜋/2 is observed due to their perpendicular alignment.
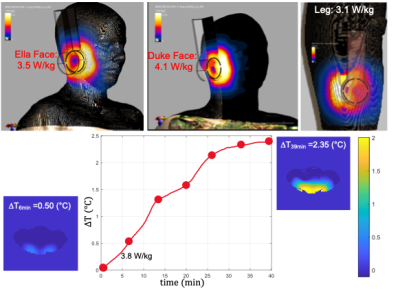
Figure 3. RF Safety analysis of the 3D coil is performed by using both Sim4Life and proton resonance frequency (PRF) shift-based MR thermometry. For a transmitted power of 1W, we have observed a 10 g average SAR value ranging from 3.1 to 4.1 W/kg. In a gel phantom study, we have observed a temperature increase of about 0.5℃ after a 6 min heating sequence. We calculated an average SAR of about 3.8 W/kg for the given experimental settings, which is quite in agreement with the simulation results.
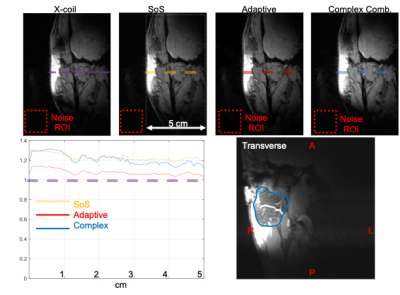
Figure 4. Performance comparison of different reconstruction methods are provided for the same coronal slice (top row). Although adaptive is very common in SENSE applications, it is not the best option here due to the overlap of coil sensitivity profiles. We have seen that SoS and Complex recombination method may offer 30% SNR increase at 1-cm depth and 15% SNR increase up to 5 cm, which is very useful for parotid gland imaging. Transverse slice (bottom right) of complex recombination shows clear delineation of the parotid mass. ROIs for noise calculation are given in dashed red rectangle.
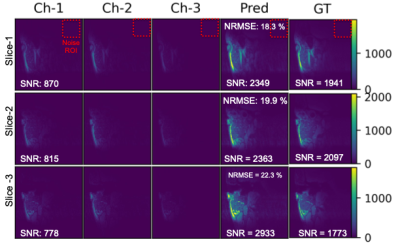
Figure 5. Deep Learning based image reconstruction from 3 channels (X-, Y-, and Sniffer Coils). Selection of 3 slices show the input images (Channels 1-3) and corresponding predictions (Pred.) of the DL network. Ground Truth (GT) images were generated from the SoS reconstructed slices with 5 repetition (TA of 47 minutes). Predictions from single repetition images (TA of about 9 mins) have NRMSE of about 20%. Maximum predicted SNR levels are higher than the GT maps, showing the power of DL in noise suppression. ROIs for noise calculation are marked on top row only.
DOI: https://doi.org/10.58530/2023/0210