0208
Online gradient optimisation for spokes parallel transmit – the BOGAT method1Wolfson Brain Imaging Centre, University of Cambridge, Cambridge, United Kingdom
Synopsis
Keywords: Parallel Transmit & Multiband, Parallel Transmit & Multiband
Spokes parallel transmit pulses improve the homogeneity of ultra-high field imaging. Typically the gradient trajectory (i.e. spoke kt-space positions) is determined using the iterative Fourier transform approach (FTA). We introduce “BOGAT” (Bayesian Optimisation of GrAdient Trajectory) to efficiently determine globally optimal gradient trajectories.
We evaluated BOGAT in phantoms for single-band and multi-band excitation, and retrospectively in 9 volunteers using existing B0 and B1+ maps.
BOGAT improves flip angle homogeneity (by 12.8% vs FTA, P<0.001) and reduces SAR (17.2%, P<0.001). Calculations take ~10s extra for a set of multiband pulses, making it feasible to use for online per-subject optimisation.
Introduction
Ultra-high field MRI can be limited by inhomogeneity (signal dropouts) and SAR. Parallel transmit (pTx) can in principle solve these challenges.Spokes pulses1 are popular slice-selective pTx pulses consisting of several RF subpulses separated by gradient blips. Typically 2-5 subpulses are used to minimise T2 losses. Several algorithms exist to optimise the subpulse RF coefficients to improve excitation flip-angle homogeneity and minimise SAR, including the popular Tikhonov-regularised Magnitude Least Squares (MLS) algorithm.2
Per-subject pulse optimisation requires this optimisation to complete while the subject lies still in the scanner, which is especially challenging when designing pulses for whole-brain slice-by-slice imaging. Therefore, it is common to select the gradient blips using fixed values or the simple iterative Fourier transform approach (FTA). Grid search approaches are not feasible online, even with enhancements such as sparsity enforcement.3 Local optimisation approaches such as greedy joint optimization4 are susceptible to getting stuck in local minima.
We introduce a new global optimization method Bayesian Optimisation of GrAdient Trajectory (BOGAT) for spokes pulse design using Bayesian Optimization5 and regularised Magnitude Least Squares (MLS). Bayesian Optimisation uses an acquisition function to express accumulating latent knowledge of the optimum gradient blips. It automatically and efficiently balances exploration and exploitation.
We evaluate BOGAT for designs of single slice and multiband spokes pulses in phantoms and in vivo.
Theory
With chosen spokes positions $$$\boldsymbol{\kappa}$$$, the optimal RF coefficients $$$\hat{\boldsymbol{b}}$$$ can be determined via regularised Magnitude Least Squares,2$$
\hat{\boldsymbol{b}} = \mathrm{argmin} \{ ||\,|\boldsymbol{A}(\boldsymbol{\kappa})\boldsymbol{b}| - \boldsymbol{m}_\mathrm{target}||^2 + \lambda ||\boldsymbol{b}||^2 \}.
$$
We repeat this optimisation with different spokes positions $$$\boldsymbol{\kappa}$$$ in an outer loop to find a joint RF and gradient optimum:
$$\hat{\boldsymbol{\kappa}} = \mathrm{argmin} \{ ||\,|\boldsymbol{A}(\boldsymbol{\kappa})\hat{\boldsymbol{b}}(\boldsymbol{\kappa})| - \boldsymbol{m}_\mathrm{target}||^2 + \lambda ||\hat{\boldsymbol{b}}(\boldsymbol{\kappa})||^2 \}.
$$
The cost function for $$$\boldsymbol{\kappa}$$$ is non-convex and slow to evaluate, so Bayesian Optimization is a suitable approach to find the global minimum. Our iterative algorithm is summarised in Figure 1c.
Methods
Grid searchA grid search was performed varying the kt-space position of the first spoke in a 2-spoke pulse. The kx-ky plane was sampled at 51x51 locations between ±0.15 cm-1. The final spoke was fixed at kx=ky=0. Calculations were performed using regularised MLS in the PTx Pulse Design toolbox (Siemens) with B0 and B1+ maps from a healthy volunteer.
Phantom validation
B0 and B1+ maps were acquired with dual-echo GRE and saturation-prepared TFL using an 8Tx32Rx head coil (Nova Medical) on a 7T Terra MRI (Siemens). PTx pulse optimizations used a modified version of Siemens’ pTx pulse design framework. A 2-spoke and a 3-spoke 90° pulse were designed for a single slice with BOGAT and a fixed 0.1 Tikhonov factor. For comparison, designs were repeated with Siemens’ default FTA spoke positioning (Figure 1d), with identical RF MLS optimization parameters.
The flip angle maps of these pulses were measured with a saturation-prepared TFL sequence with readout FA=5°, TR=5000ms, TE=1.85ms, 1.6mm*1.6mm in plane resolution. A linear correction was applied to the flip angle maps.6
Multiband design
Field maps were acquired as above for 3 slices 40 mm apart in the agar phantom. We applied BOGAT with a cost function weighted by seed points between all 3 slices. We compared to Siemens’ FTA method with spoke positions determined only by the central slice. RF coefficients were optimized with regularised MLS, with the Tikhonov factor determined by the L-curve method scaled down 1/2.
We measured MB FA maps in three separate scans. Each time magnetisation was prepared with the MB pulse, but readout was for a single slice each scan. The pulse energy was calculated for the modulated and summed MB pulse with optimized phase offset7.
In vivo validation
The same design methods were applied retrospectively for field maps from 9 healthy volunteers. We tested 45° excitation for MB2, MB3 and MB4 each with 36 sets of slice groups and 8 Tikhonov factors. Flip-angle RMSE was predicted using Bloch simulations.
Results and discussion
Figure 2 illustrates the cost function landscape of spoke positioning in a 2-spoke 30° pulse. The surface is generally smooth and non-convex. Tikhonov regularization does not significantly alter the cost function surface. Bayesian Optimisation is therefore appropriate.Figure 3 shows that Bayesian Optimization approximates the cost function closely (exploration) and converges to the global minimum (exploitation) within 50 iterations.
Figure 4a shows that for single slice pulse designs BOGAT achieves more homogeneous flip angle patterns (RMSE=12.9° and 8.6° for 2- and 3-spoke respectively; 29% and 55% decrease) than FTA (RMSE=18.1° and 19.4°).
Figures 4b shows that at a similar level of homogeneity, BOGAT reduces MB pulse energy in phantoms. Figure 5 shows similar benefits in healthy volunteers, with 17.2% mean energy reduction (P<0.001) and 12.8% RMSE reduction (P<0.001).
The mean total optimization time for a 2-spoke BOGAT MB3 pulse shows only a small increase from 13.7s to 22.8s compared to FTA. It achieves a global optimum spoke location with more than 50x speed up compared to a grid search.
Conclusions
We have developed a Bayesian optimization-based algorithm “BOGAT” for fast, global optimisation of spoke positions. Our method improves flip angle homogeneity compared to FTA method for both single slice and multiband excitations while decreasing pulse energy. Computation times are feasible for online per-subject optimisation.Acknowledgements
This research was supported by the NIHR Cambridge Biomedical Research Centre (BRC-1215-20014). The views expressed are those of the author(s) and not necessarily those of the NIHR or the Department of Health and Social Care. The Cambridge 7T MRI facility was co-funded by the University of Cambridge and the Medical Research Council (MR/M008983/1). M.Z. is supported by the Medical Research Council (MR N013433-1) and the Cambridge Trust. C.T.R. acknowledge Siemens for research support.
References
1. Setsompop, K. et al. Slice-Selective RF pulses for In-vivo B1+ Inhomogeneity Mitigation at 7 Tesla using Parallel RF Excitation with a 16-Element Coil. Magn Reson Med 60, 1422–1432 (2008).
2. Setsompop, K., Wald, L. L., Alagappan, V., Gagoski, B. A. & Adalsteinsson, E. Magnitude Least Squares Optimization for Parallel Radio Frequency Excitation Design Demonstrated at 7 Tesla With Eight Channels. Magnetic resonance in medicine 59, 908 (2008).
3. Zelinski, A. C., Wald, L. L., Setsompop, K., Goyal, V. K. & Adalsteinsson, E. Sparsity-Enforced Slice-Selective MRI RF Excitation Pulse Design. IEEE Trans Med Imaging 27, 1213–1229 (2008).
4. Ma, C., Xu, D., King, K. F. & Liang, Z.-P. Joint design of spoke trajectories and RF pulses for parallel excitation. Magnetic Resonance in Medicine 65, 973–985 (2011).
5. Jones, D. R., Schonlau, M. & Welch, W. J. Efficient Global Optimization of Expensive Black-Box Functions. Journal of Global Optimization 13, 455–492 (1998).
6. Tomi-Tricot, R. et al. Fully Integrated Scanner Implementation of Direct Signal Control for 2D T2-Weighted TSE at Ultra-High Field. in Proc. Intl. Soc. Mag. Reson. Med. vol. 29 0621 (2021).
7. Wong, E. Optimized Phase Schedules for Minimizing Peak RF Power in Simultaneous Multi-Slice RF Excitation Pulses. in Proc. Intl. Soc. Mag. Reson. Med. vol. 20 2209 (2012).
Figures
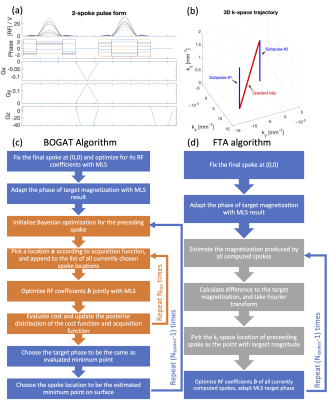
Figure 1 (a) RF and gradient form of a 2-spoke sinc pulse. (b) The transmit k-space (kt-space) trajectory of the 2-spoke pulse. (c) Our Bayesian Optimization of GrAdient Trajectory (BOGAT) algorithm for calculating the spokes trajectory, compared with (d) the automatic iterative Fourier transform-based approach (FTA) as implemented in Siemens PTx Pulse Design Framework.
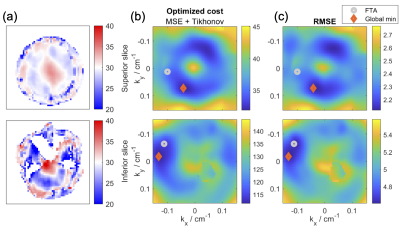
Figure 2 (a) The simulated flip angle map for a 2-spoke pulse designed with FTA in two slices with target flip angle 30°. (b) The cost function and (c) RMSE plot of the spokes position grid search of the first spoke in a 2-spoke pulse (2nd spoke fixed at kx=ky=0), in the corresponding slices. The global minimum spoke location and FTA spoke location are highlighted. Notice how the kt-space minimum (i.e. optimal spoke position or equivalently optimal gradient blips) are different for the superior and inferior slices, and FTA cannot consistently locate a minimum.
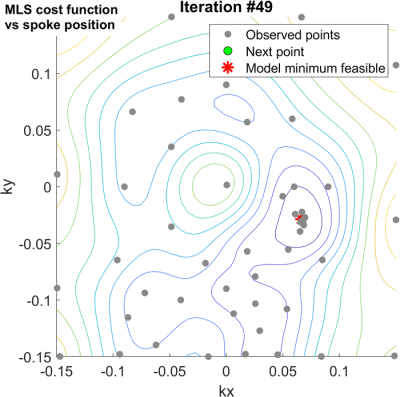
Figure 3 Animation of the Bayesian optimization Gaussian process mean estimation of the spoke position cost function surface as iterations progress. Calculated on one slice of in vivo field maps for a 2-spoke pulse. Kt-space coordinates denote that of the first spoke, with the second spoke fixed at kx=ky=0. Note the automatic balance between exploration (of unvisited area) and exploitation (around the visited the minima) allowing a good convergence within 50 iterations.
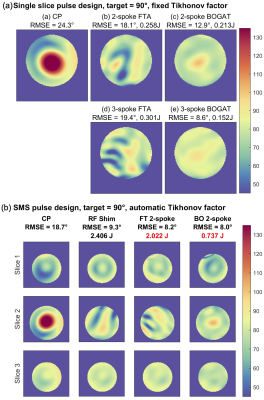
Figure 4 Phantom validation. a) Single slice 2- and 3-spoke flip angle map with FTA and BOGAT at a fixed Tikhonov regularization factor 0.1. BOGAT achieves more homogeneous excitation pattern in the agar phantom at a lower pulse energy. b) Flip angle maps and pulse energies for multiband factor 3 pulse designs. Automatic Tikhonov regularization factors determined with L-curve were used. Note the markedly lower pulse energy (55% reduction) when designed with BOGAT. All other MLS optimization parameters for RF coefficients were kept constant in all pTx methods.
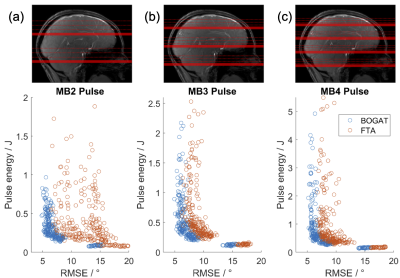
Figure 5 In vivo validation. The flip angle RMSE and pulse energy scatter plot of (a) MB2, (b) MB3 and (c) MB4 pulse designs with BOGAT and FTA, each with 36 sets of slice groups in 9 subjects. Pulses were designed as 2-spoke 45° excitation, time-bandwidth product 4.0, repeated with 8 different Tikhonov factors between 0.001 and 0.5. The better spoke location found by BOGAT shifts the L-curve to the left, reducing RMSE by 12.8% (P<0.001) and pulse energy by 17.2% (P<0.001) on average.