0202
A Versatile Toolbox for Rapid, Joint Design of pTx RF and Gradient Pulses Using Pytorch's Autodifferentiation1High Field MR Center, MPI for Biological Cybernetics, Tuebingen, Germany, 2Department for Biomedical Magnetic Resonance, University Hospital Tübingen, Tuebingen, Germany
Synopsis
Keywords: Parallel Transmit & Multiband, RF Pulse Design & Fields, Python, PyTorch, Optimization
Traditional pTx pulse design focuses on optimizing RF pulses with a fixed or parametrized gradient waveform. Utilizing fast GPUs for autodifferentiation, the optimization process becomes sufficiently efficient that RF pulses and the underlying gradient waveforms can be freely optimized concurrently within short time. This allows for the time-efficient creation of pTx pulses without prior knowledge about suitable gradient trajectories. Still, restrictions e.g. due to hardware limitations may be included into the optimization process.We provide a pulse design toolbox and demonstrate its ability to generate universal small-FA excitation pulses as well as large-FA pulses.
Introduction
State-of-the-art pTx applications optimize individual RF waveforms for multiple transmit channels, while applying gradient waveforms at the same time. Often this waveform is either predefined or derived from earlier optimization steps, in which a parameterized waveform was generated1,2. This had to be done to keep computational complexity manageable, in order to reduce calculation times.In more recent work gradient waveforms have been optimized either as a set of splines or completely freely together with a single RF waveform3,4.Modern optimization methods and ever-increasing computational power make free optimization of both parallel transmit pulses and gradient waveforms possible within reasonable time. Here we present a toolbox which uses PyTorch5, which was originally designed for machine learning, for simultaneous optimization of RF and gradient waveforms. PyTorch's autodifferentiation capabilities allow for automatic creation of jacobian matrices for functions with arbitrary complexity, which improves the performance of many optimization algorithms, thus reducing the required time for optimization.We present MPRAGE and GRE images acquired with a subject-specific tailored pulse (TP) which was optimized within approximately one minute. We also present universal pulses (UP) that were generated using this toolbox.
Methods
Software for pTx pulse optimization was developed in Python 3.9 using PyTorch 1.13.0. Local SAR supervision was performed using a Virtual Observation Points (VOP) model with 208 VOPs, which was specifically generated for this RF coil. All measurements were performed on a 9.4T whole-body MRI scanner (Magnetom 9.4T Plus, Siemens Healthineers, Germany) with 16 independent transmit channels, using a custom built head coil (16 transmit, 31 receive elements)6. Data was acquired from 14 healthy adults in accordance with the local ethics committee. $$$B_1^+$$$ and $$$B_0$$$ maps were acquired using 3D satTFL7 (TR=2.44 ms, TE=0.75 ms, GRAPPA 2x2, FA=2°/70°, matrix: 64x64x64, nominal resolution 3.5 mm isotropic).A full Bloch simulation taking $$$B_1^+$$$ and $$$B_0$$$ maps into account was implemented for arbitrary RF and gradient pulses. Additionally, the small tip angle approximation (STA) was implemented allowing for faster simulation of small tip angle RF pulses by using the spatial domain method8. Optimization of RF and gradient waveforms was performed using the AdamW algorithm. As it employs a gradient descent based method, the optimization greatly benefits from PyTorch's autodifferentiation capabilities. The learning rate was set to $$$4\cdot10^{-4}$$$ and the optimizer was reinitialized after every set of 1000 iterations, using the former set's best performing pulse as start value. The cost function used root mean square error (RMSE) and quadratic hinge functions of the system/SAR limits as metric. Optimization was run on a computer equipped with a NVIDIA RTX A6000 GPU (48GiB VRAM).
A pTx excitation pulse (FA=10°, SAR limit 2.3 W/kg, TR=25.5 ms, Pulse duration 520 µs, raster time 10 µs) was designed as UP on a database of 9 subjects and also as TP for 5 additional subjects. Optimization of all three gradient axes and 16 complex RF waveforms was run on the STA model for 2,500 iterations (TP) resp. 7,500 iterations (UP). The UP was then refined with 2500 iterations of the Bloch optimizer.The pulses were used in two imaging sequences, where they were scaled down to 9° (MPRAGE) resp. 5° (GRE) and compared to a CP mode pulse as defined by the MR scanner.
Furthermore, a pTx pulse with nominal flip angle of 90° was designed. This was done by optimizing a 9° pulse using 3500 iterations of the STA simulation. It was then scaled up by a factor of 10 and refined with 1000 iterations of the Bloch simulation. This pulse was designed without SAR constraint since it was only played out once, as preparation pulse for a satTFL sequence.
Results
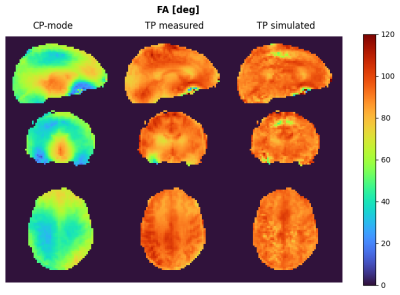
Calculation of the UP took 20.5 minutes for 9 subjects. When simulating the UP on the 5 subjects which were not part of the UP design database, the NRMSE to the target FA was (12.3±1.7)%.The tailored pulses for the same 5 subjects took approx. 67 seconds each to optimize and resulted in a NRMSE of (8.2±1.0)%. Figure 4 compares the FA distribution for all three pulses in one subject. It clearly shows that the CP-mode pulse not only has the widest FA distribution, but also misses the mean target FA of 10° by circa 40%.As expected the tailored pulse performs best, with a narrow FA distribution.
The large FA pulse took 3.5 minutes to optimize. In simulation it achieved an RMSE of 7.1%. The measured FA map is shown in Figure 5. It had an RMSE of 8.35%, compared to the CP-mode's RMSE of 39.58%. The mean FA was measured at 88.6°(TP) resp. 52.2°(CP).
Conclusion
We demonstrated that the new approach is faster, easier to implement and has more degrees of freedom than previous approaches. Tailored RF pulses for common imaging sequences can be designed rapidly. We designed a universal pulse which was successfully applied and showed that the simulation gives accurate results in the low- and high FA regime.Acknowledgements
Funding by the Deutsche Forschungsgemeinschaft (DFG –German Research Foundation) under the Reinhart Koselleck Programme (DFG SCHE 658/12) and by the European Research Council (ERC Advanced Grant No 834940, SpreadMRI) is gratefully acknowledged.References
1 Geldschläger, O., Bosch, D., & Henning, A. OTUP workflow: target specific optimization of the transmit k-space trajectory for flexible universal parallel transmit RF pulse design. NMR in Biomedicine. 2022; 35( 8):e4728. doi:10.1002/nbm.4728
2 Herrler, J., Liebig, P., Gumbrecht, R., Ritter, D., Schmitter, S., Maier, A., ... & Nagel, A. M. (2021). Fast online‐customized (FOCUS) parallel transmission pulses: a combination of universal pulses and individual optimization. Magnetic resonance in medicine, 85(6), 3140-3153. doi:10.1002/mrm.28643
3 Hao, S., Fessler, J. A., Noll, D. C., & Nielsen, J. F. (2015). Joint design of excitation k-space trajectory and RF pulse for small-tip 3D tailored excitation in MRI. IEEE transactions on medical imaging, 35(2), 468-479. doi:10.1109/TMI.2015.2478880
4 Luo, T., Noll, D. C., Fessler, J. A., & Nielsen, J. F. (2021). Joint Design of RF and gradient waveforms via auto-differentiation for 3D tailored excitation in MRI. IEEE Transactions on Medical Imaging, 40(12), 3305-3314. doi:10.1109/TMI.2021.3083104
5 Paszke, A., Gross, S., Massa, F., Lerer, A., Bradbury, J., Chanan, G., ... \& Chintala, S. (2019). Pytorch: An imperative style, high-performance deep learning library. Advances in neural information processing systems, 32. doi:10.48550/arXiv.1912.01703
6 Shajan G., Kozlov M., Hoffmann J., Turner R., Scheffler K., & Pohmann R. A 16-channel dual-row transmit array in combination with a 31-element receive array for human brain imaging at 9.4 T. Magnetic Resonance in Medicine. 2013;71(2):870–879. doi:10.1002/mrm.24726
7 Bosch, D., Bause, J., Geldschläger, O., & Scheffler, K. Optimized ultrahigh field parallel transmission workflow using rapid presaturated TurboFLASH transmit field mapping with a three-dimensional centric single-shot readout. Magn Reson Med. 2023; 89: 322- 330. doi:10.1002/mrm.29459
8 Grissom, W., Yip, C. Y., Zhang, Z., Stenger, V. A., Fessler, J. A., & Noll, D. C. (2006). Spatial domain method for the design of RF pulses in multicoil parallel excitation. Magnetic resonance in medicine, 56(3), 620-629. doi:10.1002/mrm.20978
Figures
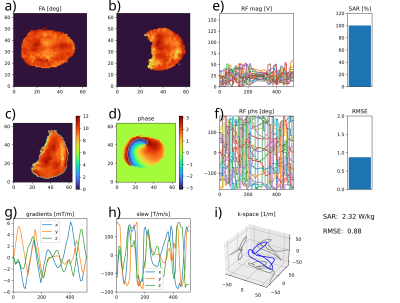
Figure 1: Optimization result of a 10° pTx pulse with a duration of 520 µs. The optimization took 66 seconds. Subplots a-c) display the simulated FA, subplot d) the resulting phase. Subplots e-f) show the RF magnitude and phase for each channel. The gradient waveforms and the corresponding slew rates and k-space trajectories can be seen in subplots g-i).
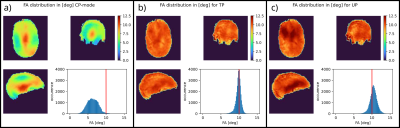
a) CP-mode pulse as calculated by the MR-Scanner. Note how the median FA misses the target by approximately 40%.
b) Tailored pulse optimized for this specific subject. The FA distribution is narrow and the histogram peak is on target.
c) Universal pulse optimized on a database of 9 other subjects. The FA distribution is wider than for the tailored pulse, but the UP still clearly outperforms CP-mode.