Synopsis

Keywords: Myocardium, Perfusion

As an alternative to Gadolinium, metabolically inert hyperpolarized contrast agents have been used in perfusion studies. For myocardial perfusion measurements, it is challenging to reliably obtain perfusion-related signals due to partial volume effects. We propose a constrained decomposition approach, enforcing prior knowledge of the residue function being temporally decreasing. The method is capable of separating the arterial and perfusion components and the quantified perfusion map is not visibly affected by partial volume effects.

Introduction

Metabolically inert hyperpolarized contrast agents have been used in myocardial perfusion studies. However, myocardial perfusion quantification remains challenging: The myocardial signal is contaminated by the 100-fold higher neighbouring left ventricle(LV) signal due to partial volume effects. Some previous studies have addressed this by suppressing the LV signal using velocity selective RF¹ or flow sensitising gradients². We propose a constrained decomposition method to separate the right/left ventricle and myocardium signals. The proposed method is tested and compared with constrained truncated SVD (TSVD) (representative of state of the art)^3,4 on simulated and in vivo data.

Methods

The method can be mathematically formulated as follows:
$$Given \;\mathbf{H}:
\min _{\boldsymbol{W}}\|\mathbf{X}-\mathbf{W H}\|, \;subject \;to \;\mathbf{W}>0$$
$$
Given \;\mathbf{W}:
\min _{\boldsymbol{H}}\|\mathbf{X}-\mathbf{W H}\|, \;subject\;to \;\mathbf{G R}>0$$
Here, $$$ \mathbf{R}$$$ is the vectorized residue function given by the tissue tracer concentration $$$ \mathbf{H_{perf}}$$$ deconvolved with the arterial input $$$ \mathbf{H_{AIF}}$$$, and $$$ \mathbf{G}$$$ is the derivative operator. The data $$$ \mathbf{X} \in \mathbb{R}^{m \times n}$$$ is approximated by a product of $$$ \mathbf{W} \in \mathbb{R}^{m \times c}$$$ and $$$ \mathbf{H} \in \mathbb{R}^{c \times n}$$$, m is the number of voxels, c is the number of components and n is number of time points. Matrix $$$ \mathbf{H}$$$ contains component time courses and $$$ \mathbf{W}$$$ are weights. The approximation is improved by iteratively solving two constrained least squared (LS) error problems. First solving for $$$ \mathbf{W}$$$ given $$$ \mathbf{H}$$$. Elements in $$$ \mathbf{W}$$$ are constrained to positive values. Second LS problem is solving for $$$ \mathbf{H}$$$ given $$$ \mathbf{W}$$$. The residue function is known to be monotonically decreasing, so this is enforced as a constraint. It is calculated as the tissue tracer signal deconvolved by the AIF using a TSVD method.

Simulation
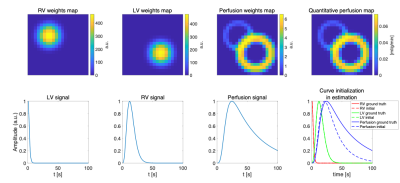
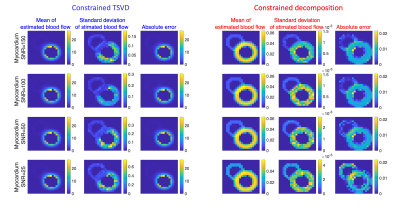
Myocardial perfusion MRI time series are simulated for validation (right/left ventricle and myocardium). Their chosen weight maps and concentration time curves are shown in Figure 1. The perfusion signal weights are scaled down to 1/100 of LV weights. To simulate partial volume effects, the weight maps are smoothed. The MR signal is calculated by multiplying the weights with component curves before noise is added. For perfusion estimation, Monte Carlo simulation is performed to compare constrained TSVD^3,4 with the proposed method, where the weights are initialised as zero and the component curves are initialised as shown in Figure 1. Four different myocardium SNR levels with gaussian noise are simulated and for each, the estimation is repeated 20 times with different noise realizations. The estimate’s mean and standard deviation are calculated for each SNR level and method.

Animal handling
Two healthy 40 kg female Danish domestic pigs participated and were handled as described in reference⁵. Cardiac stress was pharmacologically induced by continuous intravenous infusion(600ml/h) of adenosine(5mg/ml) and dobutamine(12.5mg/ml) in saline. Imaging started 3 minutes into the stress infusion.

Hyperpolarization and in vivo datasets
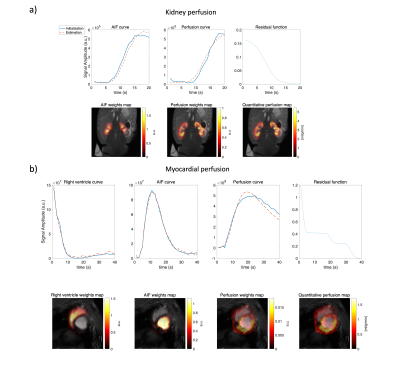
Pyruvate and HP001 were hyperpolarized using the dynamic nuclear polarization method. The pyruvate sample preparation is described in reference⁶. 300uL HP001 with 40 mM trityl radical was polarised with a SpinAligner(Polarize, Denmark), and dissolved into 15 ml saline providing 166mM HP001 solution. The method was tested with two in-vivo porcine datasets: Pyruvate images were obtained from a single slice in the coronal plane of the kidney using a dynamic 2D spectral-spatial excitation with a spiral readout. In another pig, myocardial HP001 images were acquired under stress with a 3D gradient echo stack-of-spirals sequence in the short axis view with diastolic gating.

Result and Discussion

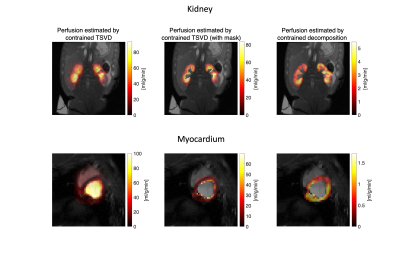
The simulation setup and results are shown in Figure 1 and 2. The absolute error and standard deviation of the constrained decomposition method is 10 times smaller than the constrained TSVD method (Figure 2). Figure 3 shows the performance in vivo. In both, the proposed method can separate perfusion and AIF components. Figure 4 shows the in vivo comparison of the two methods. In both in vivo cases, the perfusion estimated by constrained TSVD is higher near the arteries compared to the proposed method. The normal perfusion values in a pig are around 3ml/g/min in the kidney and 2 ml/g/min in the myocardium^7,8. Compared to the reference value, the constrained TSVD method has a perfusion value of around 80 ml/g/min near the arterial characterized by the AIF component, whereas the proposed method has a perfusion value of around 4 ml/g/min. So far, the proposed method is only designed and tested for healthy myocardium described by a single signal component. For myocardial ischemia, several myocardial components may need to be added and constrained, to sufficiently describe variation in bolus arrival timing.

Conclusion

Constrained decomposition can separate perfusion and arterial signal components, reducing partial volume effects. Compared to the proposed method and reference values, the constrained TSVD method overestimated perfusion near the arterial region. So far, the proposed method has only been tested for healthy myocardium. More components are needed to model variation in the shape of the residue function, e.g expected for myocardial infarction.

Acknowledgements

No acknowledgement found.