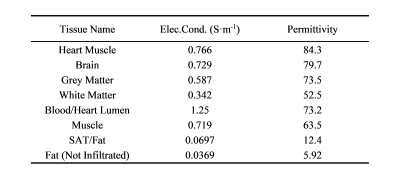Introduction

The issue of safety risks for patients wearing active implantable medical device (AIMD) undergoing magnetic resonance imaging (MRI) examinations has been a long-standing concern. A four-Tier approach is proposed in ISO/TS 10974¹ to assess the heating of the tissue surrounding the implant, with the Tier-3 and Tier-4 approaches being suitable for AIMDs with long electrical lengths. Whereas there are still many limitations or simplifications when performing these methods. Tier-4 approach requires full-wave electromagnetic modelling of implant, human and radiofrequency (RF) coil, which is notoriously time consuming and high-powered computing clusters is needed². Tier-3 transforms tangential incident E-field into the temperature rise of the tissue near the implant electrode by means of the implant's RF transfer function. However, the current mainstream methods for measuring transfer function greatly simplify the human tissue in the vicinity of the implant and use a homogeneous simulation fluid as a substitute^3-5, thus AIMDs with relatively complex implant environments are not suitable for these methods in most cases. More importantly, both Tier-4 and the current methods for measuring transfer functions can only be evaluated on a case-by-case basis for each implant, which can be quite time-consuming.

With these problems in mind, we propose machine learning algorithms that can predict the RF transfer function of AIMDs both in homogeneous and heterogeneous environments based on their geometric parameters and tissue distribution around the AIMDs. In this way, not only a rapid and effective assessment of the RF transfer function can be completed, but the impact of the complicated tissue environment on the transfer function is also taken into accounts in the assessment process.

Method

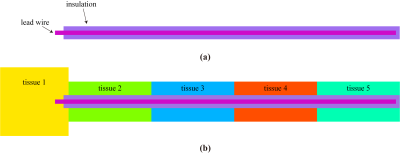
A generic AIMD model was constructed as shown in Figure 1(a), several AIMD models with different geometrical parameters of length 400~700 mm (step: 50mm), electrode length 1~5 mm (step: 1 mm), lead wire radius 0.1~0.4 mm (step: 0.1 mm), and insulation thickness 0.1~0.4 mm (step: 0.1 mm) were generated. In addition, in the case of heterogeneous, the tissue was modeled at 10 cm intervals along the length of the implant (3 cm at the tip of the electrode), as shown in Figure 1(b).

Finite-difference time domain (FDTD) simulations were performed in Sim4Life v7.0 (ZMT Zurich MedTech, Zurich, Switzerland) to model the RF transfer function of the AIMD. Unlike the conventional method of measuring the transfer function by piece-wise excitation, we set up a hard current source near the implant electrode based on the reciprocity principle⁵ and current sensors were placed at 5 mm intervals around the implant to capture the current distribution and obtain the transfer function. In the homogeneous circumstance, the phantom was modeled as tissue material with conductivity of σ = 0.4~1.2 S/m (in steps of 0.2 S/m), and permittivity of ε_r = 10~80 (in steps of 10). In the heterogeneous case, each segment of tissue as shown in Figure 1(b) was set to a randomly generated tissue category from Table 1. The operating frequency was at 128 MHz for 3T MRI. Wave number k and input impedance Z are used to fit the transfer function curve S(l), the formula is as follows⁶:
$$S(l)=C\cdot(i/2Z)\cdot\frac{sink(L/2-l)}{cosL/2}$$
where C is a constant factor, and L is the length of AIMD.

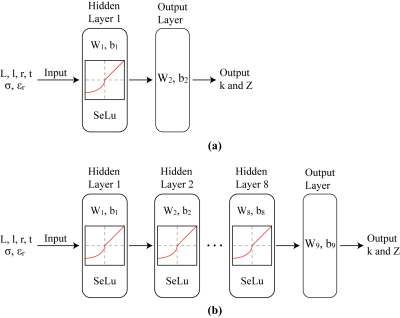
As shown in Figure 2, feedforward neural networks based on Keras sequential⁷ were designed for homogeneous and heterogeneous cases. The 532 homogeneous scenarios and 592 heterogeneous scenarios were divided randomly into training set (60%), validation set (20%), and testing set (20%), respectively. AIMD length L, electrode length l, lead wire radius r and insulation thickness t, as well as the conductivity σ and permittivity ε_r of tissues are used as the inputs for the neural network. The output would be wave number and input impedance. Predictive performance was evaluated with the correlation coefficient (R), the SeLu activation functions were used in the hidden layers. Batch normalization is applied to solve the problem of covariance shift. Hyperparameter optimization was conducted using SGD⁸ in homogeneous network and Adam⁹ in heterogeneous network.

Results

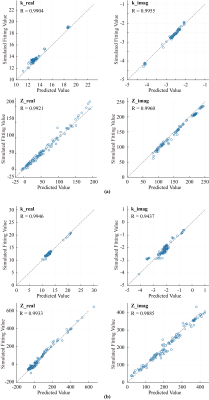
Figure 3(a) shows the performance of the proposed machine learning algorithm in predicting k and Z from geometrical parameters of AIMD and electronic parameters of tissue in homogeneous tissue environments.

From the results, the designed algorithm is able to predict well for k and Z, testing performance is indicated with an average R ≈ 0.99. And Figure 3(b) is for heterogeneous tissue environment, with an average R ≈ 0.98.

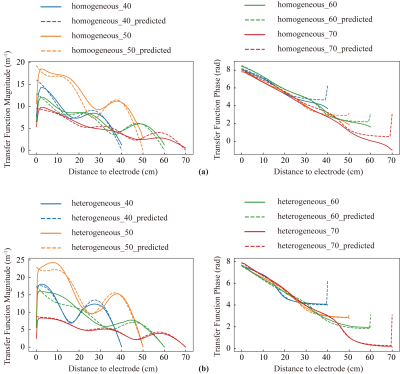
Comparison of predicted and simulated transfer functions for lengths of 40 cm, 50 cm, 60 cm, and 70 cm in homogeneous and heterogeneous tissue environment is shown in Figure 4.

Conclusion

A machine learning-based evaluation method has been proposed in this study to enable a rapid and accurate prediction of the AIMD transfer function. As a preliminary study, the results show that the proposed method can be used as an alternative to traditional numerical and experimental transfer function assessment. With the proposed approach, inherent disadvantages of numerical simulations (e.g., expensive computational cost) and experimental measurements (e.g., limitation in measuring under heterogeneous tissue conditions) may be overcome. Moreover, the proposed approach can be applied to both homogeneous and heterogeneous implantation scenarios, allowing a more flexible implementation under different clinical tissue environments.

Acknowledgements

This work was supported by National Natural Science Foundation of China (Grant No.6210010061). The authors would like to thank Zurich MedTech (ZMT, Zurich, Switzerland) for providing Sim4Life for scientific use.