Synopsis

Keywords: Machine Learning/Artificial Intelligence, Machine Learning/Artificial Intelligence

We propose MRFlow, which is a normalizing flow-based neural network for the MRI harmonization framework. With the normalizing flow trained only with the target domain (e.g., 3T image) data, we harmonize the image from the source domain (e.g., 1.5T image) to the target domain by alternately reducing the norm of the latent variable and increasing similarity between the source domain and harmonized images. When MRFlow is applied to synthesized source domain images, the harmonized images showed lower errors than the source domain images. In the prospective study, the harmonized images became more similar to the target domain images after MRFlow.

Introduction

Although deep learning-based MR image methodologies have been widely developed,^1,2 variations of MR images across vendors, scanners, and scan parameters have raised a generalization issue of deep learning.³ To overcome such generalization challenges, harmonization methods that match the image of the source domain (e.g., 1.5T image) to the target domain (e.g., 3T image) have been developed by utilizing end-to-end UNet⁴ or CycleGAN-based style transfer.^5,6 Despite noticeable performances, however, these methods have a limitation in that they have limited accuracy when applied to an unseen domain. Recently, a neural network named the normalizing flow was introduced and showed great performance in diverse computer vision tasks.^7,8 Normalizing flow can learn the prior of image distribution with the invertible network. In this study, we utilized this normalizing flow to harmonize MR images from a domain that has not been trained in the model.

Methods

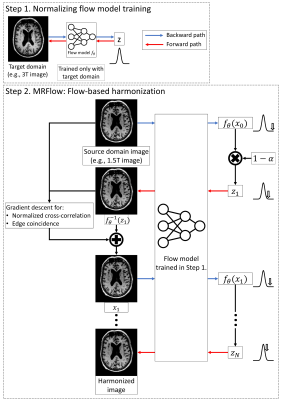
[Normalizing flow] The goal of the normalizing flow is to learn an invertible mapping $$$f$$$ between latent variable $$$z$$$ and image $$$x$$$ parameterized with $$$\theta$$$. Here, the latent variable $$$z$$$ follows the simple probability distribution $$$p_Z$$$ (i.e., Gaussian distribution):$$z=f_\theta(x),{z}\sim{p_Z}\qquad(Eq. 1)$$Then the distribution of image can be formulated as:$$p_X(x)=p_Z(f_\theta(x))\left|det(\frac{\partial f_\theta(x)}{\partial x})\right|\qquad(Eq.2)$$Training can be conducted to minimize negative log-likelihood: $$$\mathcal{L}(\theta;x)=-log(p_X(x))=-log(p_Z(f_\theta(x))-log(\left|det(\frac{\partial f_\theta(x)}{\partial x})\right|)$$$. Image $$$x$$$ can be sampled by applying the inverse network: $$$x=f_\theta^{-1}(z),{z}\sim{p_Z}$$$.
[MRFlow] If the normalizing flow is trained only with the target domain, (Fig. 1; Step 1) the normalizing flow has learned a prior distribution of the target domain. The main idea for harmonization is to optimize the latent variable $$$z$$$ so that the optimized latent variable $$$\hat{z}$$$ is around the center of the Gaussian, and at the same time, the sampled image is not far from the image of the source domain. Because the normalizing flow has a prior of the target domain, the sampled image of the optimized latent variable $$$f_\theta^{-1}(z)$$$ would be the image harmonized from source to target. It can be formulated as an optimization equation:$${\hat{z}=\underset{z}{\mathrm{argmin}}\,\left|z\right|^2+\beta_1M\left|Gf_\theta^{-1}(z)\right|+\beta_2NCC(f_\theta^{-1}(z),x_s),}\\x_{harmonized}=f_\theta^{-1}(\hat{z}),\qquad(Eq. 3)$$where $$$\beta_1$$$ and $$$\beta_2$$$ are the regularization parameter, $$$x_s$$$ is the source domain image, $$$M$$$ is a mask where $$$x_s$$$ does not have any edges, $$$G$$$ is the gradient operator, and $$$NCC$$$ is normalized cross-correlation. The first term is to force the latent variable $$$z$$$ to be around the center of the Gaussian. The second term is for the edge coincidence of source and harmonized images, and the third term is for the similar trend of voxel values of source and harmonized images. The optimization of Eq. 3 is obviously not analytic, so we introduce an iterative method by taking advantage of the invertibility of the normalizing flow (Fig. 1; Step 2). $$\begin{align}&1.\;x_0=x_s,\;\alpha<<1\\&for\;n=0:N\;repeat\;2.\;and\;3.\\&2.\;z_n=(1-\alpha)f_\theta(x_n)\\&3.\;x_{n+1}=f(z_n)-\beta_1\triangledown_xM\left|Gx\right|_{x=f_\theta^{-1}(z_n)}-\beta_2\triangledown_xNCC(x,x_s)_{x=f_\theta^{-1}(z_n)}\end{align}$$
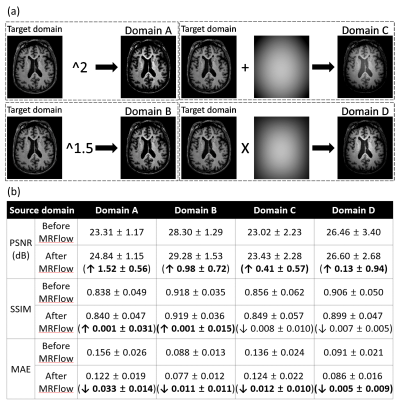
[Train and validation details] The SRFlow model⁶ was adopted as a network structure of the normalizing flow, with the substitution of the RRDB module to UNet. In order to improve the performance of the normalizing flow model, edge information of the input image was given as a condition, assuming the edge should be consistent across domains. The ADNI 2 dataset (3T image)⁹ was utilized as a target domain for the training normalizing flow. For a retrospective evaluation, source domain images were synthesized by manipulating the target domain image (e.g., gamma transformation and multiplication/summation with the low-frequency term; Fig. 2a). MRFlow was applied to the images of the generated source domain, and peak signal-to-noise ratio (PSNR), structural similarity (SSIM), and mean absolute error (MAE) were calculated. A prospective evaluation was also conducted using the ADNI 1 dataset (1.5T image) as a source domain. Histogram analysis was done for measuring the similarity between domains.

Results

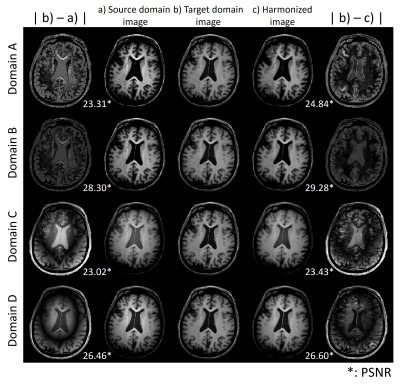
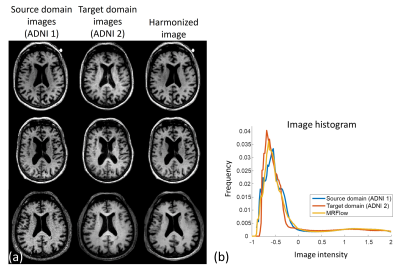
The results of retrospective experiments with synthesized source domains are illustrated in Figure 2b and Figure 3. For all synthesized source domains, the harmonized images using MRFlow showed lower overall errors than source domain images with the reference of target domain images (PSNR: 25.28 ± 3.13 dB → 26.04 ± 2.96 dB), but also demonstrated slightly decreased SSIM in some source domain cases. In Figure 4, the MRFlow harmonization results from the source domain (ADNI 1) to the target domain (ADNI 2) are displayed. The harmonized images show similar contrast and noise level to the target domain images, despite blurring and small artifacts. The histogram of harmonized images is closer to that of the target domain when compared to the source domain histogram (Fig 4b).

Conclusion and Discussion

In this study, we propose MRFlow, which is a preliminary study of the normalizing flow-based MR image harmonization method. Compared to other deep learning-based harmonization methods, our method has the advantage that it can be applied to the domain unseen during training. Still, MRFlow cannot be applied to a situation with large domain gaps, such as harmonization between multi-contrast, but this study demonstrates that harmonization is possible with a generative network trained only with the target domain, without requiring source domain information during training.

Acknowledgements

This work was supported by the BK21 FOUR program of the Education and Research Program for Future ICT Pioneers, Seoul National University and the Korea Agency for Infrastructure Technology Advancement(KAIA) grant funded by the Ministry of Land, Infrastructure and Transport (Grant 21NPSS-C163415-01)