0106
High Resolution Diffusion Tensor Imaging using Rapid Single-Slab 3D EPI Encoding
Hyunkyung Maeng1 and Jaeseok Park1,2
1Department of Biomedical Engineering, Sungkyunkwan University, Suwon, Korea, Republic of, 2Department of Intelligent Precision Healthcare Convergence, Sungkyunkwan University, Suwon, Korea, Republic of
1Department of Biomedical Engineering, Sungkyunkwan University, Suwon, Korea, Republic of, 2Department of Intelligent Precision Healthcare Convergence, Sungkyunkwan University, Suwon, Korea, Republic of
Synopsis
Keywords: Data Acquisition, Diffusion Tensor Imaging, High resolution 3D DTI
To propose an accelerated high resolution whole brain DTI and investigate its feasibility (1.0$$$mm^3$$$ isotropic spatial resolution, imaging time ~ 15 min)Introduction
Diffusion tensor imaging (DTI)1 is to provide information on anisotropic diffusivity and hence characterize microscopic architecture. Nevertheless, it is still challenging to achieve highly well-defined diffusion information in whole brain MRI due to limited spatial resolution and prolonged imaging time. Whole brain DTI with single-slab 3D imaging is promising method with high signal-to-noise ratio (SNR) and no slab boundary artifact, but recent studies have some limitations in terms of the low spatial resolution (>1 $$$mm^3$$$)2, insufficient whole brain coverage, and low magnetic field strength (<3T)3. To address these issues, we first propose accelerated diffusion weighted imaging using single-slab 3D segmented EPI with pseudo-linear random sampling in k-q space to be capable of reduced scan time. Second, we combine locally low rank constrained reconstruction to achieve artifact-free diffusion weighted images by exploiting spatial-angular redundancies. Finally, we investigated the feasibility of accelerated high resolution whole brain DTI on a 3T scanner (1.0$$$mm^3$$$ isotropic spatial resolution, imaging time ~ 15 min).Methods
High resolution single-slab 3D EPITo achieve our aim, a single-slab 3D segmented EPI with pseudo-linear random sampling in k-q space was developed. Fig 1 represents a schematic of the proposed single-slab 3D segmented EPI (diffusion weighted imaging and phase navigator to correct shot-to-shot variations) (Fig. 1a) and its corresponding incoherent encoding schemes in k-q space (Figs. 1b, c). Especially, we use a grouped, pseudo-linear undersampling strategy with some physical constraints which is employed to achieve incoherence and alleviate both amplitude and phase modulation which occur considerably along the 3D EPI readout simultaneously. With this grouping sampling schedule, the blip gradient amplitudes in the ky and kz directions are physically constrained to achieve smooth signal transition while avoiding abrupt gradient switching. Therefore, variable density incoherent undersampled k-space can be acquired without significant k-space modulation and is utilized for robust constrained reconstruction.
Spatial-angular low rank constrained reconstruction
Missing signals were interpolated by solving constrained optimization problem with spatial and angular, locally low rank priors exploiting the fact that the different diffusion contrasts share the brain structure in images. The formulation of the problem with additional sparsity prior is:
$$\mathcal{J} \left \{ \mathrm{\mathbf{X}=\left( \mathbf{x}_0,...,\mathbf{x}_{N_d-1}\right)} \right \} = \lambda_p\sum_{p=0}^{N_p-1}\left\|\mathcal{R}_p\left ( \mathbf{X} \right ) \right\|_{*} + \lambda_{\Psi}\sum_{d=0}^{N_d-1}\left\|\Psi\left ( \mathbf{x_d} \right ) \right\|_{1} \\s.t. \quad \mathbf{Y} = \mathbf{F_u}\mathbf{S}\mathbf{P}\mathbf{X}$$
where $$$\mathbf{Y}$$$ denotes the acquired k-space signal; $$$\mathbf{P}$$$ is the phase map for each shot and each diffusion direction; $$$\mathbf{S}$$$ is the sensitivity encoding operator; $$$\mathbf{F_u}$$$ is the Fourier transform operator with undersampling; $$$\mathbf{X}$$$ is the desired artifact-free DWI, which is $$$\mathbf{X} = \mathbf{vect}([\mathbf{x}_0,...,\mathbf{x}_{N_d-1}])$$$; $$$N_d$$$ is the number of diffusion encoding directions; $$$N_s$$$ is the number of shots in each DWI; $$$N_c$$$ is the number of coils. This problem is solved using variable splitting methods under the framework of alternating direction approach.
Experiments
Experimental studies were performed in 15 healthy volunteers on a 3T whole-body MR scanner (Prisma, Siemens Healthineers, Erlangen, Germany) using the proposed, rapid diffusion-weighted MR pulse sequence with a 52-channel head coil. The imaging parameters were: TE = 64ms, field-of-view (FOV) = 230×200×150 $$$mm^3$$$, matrix size = 220×192×144, readout bandwidth = 1140 Hz/Pixel, echo train length (ETL) = 32, and Flip Angle =90◦. Electrocardiogram synchronization was used to minimize periodic phase incoherence from cardiac motion. Six diffusion-directions with b=1000s/$$$mm^2$$$ were acquired for DTI study. In the prospective study, the reduction factor is 5.5 (total scan time: 15min). Additionally, the 2D single-shot EPI with 1×1×2mm resolution was acquired for comparison with the proposed method. Fractional anisotropy maps were generated using FSL4.
Results
Fig 2 shows the brain images reconstructed using a conventional SENSE (without priors) and proposed method in the absence (‘before PC’) and presence (‘after PC’) of inter-shot 3D phase correction. The images with different diffusion encoding directions were shown in different rows with SSIM. The proposed method with inter-shot 3D phase correction reveals higher SSIM with noise suppression. Fig 3 shows the repeated comparison with prospective undersampled data (R =5.5, total scan time ~ 15min). DWIs, FA maps, and colored FA maps are shown in different rows. White arrows indicate that the proposed method can delineate the fine structures in DTI without noise amplification. Finally, we report the comparison of whole brain DTI colored FA maps acquired using a conventional 2D single-shot EPI and the proposed method. The zoom-in images show the details of the brain structure, and the proposed method is superior in preserving fine details.Discussion and Conclusion
We successfully demonstrated that the accelerated, 3D diffusion tensor imaging can be produced over the whole brain roughly in 15 minutes without an apparent artifact and amplified noise. We need to further investigate It is expected that the proposed method widens the neurological and clinical utility of diffusion tensor imaging, although it needs to be further investigated.Acknowledgements
This work is supported in part by NRF-2018M3C7A1056887, KMDF-202011B35, and KMDF-202011C20.References
1. Basser PJ, Mattiello J, LeBihan D. MR diffusion tensor spectroscopy and imaging. Biophys J. 1994 Jan;66(1):259-67.
2. Zhang Q, Coolen BF, Nederveen AJ, Strijkers GJ. Three-dimensional diffusion imaging with spiral encoded navigators from stimulated echoes (3D-DISPENSE). Magn Reson Med. 2019 Feb;81(2):1052-1065.
3. Chang HC, Hui ES, C.P.L.X.C.N., 2018. Phase correction for three-dimensional (3d) diffusion-weighted interleaved epi using 3d multiplexed sensitivity encoding and reconstruction (3d-muser). Magn Reson Med 79, 2702–2712.
4. Jenkinson M, Beckmann CF, Behrens TEJ, Woolrich MW, Smith SM. FSL. Neuroimage 2012;62:782–790.
Figures
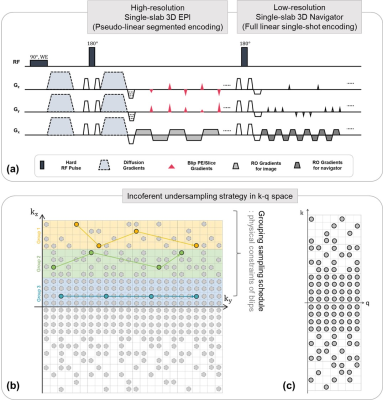
Figure 1. Fig 1a represents the sequence diagram of
the segmented 3D EPI with diffusion preparation. The diagram consists of the
imaging part for 3D diffusion MRI and the navigator part to correct the
shot-to-shot phase variation. Fig 1b-c represent examples of the pseudo-liner
random undersampling pattern in k-q space.
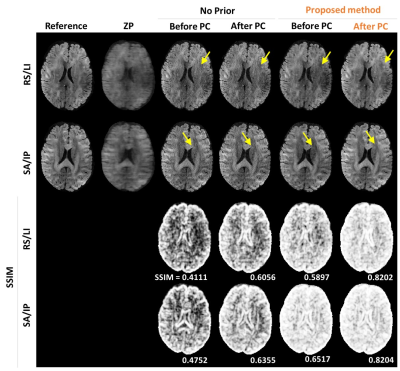
Figure 2. The reconstructed images and its
corresponding SSIM map between conventional SENSE and the proposed method at
reduction factor = 4. Note that the proposed method tends to suppress noise and
preserve structures.
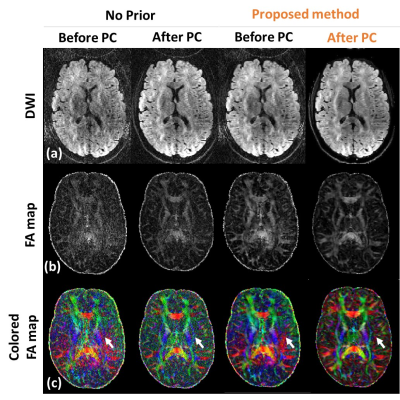
Figure 3. Fig 3 shows the repeated comparison with prospective
undersampled data (R =5.5, total scan time ~ 15min). DWIs (Fig 3a), FA maps
(Fig 3b), and colored FA maps (Fig 3c), are shown in different rows. White
arrows indicate that the proposed method can delineate the fine structures in
DTI without noise amplification.
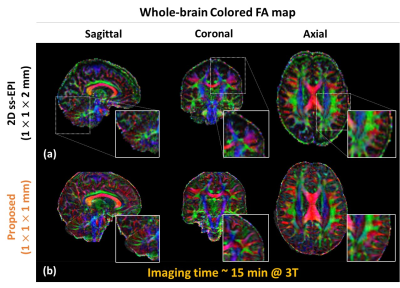
Figure 4. Sagittal, coronal, and axial slices of color-encoded FA maps
estimated from the (a) 2D single-shot EPI (b) proposed
method sets are shown. The superior performance in
delineating details becomes evident in this example. It is clear in regions including
cerebellum (zoomed-in images).
DOI: https://doi.org/10.58530/2023/0106