0074
A Novel Accelerated 3D Phase-Unwrapping Method Based on Subdivided Arrays and Polynomial Modeling with Application: Dixon Water-Fat Separation1Department of MRI, The First Affiliated Hospital of Zhengzhou University, Zhengzhou, China, 2College of Software Engineering, Zhengzhou University of Light Industry, Zhengzhou, China, 3Department of Radiation Oncology, Sun Yat-sen University CancerCenter, Guangzhou, China, 4School of Biomedical Engineering and Guangdong Provincial Key Laboratory of Medical Image Processing, Southern Medical University, Guangzhou, China
Synopsis
Keywords: Data Processing, Data Processing, phase imaging, phase unwrapping, Dixon technique
In this work, a novel robust and accelerated phase-unwrapping method is presented. The proposed method firstly introduces an artificial volume compartmentalization to break down the large-scale unwrapping problems, and then uses the phase partition method to cluster the phase into blocks to be paralleled unwrapped first, and residual-voxel to be unwrapped later. The simulated and in vivo datasets experiments have demonstrated that the proposed method allows for a reduction of the unwrapping problem size, a speed-up for handling large datasets, and obtains the accurate phase results under different SNRs and phase-change levels.
Target Audience
Researchers who are interested in fast 2D and 3D phase-unwrapping in Dixon water-fat separation and QSM techniques.Purpose
In MRI, to correctly calculate the phase values is important for many types of applications, such as quantifying blood-flow-velocity[1], characterizing chemical-shift effect[2], and temperature mapping[3]. Whereas the phase calculated from complex MR signals is generally wrapped into (-π, π] range, and is ambiguous. The wrapped phase should be correctly unwrapped to recover underlying true phase before applications. A large number of phase-unwrapping algorithms have been proposed, while most of them are generally challenged by noise and rapid-phase-change[4]. In addition, the computational efficiency of the phase-unwrapping method is vital for high-resolution imaging at ultra-high field, such as water-fat separation[5], SWI[6] and QSM[7].In this work, we propose a novel robust and accelerated 3D phase-unwrapping method that does not need to eliminate the region with low SNRs or/and rapid-phase-change[8]. Proposed method firstly subdivided wrapped phase into a number of rectangular arrays. The arrays were clustered into the blocks to be paralleled unwrapped first, and residual-voxel to be unwrapped later by phase partition method. The blocks were firstly processed and matched together. After that, the residual-voxel were unwrapped by exploiting the phase information of matched blocks. The 3D simulation and in vivo head-neck, breast and knee datasets were implemented to evaluate the performance of proposed method with comparisons to the Region_growing[9], Graph_cut[10] and SEGUE[11].
Methods
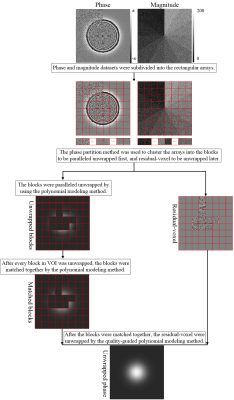
The 2D flowchart of proposed method is presented in Figure 1. The proposed method firstly subdivided the phase into rectangular arrays in the three orthogonal directions. The sizes of the arrays in every direction were added one to share the information of the edge voxels of each array. After that, every array was segmented into subarrays by phase partition method. The arrays were clustered into the blocks to be paralleled unwrapped first, and residual-voxel to be unwrapped later by thresholding the voxels number of the largest subarray in every array. The blocks were processed and matched together by using a polynomial modeling method[5]. After all block were matched together, the residual-voxel was unwrapped by using the quality-guided polynomial modeling method. The second difference of the phase was used as quality map[12].One simulated 3D Gaussian phase cube (256×256×100) was generated:$$\phi _{(x,y,z)} =25\times(1+0.1\times z)\times e^{\frac{-x^{2}-y^{2} }{2} } ,$$the standard deviations (SD) were 40 voxels. The magnitude increased from 10 to 120 with an increasement of 10 in x0y plane. Gaussian noises with SD of 20 rad were independently added to the real and imaginary parts of generated data. The misclassification ratio[13] was calculated as the incorrect unwrapped voxel ratio in VOI. The simulation was repeated 30 times, and the corresponding means and SDs of error ration (%) and running time (s) were separately calculated. The in vivo head-neck, breast and knee datasets were acquired on a 3.0T MRI scanner (Philips; Netherlands) from 6 volunteers using dual-echo FFE sequence (voxel-size=1.125×1.125×5mm3, TE1/TE2=1.2/2.3ms, TR=354ms). The program was implemented in Matlab on a desktop computer (Windows, 32 GB, Inter i7-8700). The arrays number in the simulated and in vivo experiments was all 8×8×4 in the three orthogonal directions.
Results
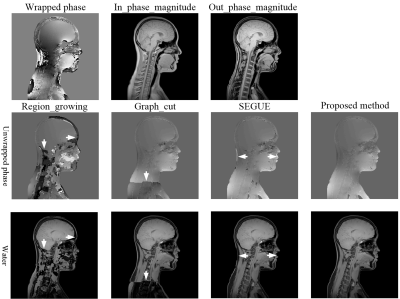
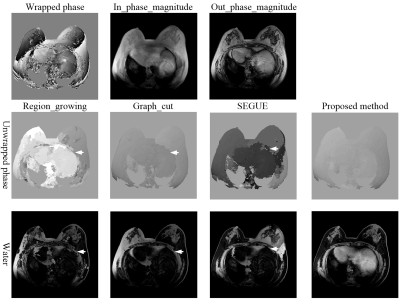
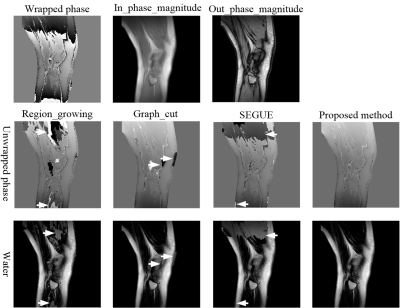
Figure 2 shows the phase-unwrapping results by Region_growing, Graph_cut, SEGUE and proposed method under different SNRs along clockwise direction in x0y plane, and different phase-variation levels along z axle direction. There are obvious wraps in the results by Region_growing, Graph_cut, and SEGUE, while proposed method obtains a smooth unwrapped phase. The mean and SD of error rates by Region_growing, Graph_cut and SEGUE are separately 42.32±18.67%, 4.28±0.19%, and 13.46±0.75%, which are all larger than that of proposed method. The mean and SD of error rates by proposed method is 0.14±0.08%. The mean and SD of running times by Region_growing, Graph_cut, SEGUE and proposed method are separately 4.5±0.2s, 43624.0±1038.7s, 7957.1±512.5s and 1137.2±113.8s. Region_growing and proposed methods are faster than Graph_cut and SEGUE algorithms. Graph_cut and Region_growing methods were programed by C, while SEGUE and proposed methods were programed by Matlab. After running more than 24 hours, the unwrapped phase by the PRELUDE method[13] has not been generated.Figures 3-5 show the representative phase-unwrapping and water-fat separation results of in vivo head-neck, breast and knee datasets by Region_growing, Graph_cut, SEGUE and proposed algorithms, respectively. The results of Region_growing, Graph_cut and SEGUE still contain obvious phase discontinuities and water-fat swaps where the arrows point to, while proposed method shows the results with no obvious errors residues.
Discussions and Conclusions
In this work, a novel robust and accelerated phase-unwrapping method is presented. Proposed method firstly introduces an artificial volume compartmentalization to break down the large-scale unwrapping problems, and then uses phase partition method to cluster the phase into blocks to be paralleled unwrapped first, and residual-voxel to be unwrapped later. This strategy can guarantee proposed method does not need a refined mask to remove the voxels with low SNRs or/and rapid-change-phase in VOI, and unwrap the voxels with high SNR or/and slow-change-phase in parallel to accelerate. The simulated and in vivo datasets experiments have demonstrated that the proposed method allows for a reduction of the phase-unwrapping problem size, a speed-up for handling large datasets, and obtains the accurate phase results under different SNRs and phase-change levels.Acknowledgements
This work was supported by the Union Project of Medical and Technology Research Program of Henan Province (LHGJ20190159), and the Science and Technology Planning Program of Henan Province (Grant Nos. 212102310088, 212102310886 and 2020GGJS123)References
[1] Dumoulin CL, Souza SP, Walker MF, Wagle W. Three-dimensional phase contrast angiography. Magn Reson Med. 1989; 9:139-149.
[2] Ma J. Dixon techniques for water and fat imaging. J Magn Reson Imaging 2008; 28(3): 543-558.
[3] Ishihara Y, Calderon A, Watanabe H, et al. A precise and fast temperature mapping using water proton chemical shift. Magn Reson Med. 1995; 34:814-823.
[4] Ghiglia DC, Pritt MD. Two-Dimensional Phase Unwrapping: Theory, Algorithms, and Software. New York: Wiley; 1998.
[5] Cheng J, Mei Y, Liu B, et al. A novel phase-unwrapping method based on pixel clustering and local surface fitting with application to Dixon water–fat MRI. Magn Reson Med 2018 Jan; 79(1):515-528.
[6] Rauscher A, Sedlacik J, Barth M, et al. Magnetic susceptibility-weighted MR phase imaging of the human brain. American Journal of Neuroradiology 2005; 26(4): 736-742.
[7] Haacke EM, Liu S, Buch S, et al. Quantitative susceptibility mapping: current status and future directions. Magn Reson Imaging 2015; 33(1): 1-25.
[8] Lindemeyer J, Oros-Peusquens AM, Shah NJ. Quality-based UnwRap of SUbdivided Large Arrays (URSULA) for high-resolution MRI data. Med Image Anal 2019 Feb; 52:13-23.
[9] Schofield M A, Zhu Y. Fast phase unwrapping algorithm for interferometric applications. Optics letters 2003; 28(14): 1194-1196.
[10] Dong J, Chen F, Zhou D, et al. Phase unwrapping with graph cuts optimization and dual decomposition acceleration for 3D high‐resolution MRI data. Magn Reson Med 2017; 77(3): 1353-1358.
[11] Karsa A, Shmueli K. SEGUE: A Speedy rEgion-Growing Algorithm for Unwrapping Estimated Phase. IEEE Transactions on Medical Imaging 2019; 38(6):1347-1357.
[12] Hussein S. Abdul-Rahman, Munther A. Gdeisat, et al, Fast and robust three-dimensional best path phase unwrapping algorithm, Appl. Opt. 2007; 46, 6623-6635.
[13] Jenkinson M. Fast, automated, N-dimensional phase-unwrapping algorithm. Magn Reson Med 2003; 49:193–197.
Figures