Semiclassical Theory of Relaxation
Valerij G. Kiselev1
1University Medical Center Freiburg, Germany
1University Medical Center Freiburg, Germany
Synopsis
The goal of this lecture is to explain the mechanisms of relaxation caused by the thermal motion of molecules. The focus is on emergence and the role of the correlation functions of random magnetic field. Properties of these functions help understanding the dependence of longitudinal and transverse relaxations on the rate of molecular motion. The difference in these dependencies is the key for explaining several phenomena practically important for NMR and MRI. This lecture relies on the basic notions of analysis, quantum mechanics, statistical physics and Fourier transformation.
On Relaxation
Why don't we use quantum mechanics in our daily MRI work? The reason is a huge number of spins in any MRI voxel. While quantum mechanics gives only statistical predictions, averaging over such a large number restricts the outcome to the expectation values with negligible fluctuations around them. There are of course pulse sequences specially designed for measuring quantum effect. We do not consider them now focusing on the basic phenomenon of precession and relaxation of spins 1/2.The expectation value of spin can parametrize an arbitrary spin state. The expectation value is a vector with the components equal the quantum mean of the three operators of spin projections, $$$\langle S_x \rangle = \psi^\dagger S_x \psi$$$, and the analogous $$$\langle S_y \rangle$$$ and $$$\langle S_z \rangle$$$ (Fig.1). This parametrization helps to instantly see the magnetization of a large number of spins prepared in the same quantum state. In particular, the solution to the Schrödinger equation immediately demonstrates the spin precession in an applied $$$B_z$$$ field expressed as the conjugated phases acquired by the top and down spinor components. The spin excitation, which is precession around a rotating axis in the $$$x-y$$$ plane, is seen as the relative magnitudes of the spinor components.
In contrast to such coherent spin manipulations, any random component of magnetic fields results in relaxation. It is straightforward to analyze a simplified situation with the only random field $$$B_z$$$. Since the precession phase accumulates the instantaneous precession frequency, different spins acquire different phases when exposed to independent random fields $$$B_z$$$. This results in a decrease in the vector sum of the transverse magnetizations, which is the measurable signal. This decrease is called the transverse relaxation. Emergence of the field correlation function is explained in the lecture. In more detail, the relaxation rate is proportional to the Fourier transform of this function taken at the frequency $$$\omega=0$$$ (which is simply the time integral).
The longitudinal relaxation differs in two respects. First, the applied fields $$$B_x$$$ and $$$B_y$$$ affect the spin being effectively multiplied with the factors $$$e^{\pm i\Omega_0 t}$$$, where $$$\Omega_0$$$ is the Larmor frequency. It follows from the Schrödinger equation and results in the emergence of the field correlation function represented via its Fourier transform taken at the frequency $$$\omega=\Omega_0$$$. Second, the described semiclassical theory of relaxation results in a dispersion in the longitudinal magnetization, which causes the attenuation towards zero rather than the equilibrium magnetization. This follows from the framework of this theory in which spins are described quantum-mechanically while their environment is represented by the classical random fields.
One can guess that the dispersion of longitudinal magnetization can be biased towards a non-zero equilibrium when a corresponding driving force is applied. Such an effective force is taken into account in the quantum theory of relaxation that considers the spin's environment using quantum statistical physics. In brief, a change in the spin longitudinal magnetization (a spin flip) occurs with a corresponding energy-conserving transition in the environment. The environment is however a thermal bath that slow dissipates its energy to stay at the Bolzmann distribution. This distribution is thus transferred to the spin system.
On Mechanisms
The physical origin of the random magnetic field is always the molecular motion, in particular, the random rotations. Considering a water molecule with two protons, the dipole-dipole interaction of these protons depends on the protons orientation relative to the main field. Random orientations result in random interaction energy considered above within the semiclassical relaxation theory. Rotation of water molecules in liquid state is very fast with a correlation time $$$\tau \sim 1\,\rm ps$$$.The dependence of transverse and longitudinal magnetization on the field correlation function taken at zero and Larmor frequency, respectively results in distinct dependencies on the field correlation time In other words, it is the dependence on the rate of molecular motion also called the tumbling rate, Fig.2. This plot helps understanding the relaxation behavior, in particular, of protons. The correlation time of molecular motion in liquid water is very short as compared with the Larmor frequency, $$$\Omega_0\tau \ll 1$$$. This explains the equal transverse and longitudinal relaxation rates in pure water. However, large molecules move slowly. That is why protons in lipids experience random magnetic field with a longer correlation time. This explains a faster relaxation in fat tissue, the fact commonly used for the fat suppression with the inversion recovery. Also, water molecules can temporarily bind to a large, slowly moving macromolecule. In this case, the correlation time gets much longer bringing the relaxation in the regime with two essentially different relaxation rates.
This difference defines in particular the different spatial extents of the effect of contrast agents. Since the longitudinal relaxation rate peaks at $$$\tau \sim \Omega_0$$$, the effect is local: Contrast agent affects only water molecules in a narrow vicinity. Considered on the scale of tissue microstructure, the effect is limited to the volume actually doped with the contrast agent. It is not so for transverse relaxation: The effect of contrast agent can span outside its actual location as it is in the case of fMRI based on the BOLD effect. Physics of relaxation in tissues is beyond the scope of this lecture. The discussed property of transverse relaxation is a road sign pointing on the link to transverse relaxation on the tissue scale, which deserves a dedicated consideration.
Acknowledgements
No acknowledgement found.References
Maurice Goldman. Quantum description of high-resolution NMR in liquids. Oxford University Press, 2000. Valerij G Kiselev and Dmitry S Novikov. Transverse NMR relaxation in biological tissues. NeuroImage, 182 (2018) 149--168.Figures
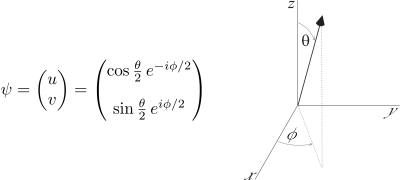
A generic spinor with two complex-valued components is subjected to two constraints: (i) The normalization on the probability of any state to be unity and (ii) the irrelevance of the overall phase. This leaves only two independent real parameters, which can be selected as the angles defining the direction of the spin expectation value in the polar coordinate system. This expectation vector is the contribution of a given spin to the classical sum in a large sample.
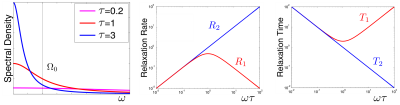
Left: The profile of the Fourier-transformed field correlation function for variable correlation time. The variance of the field remains fixes (e.g. when treating the two water protons always separated by the same distance). In the Fourier domain, this implies a fixed area under the plot, while longer correlation time is seen as the peak narrowing. This leads to distinct behavior of transverse (the value at zero frequency) and longitudinal relaxation rates (the value at the Larmor frequency, middle image).