5046
Concomitant Field Effects on Asymmetric Gradient Systems: Impacts on Slow Flow Imaging1GE Global Research Center, Niskayuna, NY, United States, 2Walter Reed National Military Medical Center, Bethesda, MD, United States, 3Uniformed Services University of the Health Sciences, Bethesda, MD, United States, 4Department of Radiology, Mayo Clinic, Rochester, MN, United States
Synopsis
This study investigates concomitant gradient field effects on gradient echo phase contrast imaging when visualizing very slow (<50 mm/s) flow. The impact of real-time concomitant field compensation and the consequence of uncompensated higher-ordered terms is shown.
Introduction
High-performance head gradient subsystems1–5 are capable of producing gradient fields up to 400mT/m. These asymmetric gradients report higher efficiency and peripheral nerve stimulation thresholds compared to whole-body MRI systems6. However, high-gradient amplitudes and asymmetric coil design introduce zeroth- and first-order7,8 concomitant gradient fields (CF), in addition to the higher order-field terms encountered with symmetric gradient designs. CF effects manifest as non-linear spatially-varying contributions resulting in errors due to phase accumulation, echo shifting, geometric distortion (in EPI), incorrect diffusion b-values, and errant phase-velocity measurements (phase-contrast (PC) imaging)9.Flow quantification based on the velocity-dependent phase evolution of flowing spins, consists of two successive measurements with identical zeroth moments but differing first moments8,10. For bipolar flow encoding, the net phase exhibits zero phase due to flow, and a non-zero component due to residual eddy current and CF effects11. At velocity encoding (VENC) values of >50 mm/s, the uncompensated (2nd order) CF effects are not significant. However, in probing slow flow in the brain (interstitial, cerebrospinal and glymphatic flow13–16) with VENC=0.1-5 mm/s second order effects degrade the gradient echo signal rendering it impossible to utilize gradient echo PC.
As such, to understand the root cause for image artifacts at ultra-low VENC values (Fig.1), we investigated the effect of CF of zeroth, first, second, and higher-order with a bipolar flow-encoding acquisition. The objective is to 1) demonstrate the impact of real-time compensation, and the footprint of uncompensated terms, and 2) to predict the magnitude of the field needed for compensation.
Methods
The basis for CFs has been defined in detail7,8,17. To highlight the effect CFs are expressed as,$$\mid B(x,y,z)\mid\doteq B_{0}\dotplus G_{x}x\dotplus G_{y}y\dotplus G_{z}z\nonumber\\+(\frac{G_x^2z_{0x}^2}{2B_0}+\frac{\alpha^2G_z^2x_0^2}{2B_0}-\frac{\alpha G_xG_zz_{0x}x_0}{B_0}+\frac{G_y^2 z_{0y}^2}{2B_0}+\frac{(1-\alpha)^2G_z^2y_0^2}{2B_0}-\frac{(1-\alpha)G_yG_zz_{0y}y_0}{B_0})\nonumber\\+\frac{G_x^2zz_{0x}}{B_0}+\frac{\alpha^2G_z^2xx_{0}}{B_0}-\frac{\alpha G_xG_zxz_{0x}}{B_0}-\frac{\alpha G_xG_zzx_{0}}{B_0}+\frac{G_y^2zz_{0y}}{B_0}+\frac{(1-\alpha)^2G_z^2yy_{0}}{B_0}-\frac{(1-\alpha)G_yG_zyz_{0y}}{B_0}-\frac{(1-\alpha)G_yG_zzy_{0}}{B_0}\nonumber \\+\frac{\alpha^2G_z^2}{2B_0}x^2+\frac{(1-\alpha)^2G_z^2}{2B_0}y^2+\frac{(G_x^2+G_y^2)}{2B_0}z^2-\frac{\alpha G_xG_z}{B_0}xz-\frac{(1-\alpha)G_yG_z}{B_0}yz\nonumber\\-\frac{z^3}{2B_0^3}(G_x^4z_{0x}+G_y^4z_{0y}+G_x^2G_y^2z_{0x}+G_x^2G_y^2z_{0y})+...$$
Zeroth and first order CF effects can be corrected in real-time11,12. However, even-ordered CF terms, common to both symmetric and asymmetric coils are difficult to correct in real-time. Higher odd-ordered (≥3rd) terms exert a negligible effect even for Gmax=200 mT/m. The maximum CF from the zeroth, first, and second order terms is <210 $$$\mu$$$T, whereas the maximal third order CF error ≤0.05 $$$\mu$$$T (spatial contribution order $$$\frac{G^{4}z^{3}z_{0_{x,y}}}{B_0^3}$$$). The contribution of the 2nd order CF term is ~110 $$$\mu$$$T (i.e., ~0.5 total CF).
All phantom experiments were conducted in a whole body 3.0T fitted with a asymmetric head-only high-performance gradient coil (MAGNUS) producing Gmax=200 mT/m and SRmax=500 T/m/s (1 MVA). A conventional PC pulse sequence with balanced bipolar flow-encoding8 was utilized. A 17-cm diameter silicone oil/gel sphere phantom was used and allowed to settle overnight. PC scans were performed to capture spatially varying phase in z- with imaging parameters: Sagittal plane, FOV=24-cm, acquisition matrix=256x256, ±15.6 kHz receiver bandwidth, slice thickness=10 mm, flow encoding=A/P&R/L separately, VENC=100, 50, 10, 5, and 1 mm/s, TR=30 ms, and flip angle=15˚. Experiments were performed with, 1) no CF compensation 2) zeroth order compensation only, 3) first order compensation only, 4) zeroth and first order compensation, and 5) derated gradients (50%Gmax).
Results and Discussion
Simulations12 underscore that without CF corrections for VENC=1 mm/s considerable phase errors were observed (~20 radians/cm)(Fig.2). The phase errors are spatially dependent and lead to echo shifting (outside the acquisition window) and k-space dispersion(Fig.3). Subsequently, these errors lead to image degradation and signal dropout without any compensation(Fig.4). This result renders taking the phase difference impossible as the individual flow encoding source images are severely degraded(Fig.4-5)Echo shift and phase dispersion was observed to be different for flow encoding AP versus RL(Fig.3). The observed echo shift and phase dispersion was somewhat mitigated by compensating for first order CF in real-time. However, significant k-space spread of the echo remained and is due primarily to uncompensated 2nd order CF terms(Eqn.(1)) which has a quadratic spatial dependence in x, y, and z (depending on the flow encoding direction).
Phase maps illustrate spatially dependent phase without any CF compensation (Fig.5,red-arrows), with line plots highlighting the correction of zeroth order (constant phase offset) and first order (linear phase in z) CF effects. What remains is a z2 phase due to 2nd order CF effects that are normally corrected after phase difference processing8. However, the post-correction is possible only if the echo has not shifted outside the acquisition window.
Second order field effects cannot be readily compensated in real-time, but compensation must be performed to allow VENC<5 mm/s for gradient echo PC. For real-time correction, a z2 shim coil can be integrated as long as the coil current can be dynamically controlled with a 4 ms temporal resolution. For a whole body (60-cm bore) z2 higher order shim (HOS) coil, a 15A power supply yields a max current field of ~34Hz/cm2. The residual field from 2nd order effects was estimated <24Hz/cm2 indicating that a standard HOS z2 coil has sufficient field to compensate for 2nd order concomitant effects. We note that the echo shifting and phase dispersion for 2nd order CF effects are substantially reduced with spin echo acquisitions, permitting PC acquisitions down to VENC=0.2 mm/s14
Conclusion
Second order cross- and self-squared terms are not specific to asymmetric gradient coils. As such, echo shift and phase dispersal will also be observed in symmetric and whole-body systems with high Gmax. Dedicated second-order corrections are needed specifically for ultra-low VENC gradient-echo PC.Acknowledgements
Grant funding from NIH U01EB028976, NIH U01EB024450, CDMRP W81XWH-16-2-0054References
1. Foo, T. K. F. et al. Magn Reson Med 83, 2356–2369 (2020).
2. Foo, T. K. F. et al. Magn Reson Med 80, 2232–2245 (2018).
3. Weiger, M. et al. Magn Reson Med 79, 3256–3266 (2018).
4. Feinberg, D. A. et al. Proceedings of the 29th Annual Meeting of the ISMRM, Virtual Meeting (2021)
5. Setsompop, K. et al. NeuroImage 80, 220–233 (2013).
6. Tan, E. T. et al. Magn Reson Med 83, 352–366 (2020).
7. Meier, C., et al. Magnetic Resonance in Medicine 60, 128–134 (2008).
8. Bernstein, M. A. et al. Magn Reson Med 39, 300–308 (1998).
9. Weavers, P. T. et al. Magn Reson Med 79, 1538–1544 (2018).
10. Pelc, N. J., et al. Journal of Magnetic Resonance Imaging 1, 405–413 (1991).
11. Foo, T. et al. Proceedings of the 29th Annual Meeting of the ISMRM, Virtual Meeting (2021)
12. Tao, S. et al. Magn Reson Med 77, 2250–2262 (2017).
13. Williamson, et al. Journal of Magnetic Resonance Open 2–3, 100004 (2020).
14. Jansen, I. H. et al. Proceedings of the 28th Annual Meeting of the ISMRM, Virtual Meeting (2020)
15. Shih, Robert Y. et al. Proceedings of the 28th Annual Meeting of the ISMRM, Virtual Meeting (2020)
16. Yildiz, S. et al. Magn. Reson. Imaging 46, 431–439 (2017).
17. King, K. F., et al. Magn Reson Med 41, 103–112 (1999).
18. Tao, S. et al. Magn Reson Med 77, 2250–2262 (2017).Figures
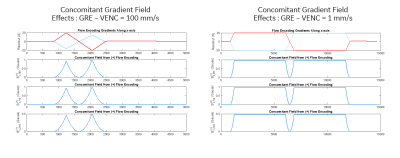

Figure 2. Comparison of the uncompensated (A) and theoretically compensated (B) waveforms for venc = 1 mm/s and associated phase accrual. A substantial offset is observed without compensation over the lobes of the flow encoding gradients and is parabolic in the z-direction. DC and Linear offset compensation mitigate the impacts but retaining the parabolic profile.

Figure 3. k-space echo with and without real time compensation for zeroth and first order CF is demonstrated with the horizontal axis highlighting ky. Switching the flow encoding directions highlights the differential z2 impact from concomitant fields impacting both the phase and flow encoding directions. Line plots through isocenter demonstrate the same phenomena, where without compensation echo spread and shift is noted.
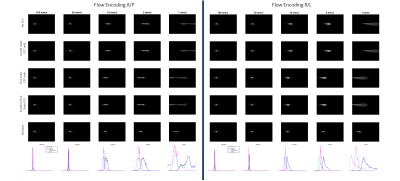
Figure 4. Magnitude phase contrast images across a 17-cm diameter silicone oil phantom for data sampled over a sagittal slice. Without compensation (top row) as the gradient amplitude for flow encoding is increased, signal dropout is evident.
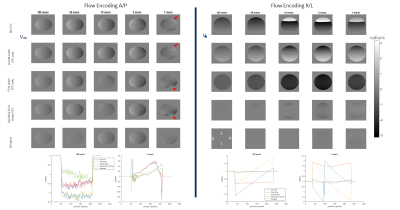
Figure 5. Phase maps reconstructed from phase difference data demonstrate phase from uncompensated and residual phase from real-time compensated acquisitions. Line plots in SI are shown. Substantial loss in coherent phase (red arrow) was noted without any compensation. Real-time zeroth order compensation accounts the constant phase offset, first order compensation accounts for the linear phase variation. The residual quadratic phase is attributed to second-order terms with mitigation observed by derating the gradients to 50% Gmax.