5022
Automatic Off-Resonance Correction for Spiral Imaging with a Convolutional Neural Network
Quan Dou1, Zhixing Wang1, Xue Feng1, and Craig H. Meyer1
1Biomedical Engineering, University of Virginia, Charlottesville, VA, United States
1Biomedical Engineering, University of Virginia, Charlottesville, VA, United States
Synopsis
Off-resonance is a major limitation for spiral imaging. A convolutional neural network was implemented in this study to correct off-resonance artifacts without field maps. The network was trained on images with simulated blurring artifacts. The image quality was improved after the correction for both simulated data and in vivo data.
Introduction
Spiral data sampling has several advantages, such as short echo time, high scan efficiency, and motion robustness. However, spiral imaging is limited by blurring artifacts raised from off-resonance effects, especially with long readouts. Most existing deblurring methods require prior knowledge about the field map1-4. Automatic off-resonance correction methods do not require field maps, but their performance is highly dependent on the choice of the objective function and frequency searching range5,6. Recently, convolutional neural networks (CNNs) demonstrated promising results for image deblurring7,8. In this work, we aimed to develop a CNN to perform automatic off-resonance correction for spiral imaging.Methods
An open-source data set9 (https://fastmri.med.nyu.edu/) containing Cartesian T2-weighted images for 4179 subjects was used. Single-coil data was simulated from the multi-coil data using an emulated single-coil method10. We randomly selected 1000 subjects and divided the 1000 imaging volumes such that 750 volumes were used for training and validation, and the remaining 250 volumes were used for testing.To generate paired training data with spiral off-resonance artifacts, a field map was first simulated by combining a random 2D polynomial with several random 2D Gaussian functions. A brain mask was applied to the generated field map to simulate the abrupt off-resonance change at the air-tissue boundary. The frequency range of the simulated field map was limited to between [-500 Hz, +500 Hz]. Then, a spiral k-space trajectory was simulated based on the image field of view (FOV) and resolution, and the corresponding Cartesian k-space time map was calculated for faster computation. The number of spiral interleaves was randomly selected between [4, 64], and the readout length for one interleave was between [4 ms, 24 ms]. The synthesized blurred image was obtained by applying the simulated field map to the ground truth through multifrequency interpolation (MFI)2, as shown in Figure 1.
To correct the off-resonance artifacts, we developed and trained a CNN with 3 residual blocks11 that we termed AutofocusNet. The blurred image was first demodulated at 11 different frequencies, which is also the first step in the conventional autofocus method5. The input of the network was a series of the 11 images, with 22 channels corresponding to real and imaginary components. The output was the deblurred image, with 2 channels corresponding to real and imaginary components. Each residual block consists of two 5 × 5 convolutional layers with filter depths of 128, followed by rectified linear unit (ReLU) activations. A skip connection was added between the block input and output, as shown in Figure 2. The network was implemented in PyTorch12. L1 loss between the network output and ground truth was optimized using Adam13 with a learning rate of 0.0001. To avoid overfitting, we adopted random patch cropping as the training augmentation. The structural similarity index (SSIM) and peak signal-to-noise ratio (PSNR) were calculated as image quality metrics to evaluate the network performance on the simulated dataset. The trained network was also applied to a phantom image and a head image of a healthy volunteer acquired on a Siemens Avanto 1.5T scanner. The spiral imaging parameters were FOV = 28 cm2, matrix size = 512 × 512, number of interleaves = 14, and readout length = 16.4 ms. Semiautomatic correction14 utilizing a low-resolution field map was also performed for comparison.
Results
Figure 3 shows the network performance on an image with simulated spiral off-resonance artifacts. Compared to the blurred image, the network output showed less artifacts, sharper structures, and higher image quality. Quantitatively, the average SSIM and PSNR of the simulated dataset were increased from 0.7231 and 26.84 to 0.9365 and 36.71 after off-resonance correction. The network performance on a phantom image and a in vivo head image collected with spiral scans were shown in Figure 3 and Figure 4, respectively. The network effectively recovered the image sharpness and improved the image quality in both cases. These results showed that the network could correct off-resonance artifacts for images outside the training dataset population.Discussion
In this study, we implemented a CNN to correct spiral off-resonance artifacts without field maps. To train the network, we synthetically generated blurred images with simulated field maps. We tested the network performance with simulated data and in vivo data which was outside the training dataset distribution. The network removed blurring in both situations with an average processing time of 50 ms for a single slice on a single GPU (not including the I/O time). We believe that our network can be generalized for concomitant gradient correction.Acknowledgements
This work was supported in part by Siemens Healthcare.References
[1] Noll DC, Meyer CH, Pauly JM, Nishimura DG, Macovski A. A homogeneity correction method for magnetic resonance imaging with time-varying gradients. IEEE Trans Med Imaging. 1991;10(4):629-37.[2] Man LC, Pauly JM, Macovski A. Multifrequency interpolation for fast off-resonance correction. Magn Reson Med. 1997 May;37(5):785-92.
[3] Ahunbay E, Pipe JG. Rapid method for deblurring spiral MR images. Magn Reson Med. 2000 Sep;44(3):491-4.
[4] Sutton BP, Noll DC, Fessler JA. Fast, iterative image reconstruction for MRI in the presence of field inhomogeneities. IEEE Trans Med Imaging. 2003 Feb;22(2):178-88.
[5] Noll DC, Pauly JM, Meyer CH, Nishimura DG, Macovski A. Deblurring for non-2D Fourier transform magnetic resonance imaging. Magn Reson Med. 1992 Jun;25(2):319-33.
[6] Man LC, Pauly JM, Macovski A. Improved automatic off-resonance correction without a field map in spiral imaging. Magn Reson Med. 1997 Jun;37(6):906-13.
[7] Zeng DY, Shaikh J, Holmes S, Brunsing RL, Pauly JM, Nishimura DG, Vasanawala SS, Cheng JY. Deep residual network for off-resonance artifact correction with application to pediatric body MRA with 3D cones. Magn Reson Med. 2019 Oct;82(4):1398-1411.
[8] Lim Y, Bliesener Y, Narayanan S, Nayak KS. Deblurring for spiral real-time MRI using convolutional neural networks. Magn Reson Med. 2020 Dec;84(6):3438-3452.
[9] Zbontar J, Knoll F, Sriram A, et al. fastMRI: An Open Dataset and Benchmarks for Accelerated MRI. 2018. arXiv:1811.08839 [cs.CV].
[10] Zbontar J, Tygert M. Simulating single-coil MRI from the responses of multiple coils. 2018. arXiv:1811.08026 [eess.IV].
[11] He K, Zhang X, Ren S, Sun J. Deep residual learning for image recognition. 2015. arXiv:1512.03385 [cs.CV].
[12] Paszke A, Gross S, Massa F, et al. PyTorch: An Imperative Style, High-Performance Deep Learning Library. 2019. arXiv:1912.01703 [cs.LG].
[13] Kingma DP, Ba J. Adam: A Method for Stochastic Optimization. 2014. arXiv:1412.6980 [cs.LG].
[14] Chen W, Meyer CH. Semiautomatic off-resonance correction in spiral imaging. Magn Reson Med. 2008 May;59(5):1212-9.
Figures
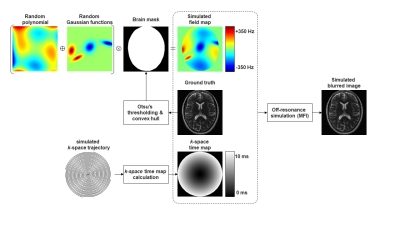
Figure 1. Generation of training data.
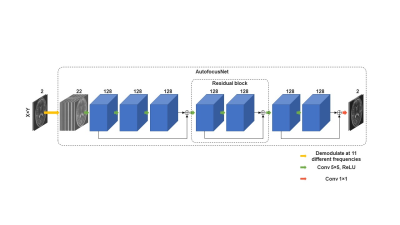
Figure 2. Proposed CNN architecture.
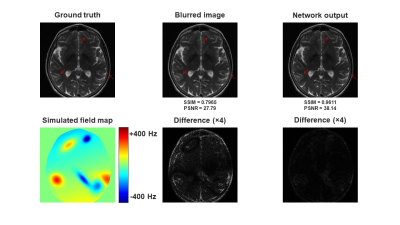
Figure 3. Representative off-resonance correction results on simulated data.

Figure 4. Off-resonance correction results on a phantom image acquired using a spiral scan.
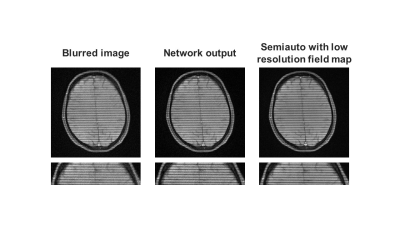
Figure 5. Off-resonance correction results on a head image of a healthy volunteer acquired using a spiral scan with SPAMM tagging to aid visualization of blurring.
DOI: https://doi.org/10.58530/2022/5022