5012
Learned 3D radial trajectories using Image Quality Metrics from Prior Data1Medical Physics, University of Wisconsin-Madison, Madison, WI, United States, 2Radiology, University of Wisconsin-Madison, Madison, WI, United States, 3University of Wisconsin-Madison, Madison, WI, United States
Synopsis
3D radial sampling provides high levels of acceleration with insensitivity to motion. Methods of designing the radial projection angles and orders have been focused on improving the sampling uniformity, which is indirectly related to image quality. We propose a flexible framework to optimize the sampling directly based on image reconstruction metrics. We demonstrated the optimized trajectories were able to produce higher quality images in both simulations and scans.
Introduction
Three-dimensional radial trajectories have been successfully implemented for motion robust flow, pulmonary, cardiac, and dynamic contrast enhanced imaging by virtue of oversampling the center of k-space and efficient coverage . However, the design of optimal projection distributions and ordering remains a challenge. A variety of approaches have been proposed to achieve the best uniformity in the sampling, such as placing the projection endpoints on a spherical spiral [1], spherically mapped 2D golden means [2], spiral phyllotaxis [3], and minimizing the transfer function of the sampling coordinates [4]. One challenge of these methods is that better sampling uniformity might not necessarily translate to higher image quality for specific anatomies and applications. In this work, we propose to optimize the sampling coordinates by exploiting image quality metrics from prior data and reconstruct images resampled from existing training datasets with these coordinates.Methods
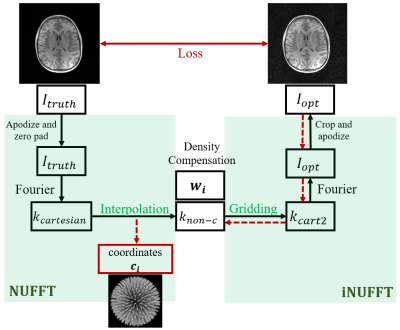
Our method is illustrated in Figure 1, based on a bank of ground truth images. Cartesian k-space data $$$k_{cartesian}$$$ retrieved from the truth images $$$I_{truth}$$$ are resampled on non-Cartesian coordinates $$$c_{i}$$$ , denoted as $$$k_{non-c}$$$. This is done by convolving $$$k_{cartesian}$$$ with a 3D Gaussian kernel $$$H$$$. Then the sampled k-space data is density compensated and goes through the inverse NUFFT operator to reconstruct an image. A loss between the reconstruction $$$I_{opt}$$$ and $$$I_{truth}$$$ can subsequently be calculated and backpropagated to the radial trajectory coordinates (red dashed arrows). The viability of our method is guaranteed by the fact that the loss function, NUFFT and iNUFFT are all differentiable. We use Pytorch [5] and Sigpy [6] to execute this differentiation efficiently with a GPU accelerated NUFFT and its adjoint. The optimizer used for gradient descent steps was Adam with a learning rate of 1e-4.Loss function: The loss functions we used were mean squared error (MSE) and a learned loss based on radiologists preference of images that has been developed in the group [7].
Optimization on digital phantoms: Radial coordinates were trained to produce better reconstructed images “acquired” from ground truth images of a homogeneous cylindrical phantom as well as in-vivo brain datasets acquired using MPnRAGE [8] and PCVIPR [9]. The optimization was performed on a single case as well as on a cohort of 10 cases. We optimized for both isotropic field of view (FOV) of 256 x 256 x 256 mm and anisotropic FOV with 70 and 50 mm of S/I coverage.
Image acquisition: Phantom and volunteer scans of isotropic and anisotropic FOVs of 256 x 256 x 256mm and 50 x 256 x 256 mm were conducted on a 3.0T scanner with a fast gradient echo sequence of 10,992 projections, TR=20 ms, flip angle=14 $$$^\circ$$$, isotropic resolution=1 mm.
Voronoi areas: Partitions of the sphere surface of k-space around projection vectors are calculated as a sampling uniformity metric.
Results
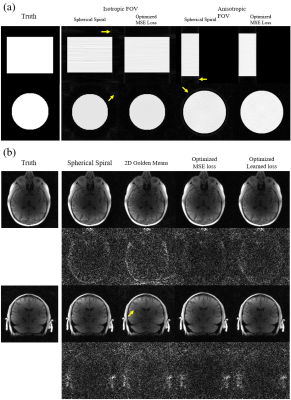
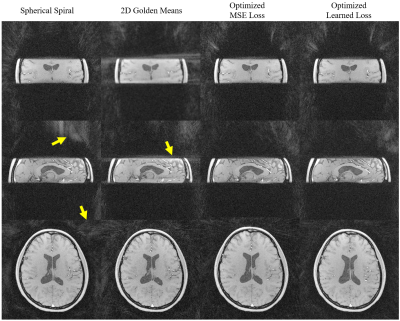
Example optimization results for the cylinder and the brain datasets are shown in Fig 2. As indicated by the arrows, the optimized trajectories were able to generate images with less streaking artifacts and incoherent noise in both the cylinder and the brain than spherical spiral and 2D golden means, regardless of the loss function and the shape of the FOV.The phantom and volunteer scans (Fig 3,4) agree well with the simulation that the optimized trajectories produced images with less noise and more contrast in general.
We also calculated the Voronoi areas around each projection vector to assess the sampling uniformity, listed in Fig 5. Although the spherical spiral has lower standard deviation of the Voronoi areas, it has more dramatic dependence on the polar and azimuthal angles, which could explain some of the artifacts shown in the simulations and the scans.
Discussion and conclusion
We demonstrated that image quality can be used as a metric for 3D radial trajectory optimization. With the autograd framework of pytorch, we were able to approach this problem as a first order optimization problem and obtain images with lower MSE loss and higher radiologists preference score, which were validated in phantom and volunteer scans.Voronoi areas are often used as a sampling uniformity metric. However, as is shown in the table in Fig 5, trajectories optimized based on image quality tend to have larger Voronoi area standard deviation, yet the image quality in digital phantoms and in vivo scans are higher. This confirms our hypothesis that optimizing sampling uniformity may not always lead to the goal of better imaging.
In summary, we present a flexible framework for trajectory optimization, which could be applied to other parameterizable non-Cartesian trajectories, leading to MR of higher image quality and efficiency.
Acknowledgements
We gratefully acknowledge research support from GE Healthcare and funding support from the UCSF/UW grant NIH/NHLBI-R01HL13696.References
[1] H. K. Song, L. Dougherty, and M. D. Schnall, “Simultaneous acquisition of multiple resolution images for dynamic contrast enhanced imaging of the breast,” Magn. Reson. Med., vol. 46, no. 3, pp. 503–509, Sep. 2001, doi: 10.1002/mrm.1220.
[2] R. W. Chan, E. A. Ramsay, C. H. Cunningham, and D. B. Plewes, “Temporal stability of adaptive 3D radial MRI using multidimensional golden means,” Magn. Reson. Med., vol. 61, no. 2, pp. 354–363, 2009, doi: 10.1002/mrm.21837.
[3] D. Piccini, A. Littmann, S. Nielles‐Vallespin, and M. O. Zenge, “Spiral phyllotaxis: The natural way to construct a 3D radial trajectory in MRI,” Magn. Reson. Med., vol. 66, no. 4, pp. 1049–1056, 2011, doi: https://doi.org/10.1002/mrm.22898.
[4] C. Tang, L. Eisenmenger, S. Kecskemeti, and K. M. Johnson, “Acoustic and sampling optimization of 3D Radial MRI using neural network optimization,” presented at the ISMRM 2021, May 2021.
[5] A. Paszke et al., “PyTorch: An Imperative Style, High-Performance Deep Learning Library,” Adv. Neural Inf. Process. Syst., vol. 32, pp. 8026–8037, 2019.
[6] “(ISMRM 2019) SigPy: A Python Package for High Performance Iterative Reconstruction.” http://archive.ismrm.org/2019/4819.html (accessed Dec. 16, 2020).
[7] K. M. Johnson, L. Eisenmenger, P. Turski, and Leonardo. Rivera-Rivera, “Crowdsourced Quality Metrics for Image Reconstruction using Machine Learned Ranking,” presented at the ISMRM 2019, May 2019.
[8] S. Kecskemeti, A. Samsonov, S. A. Hurley, D. C. Dean, A. Field, and A. L. Alexander, “MPnRAGE: A technique to simultaneously acquire hundreds of differently contrasted MPRAGE images with applications to quantitative T1 mapping,” Magn. Reson. Med., vol. 75, no. 3, pp. 1040–1053, 2016, doi: 10.1002/mrm.25674.
[9] T. Gu et al., “PC VIPR: A High-Speed 3D Phase-Contrast Method for Flow Quantification and High-Resolution Angiography,” Am. J. Neuroradiol., vol. 26, no. 4, pp. 743–749, Apr. 2005.
Figures