4997
Fast full-wave patient-specific field simulations in seconds with MARIE 2.0
Georgy Guryev1, Eugene Milshteyn2,3, Ilias I Giannakopoulos4,5, Elfar Adalsteinsson1,6,7, Lawrence L. Wald2,3,7, and Jacob K White1
1Electrical Engineering and Computer Science, Massachusetts Institute of Technology, Cambridge, MA, United States, 2Department of Radiology, Massachusetts General Hospital and Harvard Medical School, Athinoula A. Martinos Center for Biomedical Imaging, Charlestown, MA, United States, 3Harvard Medical School, Boston, MA, United States, 4Center for Advanced Imaging Innovation and Research (CAI2R), Department of Radiology, New York University Grossman School of Medicine, New York, NY, United States, 5The Bernard and Irene Schwartz Center for Biomedical Imaging (CBI), Department of Radiology, New York University Grossman School of Medicine, New York, NY, United States, 6Institute for Medical Engineering and Science, Massachusetts Institute of Technology, Cambridge, MA, United States, 7Harvard-MIT Division of Health Sciences Technology, Cambridge, MA, United States
1Electrical Engineering and Computer Science, Massachusetts Institute of Technology, Cambridge, MA, United States, 2Department of Radiology, Massachusetts General Hospital and Harvard Medical School, Athinoula A. Martinos Center for Biomedical Imaging, Charlestown, MA, United States, 3Harvard Medical School, Boston, MA, United States, 4Center for Advanced Imaging Innovation and Research (CAI2R), Department of Radiology, New York University Grossman School of Medicine, New York, NY, United States, 5The Bernard and Irene Schwartz Center for Biomedical Imaging (CBI), Department of Radiology, New York University Grossman School of Medicine, New York, NY, United States, 6Institute for Medical Engineering and Science, Massachusetts Institute of Technology, Cambridge, MA, United States, 7Harvard-MIT Division of Health Sciences Technology, Cambridge, MA, United States
Synopsis
It was recently demonstrated that the combination of fast low-resolution tissue mapping and fast voxel-based field simulation can be used to perform a patient-specific MR safety check in minutes[4,5].However,field simulation required several of those minutes,making it too slow to perform the dozens of simulations that would be needed for patient-specific optimization.In this abstract we describe a compressed-perturbation-matrix technique that nearly eliminates the computational cost of including complex coils (or coils+shields) in voxel-based field simulation of tissue,thereby reducing simulation time from minutes to seconds.The approach is demonstrated on a wide variety of head+coil and head+coil+shield configurations,using the latest implementation of MARIE2.0.
Introduction
In [2], we showed that the main performance bottleneck in MARIE (the open-source MR field simulator) was associated with the cost of computing the interaction between a complicated RF coil and a realistic human body model, and we used a precorreted FFT (pFFT) algorithm to reduce that cost. The pFFT algorithm proved very effective when the RF coil was tight to the body, but was quite inefficient when the coil, or coil plus shield, was distant from the tissue domain. To obtain an efficient representation of the coil-body coupling, the pFFT expands the voxelized grid from just the body to both the coil and body, an increase in computational domain that becomes prohibitively expensive for large coil structures (e.g. body transmit coils with a shield). Additionally in [2], we represented the coil and the tissue currents as explicit unknowns in an iterative method for equation solution. The difference in scale between currents in the coil and currents in the body interfered with iterative method convergence, along with making convergence difficult to detect.Methodology
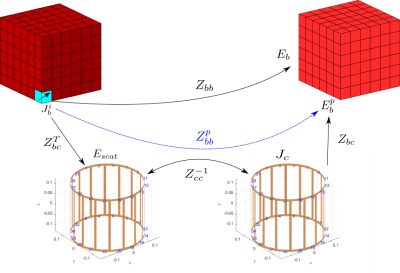
To address the shortcomings associated with the pFFT method and to enable patient-specific simulations with complex RF coils of arbitrary dimensions in seconds, we present the basis-based perturbation approach. To avoid the false convergence of the iterative methods while keeping the iteration count low, we solve the EM problem for the equivalent tissue currents, and then compute coil currents as a post-processing step. Second, the body-specific problem in the presence of the RF coil naturally decomposes into the direct tissue-to-tissue and the perturbation tissue-to-tissue operators. The direct term describes what fields are produced within the body by an equivalent tissue current in a given voxel in the absence of the coil; this operator is tissue-dependent, however could be efficiently compressed and applied as shown in [1]. The perturbation term describes how tissue voxels interact with each other through the medium of the coil (see Fig.1) and is agnostic to the material properties of the patient (tissue currents-to-coil currents-to-tissue fields perturbation operator). This operator could be precomputed for a given RF coil and a bounding box once when a new coil geometry is introduced to the MARIE 2.0.Electric and magnetic perturbation operators
Note, that the perturbation operator is a composition of three consecutive mappings: first, the tissue currents are mapped to the electric fields, incident on the coil; then the incident electric fields are mapped to the perturbation currents induced on the surface of the coil; finally, the perturbation currents are mapped back to the electric fields within the tissue. Thus, the perturbation operator is a result of two coil-tissue coupling operators, which in the MRI context are of a low-rank nature and could be efficiently approximated with standard low-rank factorization techniques (truncated SVD, CUR/Cross approximation, Tucker or Tensor Train factorizations, etc.)[6]. This suggests that the resulting perturbation operator would have a rank much lower than the tissue-to-coil coupling due to the squaring effect of the decay of the singular values and, therefore, allows an even more compact representation and efficient application of the perturbation operator. Moreover, unlike the pFFT, this approach does not require the extension of the voxelized domain to cover the RF coil (and shield) and hence is suitable for both large and tight coil geometries. The same perturbation approach could be used to find the magnetic fields. The total magnetic field could be represented as a superposition of the incident (coil-to-tissue) and scattered (tissue-to-tissue) magnetic fields. The scattered field is efficiently computed as in [1], while the incident field could be expressed in terms of tissue currents with the tissue-to-tissue operator that maps tissue currents to magnetic fields within the tissue.Results
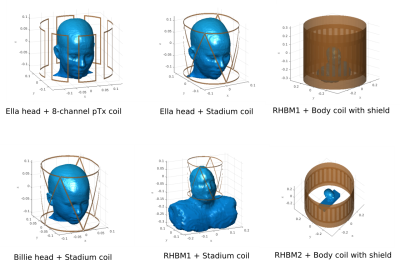
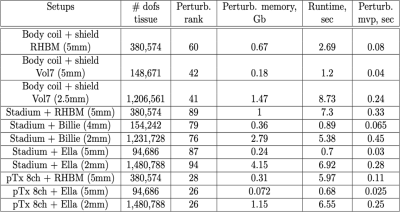
The numerical simulations with the basis-based perturbation approach were carried out for several coil and body models, shown in Figure 2. The corresponding results with memory footprints and typical runtimes are shown in Figure 3. Figure 4 demonstrates the typical rank and simulation times for the 8-channel coil and Billie model at different resolutions while Figure 5 shows the resulting electric and magnetic field patterns. From the presented data, one can see that the rank of the perturbation matrix remains the same at different resolutions, while the perturbation matrix-vector product becomes insignificant. The perturbation rank for all our examples remained low, 25-94 (even though the dimensions of the perturbation matrix is in the millions). For comparison, typical tissue-to-coil ranks as high as 770, so the perturbation matrix is much more efficient.Discussion
In this work we have presented a body-agnostic basis-based perturbation approach that allows us to carry out the patient-specific EM simulations in seconds. The tissue-to-tissue basis is coil-specific and has to be generated for every new coil geometry, NOT every new patient, and the basis construction requires several hours or less. All quantities of interest (electric and magnetic fields, network parameters, SNR, SAR) are computed without ever storing the tissue-to-coil coupling operator in memory.Acknowledgements
The authors graciously acknowledge the support of the Skolkovo Institute of Technology Next Generation Program, NIH 5R01EB006847R01EB006847References
[1] Villena, Jorge Fernández, et al. "Fast electromagnetic analysis of MRI transmit RF coils based on accelerated integral equation methods." IEEE Transactions on Biomedical Engineering 63.11 (2016): 2250-2261.
[2] Guryev, G. D., et al. "Fast field analysis for complex coils and metal implants in MARIE 2.0." ISMRM (2019).
[3] Phillips, Joel R., and Jacob K. White. "A precorrected-FFT method for electrostatic analysis of complicated 3-D structures." IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems 16.10 (1997): 1059-1072.
[4] Eugene Milshteyn, et al. “Approaching Real-Time Patient-Specific SAR Calculation for Parallel Transmission at 7 Tesla”, ISMRM (2021)
[5] Eugene Milshteyn, et al., “Individualized SAR calculations using computer vision‐based MR segmentation and a fast electromagnetic solver”, Magnetic Resonance in Medicine 85.1 (2021):429-443
[6]Ilias Giannakopoulos, et. al., “Compression of volume-surface integral equation matrices via Tucker decomposition for magnetic resonance applications”, IEEE Transactions on Antennas and Propagation (2021)
Figures
Figure 1: The tissue-to-tissue perturbation operator maps volumetric current in the i-th voxel to the fields in all tissue voxels through the medium of the coil
Figure 2. Coil-body model geometries. The RF coils are tuned and matched ( coils are represented with the triangular mesh) and loaded with the voxelized realistic human head/body models
FIgure 3. Results for the perturbation approach with truncation and solver tolerances set to 1e-3 (piecewise constant basis). Stadium coil has 10,928 unknowns, Body coil + shield has 36,423 unknowns
Figure 4. The breakdown of the perturbation rank and simulation times for the 8-channel pTx coil (3904 unknowns) and Billie models at different resolutions (piecewise constant basis functions)
Figure 5 - The Electric and Magnetic field patterns (axial cut) in the Billie head model at 4mm, 2mm and 1mm resolutions, respectively, generated with the 8-channel ptx coil when 1V excitation was applied to the first port. The presented results were obtained at 7T with a piecewise constant (PWC) basis defined within the tissue domain.
DOI: https://doi.org/10.58530/2022/4997