Introduction

Episodic memory loss is a hall mark symptom in Alzheimer’s disease (AD). Task-based fMRI has the capability to detect abnormal brain activations during episodic memory tasks at a prodromal stage before clinical dementia onset ^1,2. However, the signal-to-noise ratio (SNR) in fMRI data is usually low, especially in the targeted memory activation regions, the medial temporal lobe (MTL). To improve the SNR, isotropic Gaussian smoothing with a preselected full-width-half-maximum (FWHM) has been widely adopted as an fMRI preprocessing step³. However, using a single FWHM across the whole brain for Gaussian smoothing disregards the regional cortical differences, and introduces smoothing artifacts to the fine-mapping regions such as MTL⁴. In this study, we propose a method that optimizes voxel-wise FWHMs for isotropic Gaussian smoothing to improve the specificity while maintaining the sensitivity in subject-level activation detection during fine-mapping fMRI tasks. Directional steerable filters, as spatially adaptive alternatives to an isotropic Gaussian filter, have also been explored for their advantages in capturing directional activations⁵.

Methods

Model. Table. 1 illustrates our proposed method. For a given center voxel, let Y (takes the dimension [t, W_x, W_y, W_z]) be a matrix representing fMRI time courses of voxels from its 3D local neighborhood; and G be the filter with the current FWHM used to smooth this local neighborhood; window sizes [W_x, W_y, W_z] are determined from the current FWHM (detailed in Table 1). The smoothed time series of the center voxel can then be represented as Y'=YxG; and take the dimension of [t,1] and for an isotropic Gaussian filter and [t,7] for 7 steerable filters. Let X=(x₁,x₂,...,x_n) take the dimension [t, n] and represent n functions used to model the BOLD response. A sequential quadratic programming solver⁶ was further adopted to optimize the FWHM of each voxel through minimizing the error term in the general linear model (GLM) for an isotropic-Gaussian-filter-smoothed time series (Y' takes the dimension [t,1] and obj_FWHM=||YG_iso - Xβ||²), and constrained canonical correlation analysis model⁷ for steerable-filters-smoothed time series (Y' takes the dimension [t,7] and obj_FWHM=||YG_stα- Xβ||²), as detailed in Table 1. Imaging. fMRI data (TR/TE/resolution= 2s/30ms/1.7x1.7x5mm³, 25 slices, coronal oblique, 288-time frames) from 16 subjects each consisting of a resting-state data set and an episodic memory task data set were analyzed. The memory task involved viewing faces paired with occupations and contained instruction, encoding, recognition and control periods. Simulated data: 500 5x5 neighborhoods with active center voxels and 500 neighborhoods with inactive center voxels for 16 subjects, simulated in Zhuang et al⁸, are reused here. Briefly, the distribution of active neighbors in each local neighborhood followed the empirical distribution of real fMRI data analyzed with the univariate method. Time-series for simulated neighborhoods were obtained from neighborhoods in real data with the same activation patterns (both resting-state and task fMRI). Wavelet-resampled resting-state time-series were added to the task time-series with different noise fractions to simulate time courses at different noise levels. Analysis. GLM with various isotropic Gaussian smoothing levels (FWHM=0mm,2mm,4mm,6mm,8mm) and the proposed methods were applied to both simulated and real fMRI data, respectively. Voxel-wise activation map for contrast encoding v/s control was computed to detect brain activation in each method. The conventional receiver operating characteristic (ROC) method and the recovered ROC⁹ method were used to evaluate the performance of each method in simulated data (with known ground truth) and real fMRI data, respectively.

Results

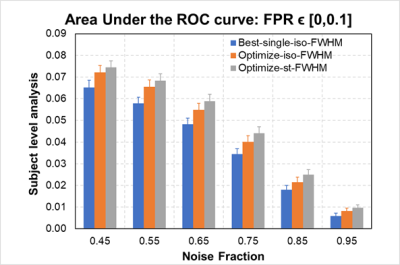
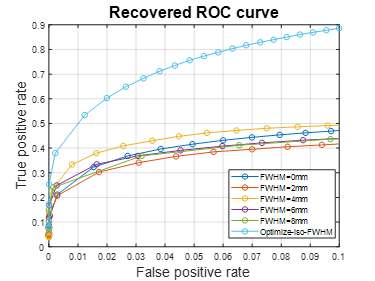
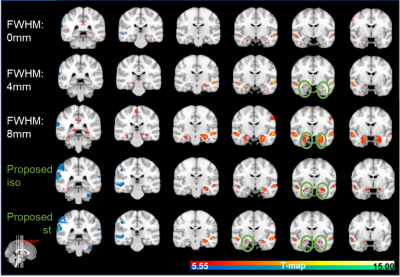
Fig.1 plots the area under the ROC curves (AUC) for simulated data with noise fractions from 0.45 to 0.95, integrated over false positive rate (FPR) from 0 to 0.1 and averaged over 16 subjects. As shown in Fig. 1, in terms of AUC in the low FPR range, optimizing FWHM for isotropic Gaussian filter significantly improves the model performance in activation detection over GLMs with time series smoothed using a single FWHM. Optimizing FWHM for steerable filters further boosts the AUC for another 10.79%±5.37% on average. Fig. 2(A) plots the recovered ROC curves for activation maps for contrast “Encoding vs. Control” from a representative subject obtained using GLM on time series smoothed with various single FWHMs and with optimized FWHM voxel-wisely. At a given FPR, optimizing FWHM for isotropic Gaussian filter (light blue curve in Fig. 2) significantly increases the true positive rate (TPR) over other methods. Furthermore, activation maps for this contrast thresholded at FWE p≤0.05 are shown in Fig. 3. As indicated by green circles in Fig. 3, optimizing FWHM for both isotropic Gaussian filter and steerable filters enable the detection of activation in the bilateral hippocampus without producing significant smoothing artifacts.

Discussion and conclusion

Our proposed methods are targeted at finding the most appropriate FWHM for the smoothing filters at every voxel. By incorporating the smoothing step into the optimization problem, the proposed methods were able to more accurately detect both simulated activations and medial temporal lobe activations during a real fMRI episodic memory task.

Acknowledgements

This study is supported by the National Institutes of Health (grant 1RF1AG071566, P20GM109025 and P20AG068053), a private grant from the Peter and Angela Dal Pezzo funds, a private grant from Lynn and William Weidner, a private grant from Stacie and Chuck Matthewson, and the young scientist award at Cleveland Clinic Lou Ruvo Center for Brain Health (Keep Memory Alive Foundation).