4971
Subcortical Parcellation of the Human Brain via Automated Voxel Annotation with Fiber Clusters
Ye Wu1, Sahar Ahmad1, and Pew-Thian Yap1
1Department of Radiology and Biomedical Research Imaging Center (BRIC), University of North Carolina at Chapel Hill, Chapel Hill, NC, United States
1Department of Radiology and Biomedical Research Imaging Center (BRIC), University of North Carolina at Chapel Hill, Chapel Hill, NC, United States
Synopsis
Connectivity-based parcellation of subcortical structures typically relies on the pre-parcellation of the cortex. Here, we propose an unsupervised data-driven approach for subcortical parcellation based on diffusion tractography without relying on the annotation of cortical regions or fiber tracts.
Introduction
Subcortical structures are a group of interconnected gray matter structures lying deep beneath the white matter and include the diencephalon, pituitary gland, limbic structures, and the basal ganglia1,2. These structures are involved in complex processes such as cognition, movement, memory, learning, emotion, and homeostasis. Accurate parcellation of the brain subcortex facilitates the investigation of the contributions of subcortical nuclei to human cognitive skills and social behaviors. Subcortical parcellation can be based on the connectivity profiles of subcortical voxels in relation to cortical gray matter, often determined using diffusion tractography3–6. However, annotation inaccuracy of the cortex or the fiber tracts can affect subcortical parcellation. To overcome this limitation, we propose a data-driven approach for subject-specific subcortical parcellation without relying on cortical or tract annotations.Materials and Methods
We utilized the anatomical and diffusion MRI data of 12 subjects from the Human Connectome Project Young Adult (HCP-YA) study7. The subjects were scanned between 24 and 34 years ($$$30.5 \pm 3.23$$$) of age using a Siemens 3T Prisma MRI scanner. Diffusion-weighted images were acquired with $$$(1.25 ~mm)^3$$$ isotropic voxel resolution along 270 noncollinear gradient directions with $$$b=1000,2000,3000 ~s/mm^2$$$. The data were minimally preprocessed with the standard HCP processing pipeline8.Our approach for population subcortical parcellation involves (i) streamline clustering9; (ii) voxel annotation based on streamline clusters; and (iii) sparse non-negative matrix factorization (NMF) for subcortical parcellation3.
We start with whole-brain tractography using asymmetric fiber orientation distribution functions (AFODFs) to better capture complex axonal configurations (e.g., bending, fanning, and crossing) and to mitigate gyral bias for better cortico-cortical connectivity10,11. Fiber streamlines are generated by successively following the local directions determined from the AFODFs12. Whole-brain tractography is performed with 64 random seeds per voxel, resulting in approximately 100 million streamlines, but only streamlines that traverse subcortical regions are retained.
$$$\textbf{Unsupervised Bilateral Fiber Clustering.}$$$ We warp a random subset of the fiber streamlines of each subject to the MNI atlas space with affine and non-linear transforms estimated between the subject anatomical scan and the atlas. Spatially normalized streamlines of all subjects are combined for population-level fiber clustering using an automated unsupervised fiber clustering method. The streamlines are mapped to a Hilbert space via parameterization as coefficients of a cosine series13 and then grouped into $$$K$$$ clusters via $$$K$$$-medoids clustering9. Streamlines in both cerebral hemispheres are clustered bilaterally for consistency and robustness.
$$$\textbf{Voxel Annotation with Streamline Clusters.}$$$ We encode the relationship between the $$$K$$$ streamline clusters and the $$$N$$$ voxels using a matrix $$$C=(c_{ki})$$$, where $$$c_{ki}=1$$$ if more than 2 streamlines in cluster $$$k$$$ traverse voxel $$$i$$$, otherwise $$$c_{ki}=0$$$.
$$$\textbf{Sparse NMF parcellation.}$$$ Sparse NMF has been successfully applied for whole-brain parcellation3. The non-negativity constraint in NMF improves interpretability and robustness14. We decompose the encoding matrix as above into $$$M$$$ components using sparse NMF, resulting in a component matrix $$$H$$$ and the respective component coefficients. Each voxel is assigned to the component corresponding to the largest coefficient in the coefficient vector of the voxel, resulting in an initial parcellation map $$$S$$$ with $$$M$$$ parcels. Finally, We correct for isolated voxels by incorporating information from neighboring voxels by updating $$$S$$$ using constraints from adjacency voxels3.
We evaluated our parcellation method using a specificity score that characterizes the distance between the parcels. For each $$$M$$$, we encode in matrix $$$Q$$$ the cosine distances between component kernels. The specificity score is then defined as $$$\frac{D}{M}$$$, where $$$D$$$ is the principal component eigenvalue computed using singular value decomposition. A lower score indicates higher specificity, signifying better parcellation.
Results
We evaluated the parcels specificity of streamline clustering with different numbers of clusters. We found that $$$K=500$$$ is sufficient for capturing better specificity (Fig. 1). Subcortical parcellation results shown in Fig. 2 indicate great consistency with existing studies.Acknowledgements
This work was supported in part by the United States National Institutes of Health (NIH) through grants MH125479, EB008374, and EB006733.References
1. Haines DE. Neuroanatomy: An Atlas of Structures, Sections, and Systems. Lippincott Williams & Wilkins; 2004.2. Augustine JR. Human Neuroanatomy. Academic Press; 2008.
3. Wu Y, Ahmad S, Yap P-T. Highly Reproducible Whole Brain Parcellation in Individuals via Voxel Annotation with Fiber Clusters. Medical Image Computing and Computer Assisted Intervention – MICCAI 2021. Springer International Publishing; 2021. p. 477–486.
4. Mars RB, Jbabdi S, Sallet J, et al. Diffusion-Weighted Imaging Tractography-Based Parcellation of the Human Parietal Cortex and Comparison with Human and Macaque Resting-State Functional Connectivity. Journal of Neuroscience 2011. p. 4087–4100.
5. Huang H, Zhang J, Jiang H, et al. DTI Tractography based Parcellation of White Matter: Application to the Mid-sagittal Morphology of Corpus Callosum. Neuroimage. 2005;26:195–205.
6. Tomassini V, Jbabdi S, Klein JC, et al. Diffusion-Weighted Imaging Tractography-Based Parcellation of the Human Lateral Premotor Cortex Identifies Dorsal and Ventral Subregions with Anatomical and Functional Specializations. Journal of Neuroscience 2007. p. 10259–10269.
7. Sotiropoulos SN, Jbabdi S, Xu J, et al. Advances in diffusion MRI acquisition and processing in the Human Connectome Project. Neuroimage. 2013;80:125–143.
8. Glasser MF, Sotiropoulos SN, Wilson JA, et al. The minimal preprocessing pipelines for the Human Connectome Project. Neuroimage. 2013;80:105–124.
9. Wu Y, Hong Y, Ahmad S, Lin W, Shen D, Yap P-T. Tract Dictionary Learning for Fast and Robust Recognition of Fiber Bundles. Medical Image Computing and Computer Assisted Intervention – MICCAI 2020. Springer, Cham; 2020. p. 251–259.
10. Wu Y, Lin W, Shen D, Yap P-T, Consortium UBCP, Others. Asymmetry Spectrum Imaging for Baby Diffusion Tractography. International Conference on Information Processing in Medical Imaging. Springer, Cham; 2019. p. 319–331.
11. Wu Y, Hong Y, Feng Y, Shen D, Yap P-T. Mitigating Gyral Bias in Cortical Tractography via Asymmetric Fiber Orientation Distributions. Med Image Anal. Elsevier; 2020;59:101543.
12. Wu Y, Hong Y, Ahmad S, et al. Globally Optimized Super-Resolution of Diffusion MRI Data via Fiber Continuity. Medical Image Computing and Computer Assisted Intervention – MICCAI 2020. Springer, Cham; 2020. p. 260–269.
13. Chung MK. Cosine Series Representation. arXiv [stat.CO] 2021.
14. Mairal J, Bach F, Ponce J, Sapiro G. Online learning for matrix factorization and sparse coding. J Mach Learn Res [online serial]. jmlr.org; 2010;11.
15. Adler DH, Wisse LEM, Ittyerah R, et al. Characterizing the human hippocampus in aging and Alzheimer’s disease using a computational atlas derived from ex vivo MRI and histology. Proc Natl Acad Sci U S A. 2018;115:4252–4257.
16. Tian Y, Margulies DS, Breakspear M, Zalesky A. Topographic organization of the human subcortex unveiled with functional connectivity gradients. Nat Neurosci. 2020;23:1421–1432.
Figures
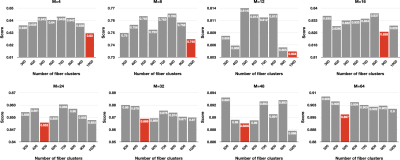
Fig. 1. The effects of streamline clustering in association with the numbers of clusters.
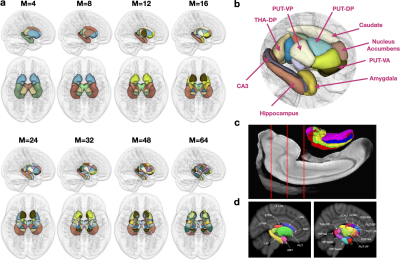
Fig. 2. Population parcellation. (a) Parcellation examples for different values of M. (b) Close-up view of the subregions parcellated with M=16. (c) Parcellation of the hippocampus from Adler et al.15. (d) Parcellation of the subcortex from Tian et al.16.
DOI: https://doi.org/10.58530/2022/4971