4871
Motion-Corrected Multiphase Imaging with Steady-state Free Precession for Free-breathing 3D Coronary Angiography1Department of Bioengineering, Stanford University, Stanford, CA, United States, 2Magnetic Resonance Systems Research Lab (MRSRL), Department of Electrical Engineering, Stanford University, Stanford, CA, United States, 3Department of Radiology, Stanford University, Stanford, CA, United States
Synopsis
For free-breathing 3D coronary angiography, we consider a new multiphase acquisition that consists of a series of short imaging blocks to reduce motion blur in the acquisition window. However, this approach poses two challenges: (1) because the alterations of readout gradient waveforms become large due to the shortened imaging window, eddy current artifacts appear in steady-state free precession imaging, and (2) motion among cardiac phases needs to be addressed. In this work, we propose a new ordering scheme to establish smooth transitions between conic interleaves. Phase-to-phase motion is estimated using self image-based navigators and corrected by motion-based reconstruction.
Introduction
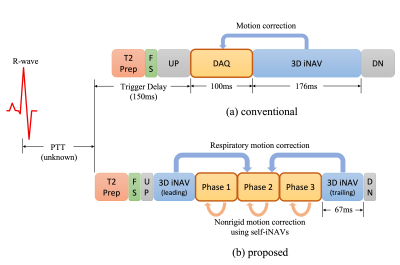
In free-breathing coronary angiography using a segmented acquisition, it is often assumed that cardiac motion is frozen during the acquisition window set by a trigger delay. In fact, the heart moves across all cardiac cycles$$$^{1, 2}$$$, and the optimal trigger delay may be different for different coronary arteries$$$^{1}$$$.To reduce motion blur in the acquisition window and extend the total acquisition time, we consider a new multiphase acquisition that consists of a series of short imaging blocks (Figure 1). For each cardiac phase, data are collected using a segmented cones trajectory that sparsely covers k-space. This approach, however, poses two challenges: (1) because the alterations of readout gradient waveforms become large due to the shortened imaging window, eddy current artifacts appear in steady-state free precession (SSFP) imaging, and (2) motion among cardiac phases needs to be addressed.
In this work, ordering spirals are introduced to establish the smooth transitions between conic interleaves. Double averaging (dAVE) $$$^3$$$ is employed for further eddy current compensation. Beat-to-beat translational motion is corrected using 3D image-based navigators (iNAVs)$$$^4$$$, and subsequently self iNAVs of cardiac and respiratory phases are reconstructed to estimate nonrigid motion. Image-space gridding$$$^5$$$ is used to compute forward and adjoint of nonrigid transforms, and motion-corrected reconstruction is achieved by solving an optimization problem.
A New Ordering Scheme for 3D Cones Trajectory
The cones trajectory can be obtained by rotating template interleaves that sit on distinct conic surfaces$$$^6$$$. The rotation angles about the z-axis and polar angles of cones can be determined by discretization of a spiral on the unit sphere$$$^6$$$:$$\begin{align} \begin{split}\label{eq:design_spiral} x[u] &= \cos \beta(u) \sin \phi(u)\\ y[u] &= \sin \beta(u) \sin \phi(u)~~~~~~~(1)\\ z[u] &= \cos \phi(u), \end{split}\end{align}$$
where $$$u \in (0, 1)$$$ denotes the control variable, and $$$\beta(u)$$$ and $$$\phi(u)$$$ represent the speeds along the azimuthal and polar directions, respectively$$$^6$$$. We refer to (1) as "design spiral."
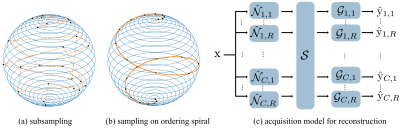
An intuitive discretization method for multiphase acquisition is to perform subsampling over uniformly sampled $$$u[i]$$$ (Figure 2(a)). The resulting trajectory, however, is likely distributed in a disordered fashion, which often produces severe eddy current artifacts in SSFP sequences. Here, we introduce a new spiral, named "ordering spiral," on the unit sphere:
$$\begin{align} \begin{split}\label{eq:ordering_spiral} x[u] &= \cos \xi(u) \sin \phi(u)\\ y[u] &= \sin \xi(u) \sin \phi(u)~~~~~~~~~~(2)\\ z[u] &= \cos \phi(u), \end{split}\end{align}$$
where $$$\xi(u) = 2 \pi u N$$$, and N denotes the number of turns in the azimuthal direction. Smooth transitions between interleaves can be established by sampling on intersections of design and ordering spirals (Figure 2(b)). For further eddy current compensation, dAVE$$$^3$$$ is incorporated.
Nonrigid Motion-Corrected Reconstruction
Beat-to-beat 3D translational motion is measured using 3D iNAVs$$$^4$$$ and corrected in k-space raw data. To estimate phase-to-phase motion and residual respiratory motion, the corrected data are binned to reconstruct self iNAVs of cardiac and respiratory phases. Finally, the motion-corrected reconstruction is achieved by solving the following optimization problem:$$\begin{align} \arg \min _{\mathrm{x}} \frac{1}{2} \sum_{c, r} ||\hat{\mathrm{y}}_{c, r} - \mathcal{G}_{c, r} ~ \mathcal{S} ~ \hat{\mathcal{N}}_{c, r} ~ \mathrm{x}||_2^2 + \lambda ||\mathcal{W}\mathrm{x}||_1,\end{align}$$
where c and r represent indices for cardiac and respiratory phases, $$$\mathrm{x}$$$ and $$$\hat{\mathrm{y}}$$$ denote the image to be reconstructed and corrected k-space data, $$$\mathcal{S}$$$, $$$\mathcal{G}$$$, $$$\hat{\mathcal{N}}$$$, and $$$\mathcal{W}$$$ represent the coil sensitivity, k-space inverse gridding, nonrigid transform, and sparsifying transform, respectively. The forward and adjoint of nonrigid transform can be computed using image-space gridding$$$^5$$$.
Methods
Data were acquired on a 1.5T GE Signa scanner using an 8-channel cardiac coil. An ATR-bSSFP sequence$$$^{7,8}$$$ was prescribed with the following parameters: TE=0.7ms, TR=4.8ms, flip angle=65$$$^\circ$$$, number of heartbeats=600. During each heartbeat three cardiac phases were collected using the segmented high-resolution (1.2mm) variable-density cones trajectory$$$^6$$$ with the proposed ordering scheme. The low-resolution (5mm) variable-density cones interleaves were played out before and after the imaging blocks for 3D iNAVs$$$^{4, 8}$$$. The acquisition window of each imaging block was 67.2ms.Results and Discussion
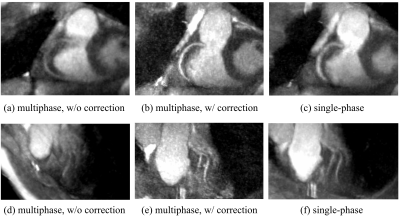
A ball phantom was used to assess eddy current artifacts produced by different ordering schemes. The combination of the proposed ordering scheme with the dAVE$$$^3$$$ exhibited reduced artifact than other approaches (Figure 3).Figure 4 shows images of the right coronary artery (RCA) and left anterior descending artery (LAD). The motion-corrected images were much sharper than uncorrected results, which demonstrates the feasibility of our nonrigid motion-corrected reconstruction. Compared to the single-phase acquisition, the proposed approach displayed better vessel depiction for the RCA, and comparable performance for the LAD.
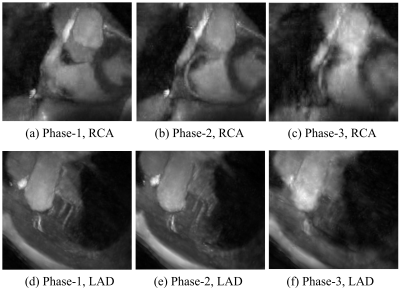
In Figure 5, substantial cardiac movement was observed near the RCA in the first cardiac phase, whereas little motion appeared in the later phases. In contrast, the LAD appears sharp in the first cardiac phase. This result is consistent with Hofman et al.'s study$$$^1$$$ that indicated that the optimal acquisition window for the LAD may be earlier than that for the RCA.
As illustrated in Figure 1, the acquisition window of the single-phase approach spans only the first and a small portion of the second cardiac phase of the multiphase sequence. The result in Figure 5 suggests that the single-phase approach missed the optimal acquisition windows for the RCA, whereas it was captured by the proposed multiphase acquisition thanks to its extended imaging duration. Therefore, we expect improved robustness against subject variability with the proposed multiphase approach.
Acknowledgements
The authors gratefully acknowledge the support from NIH grant R01 HL127039 and GE Healthcare.References
1. M. B. Hofman, S. A. Wickline, and C. H. Lorenz, "Quantification of in-plane motion of the coronary arteries during the cardiac cycle: implications for acquisition window duration for MR flow quantification," Journal of Magnetic Resonance Imaging, vol. 8, no. 3, pp. 568–576,1998.
2. Y. Wang, R. Watts, I. R. Mitchell, T. D. Nguyen, J. W. Bezanson, G. W. Bergman, and M. R. Prince, "Coronary MR angiography: selection of acquisition window of minimal cardiac motion with electrocardiography-triggered navigator cardiac motion prescanninginitial results," Radiology, vol. 218, no. 2, pp. 580–585, 2001.
3. M. Markl, J. Leupold, O. Bieri, K. Scheffler, and J. Hennig, "Double average parallel steady-state free precession imaging: optimized eddy current and transient oscillation compensation," Magnetic Resonance in Medicine, vol. 54, no. 4, pp. 965–974, 2005.
4. N. O. Addy, R. R. Ingle, J. Luo, C. A. Baron, P. C. Yang, B. S. Hu, and D. G. Nishimura, "3D image-based navigators for coronary MR angiography," Magnetic resonance in medicine, vol. 77, no. 5, pp. 1874–1883, 2017.
5. K. E. Jang, D. G. Nishimura, and S. S. Vasanawala, "Nonrigid Motion-corrected Reconstruction Using Image-space Gridding for Free-breathing Cardiac MRI," in Proceedings of the 29th Annual Meeting of the ISMRM, 2021.
6. K. E. Jang, S. P. Koundinyan, D. G. Nishimura, and S. S. Vasanawala, "Redesigned Variable Density Cones Trajectory for High Resolution MR Imaging," in Proceedings of the 27th Annual Meeting of the ISMRM, 2019.
7. J. Leupold, J. Hennig, and K. Scheffer, "Alternating repetition time balanced steady state free precession," Magnetic Resonance in Medicine, vol. 55, no. 3, pp. 557–565, 2006.
8. H. H. Wu, P. T. Gurney, B. S. Hu, D. G. Nishimura, and M. V. McConnell, Free-breathing multiphase whole-heart coronary MR angiography using image-based navigators and three-dimensional cones imaging," Magnetic resonance in medicine, vol. 69, no. 4, pp. 1083–1093, 2013.
9. M. Uecker, P. Lai, M. J. Murphy, P. Virtue, M. Elad, J. M. Pauly, S. S. Vasanawala, andM. Lustig, "ESPIRiT – an eigenvalue approach to autocalibrating parallel MRI: where SENSE meets GRAPPA," Magnetic resonance in medicine, vol. 71, no. 3, pp. 990–1001, 2014.
10. B. C. Lowekamp, D. T. Chen, L. Ibanez, and D. Blezek, "The design of SimpleITK,", Frontiers in neuroinformatics, vol. 7, p. 45, 2013.
11. T. Vercauteren, X. Pennec, A. Perchant, N. Ayache, et al., "diffeomorphic demons using ITKs finite difference solver hierarchy," The Insight Journal, vol. 1, 2007.
12. A. Beck and M. Teboulle, "A fast iterative shrinkage-thresholding algorithm for linear inverse problems," SIAM journal on imaging sciences, vol. 2, no. 1, pp. 183–202, 2009.
Figures