4867
Distributed memory-efficient deep learning reconstruction for improved SIMBA whole-heart coronary MRI1Department of Electrical and Computer Engineering, University of Minnesota, Minneapolis, MN, United States, 2Center for Magnetic Resonance Research, University of Minnesota, Minneapolis, MN, United States, 3Department of Diagnostic and Interventional Radiology, Lausanne University Hospital and University of Lausanne, Lausanne, Switzerland, 4Advanced Clinical Imaging Technology, Siemens Healthcare AG, Bern, Switzerland, 5Center for Biomedical Imaging, Lausanne, Switzerland
Synopsis
SImilarity-driven Multi-dimensional Binning Algorithm (SIMBA) is a recently proposed technique for identifying motion-consistent clusters in free-running whole-heart MRA acquisitions, where the clusters are subsequently reconstructed using conventional approaches. Physics-guided deep learning (PG-DL) reconstruction has gained popularity with its superior performance at higher acceleration rates and may further improve the image quality of free-running whole-heart MRA in conjunction with SIMBA. However, PG-DL is difficult to apply to 3D non-Cartesian acquisitions due to hardware limitations. In this work we enable distributed memory-efficient PG-DL for large-scale SIMBA datasets, showing preliminary results in which PG-DL improves image quality compared to conventional methods.
INTRODUCTION
SImilarity-driven Multi-dimensional Binning Algorithm (SIMBA1) is a recently proposed physiological motion compensation approach applied to free-running whole-heart MRI. It enables reconstruction of static motion-suppressed datasets without explicit physiological signal extraction or any assumptions regarding cardiac and respiratory frequencies. SIMBA uses a clustering approach to identify readout lines from a kooshball acquisition that are in similar motion states, and reconstructs these bins using conventional methods, such as gridding. Recently, physics-guided deep learning (PG-DL) reconstruction has emerged as a powerful strategy for accelerated MRI, showing improvements on conventional reconstruction approaches2-4. Yet, PG-DL is difficult to apply to 3D large-scale non-Cartesian imaging, due to GPU memory limitations5,6. In this study we adopt various techniques including memory-efficient learning7, Toeplitz method for encoding-decoding operations8 and mixed-precision processing9, along with a distributed learning strategy, to enable fast PG-DL reconstruction of accelerated SIMBA datasets. We pretrain the network on navigator-gated kooshball coronary MRI datasets10, and test on SIMBA clusters, showing good generalization, and improved image quality compared to gridding.METHODS
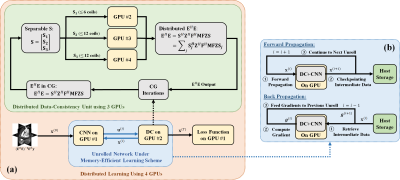
PG-DL Formulation: The inverse problem for regularized MRI reconstruction is\begin{align}
\textrm{arg}\min_{\bf{x}}||\bf{Ex-y}||_2^2 + \mathcal{R}(\bf{x})
\end{align}
where $$$\bf x$$$ is the image of interest, $$$\bf y$$$ is the acquired k-space, $$$\bf E$$$ is the multi-coil encoding operator, and is a regularizer. In PG-DL, an algorithm for solving (1) is unrolled for a fixed number of steps. Each unrolled iteration contains a linear data-consistency (DC) and CNN-based regularizer6.
Memory-Efficient PG-DL for 3D Kooshball: Aiming to overcome hardware limitations, we adopt multiple techniques to enable PG-DL reconstruction of 3D kooshball data: 1) We utilize memory efficient learning for unrolled networks7, which keeps only a single unrolled step on the GPU to reduce memory occupation. 2) We apply the Toeplitz method8 to implement E and its adjoint in data consistency units, which performs point-wise multiplications over a doubled matrix size instead of memory consuming gridding and re-gridding operations. 3) Mixed-precision processing is used in network training to further reduce memory occupation, with no noticeable loss on accuracy9. 4) We distribute the network training on 4 GPUs, where 3 GPUs handle the linear data-consistency step and 1 GPU is responsible for CNN regularizer, as well as loss calculation (Figure 1).
Navigator-Gated Training Set: 6 navigator-gated 3D kooshball coronary MRI datasets were used to train the PG-DL network. These were acquired on a Siemens Magnetom Aera 1.5T scanner using an ECG-triggered T2-prepared, fat-saturated, navigator-gated prototype bSSFP sequence, with relevant parameters: RF excitation angle=90°, resolution=(1.15mm)3, matrix size=1923, FOV=(220mm)3 with 2-fold readout oversampling, TR/TE=3.0/1.52ms, bandwidth=898Hz/Px. A total of 12320 radial projections (sub-Nyquist rate of 5) were acquired in 385 heartbeats with the spiral phyllotaxis pattern10 with one interleaf of 32 projections per heartbeat.
Training Details: Oversampling was removed by cropping the image domain FOV into 2243. Coil sensitivities were estimated using the center Nyquist-sampled region. 10 unrolled steps were used in the PG-DL network. Linear data-consistency is solved using 9 conjugate gradient iterations. A ResNet11 is employed as the CNN regularizer with 3×3×3 convolutions accordingly.
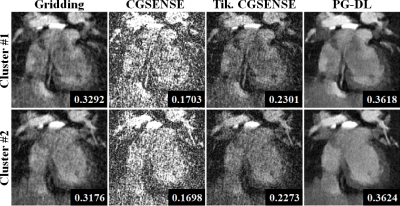
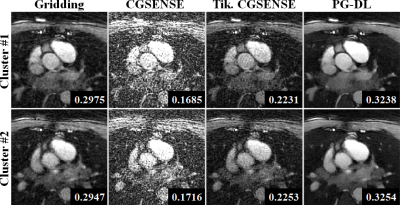
SIMBA Datasets: Two healthy subjects were used for this proof-of-principle study. Examinations were performed with the bSSFP free-running protocol described in12 on a 1.5T clinical MRI system (MAGNETOM Aera, Siemens Healthcare, Erlangen, Germany). Scan time was fixed at 14:17min for an untriggered and ungated acquisition of 126.478 readouts subdivided in 5749 interleaves of 22 readouts each. Main sequence parameters were: RF excitation angle=90°, resolution=(1.15 mm)3, FOV=(220 mm)3, TE/TR=1.56/3.1 ms, readout bandwidth: 898Hz/Px. SIMBA was applied as in the original publication1. Each cluster from the SIMBA datasets was reconstructed individually using four techniques: 1) Gridding reconstruction as the baseline, 2) Unregularized CG-SENSE, 3) Tikhonov-regularized CG-SENSE, 4) PG-DL reconstruction trained on navigator-gated data. Due to the lack of a Nyquist-sampled reference, image quality was evaluated visually, and using a quantitative referenceless blur metric13.
RESULTS
Figure 2 and 3 depict representative reconstructions of two clusters in coronal and axial views, respectively. Due to the relatively high acceleration rate of 6.6 and 4.5 respectively, noticeable artifacts are observed in gridding reconstructions. Unregularized CG-SENSE suffers from noise amplification, while the Tikhonov regularized CG-SENSE displays visual blurring, while also failing to suppress artifacts. PG-DL visibly outperforms all conventional methods in terms of artifact reduction. Blur metrics reported in the figures also align with these visual assessments.DISCUSSION and CONCLUSION
In this study, we enabled PG-DL reconstruction for 3D high-resolution non-Cartesian datasets, and investigated its performance on SIMBA acquisitions. The PG-DL reconstruction was trained on separate navigator-gated acquisitions, and generalized well to SIMBA clusters, visibly improving on conventional reconstructions. These preliminary results suggest that the motion extracted in the SIMBA clusters is consistent with navigator-gated acquisitions, but SIMBA acquisition is continuous and doesn’t require any planning. Furthermore, PG-DL can recover the image quality lost to the inherent undersampling in these clusters. Further benefits may be possible by reducing the SIMBA cluster sizes to reduce motion artifacts, and use PG-DL to reconstruct these highly-undersampled datasets, which warrants further investigation.Acknowledgements
This work was partially supported by NIH R01HL153146, NIH P41EB027061, NIH R21EB028369, NSF CAREER CCF-1651825.References
[1] J. Heerfordt et al., “Similarity‐driven multi‐dimensional binning algorithm (SIMBA) for free‐running motion‐suppressed whole‐heart MRA”. Magn Reson Med 2021;86:213–229.
[2] K. Hammernik, et al., “Learning a variational network for reconstruction of accelerated MRI data,” Magn Reson Med 2019:79:3055–3071.
[3] H. K. Aggarwal et al., “MoDL:Model-based deep learning architecture for inverseproblems,” IEEE Trans Med Imag 2019: 38(2):394–405.
[4] F. Knoll et al., “Deep-learning methodsfor parallel magnetic resonance imaging reconstruction: a survey of the current approaches, trends, and issues,” IEEE Sig Proc Mag 2020:37:128–140.
[5] M. O. Malave, et al., “Reconstructionof undersampled 3D non-Cartesian image-based naviga-tors for coronary MRA using an unrolled deep learningmodel,” Magn Reson Med, 2020:84:800–812.
[6] Z. Ramzi, et al., “Density compen-sated unrolled networks for non-cartesian MRI recon-struction,” in Proc IEEE ISBI 2021:1443–1447.
[7] M. Kellman, et al., “Memory-efficient learn-ing for large-scale computational imaging,” IEEE Trans Comp Imag 2020:6:1403–1414, 2020.
[8] C. A. Baron, et al, “Rapid compressed sensing reconstruction of 3D non-Cartesian MRI,” Magn Reson Med 2018:79(5):2685–2692.
[9] S. Micikevicius, et al., “Mixed precision training,” arXiv preprint arXiv:1710.03740
[10] D. Piccini et al., “Spiral phyllotaxis: the natural way to constructa 3D radial trajectory in MRI,” Magn Reson Med 2011:66(4):1049–1056.
[11] B. Yaman et al., Self-supervised learning of physics-guided reconstruction neural net-works without fully sampled reference data,” Magn Reson Med 2020:84(6):3172–3191.
[12] S. Coppo et al., “Free-Running 4D Whole-Heart Self-Navigated Golden Angle MRI: Initial Results”, Magn Reson Med 2015:74:1306–1316.
[13] F. Crete et al., ”The blur effect: perception and estimation with a new no-reference perceptual blur metric,” HVEI 2007:6492:64920I
Figures