4810

Zero-Shot Physics-Guided Self-Supervised Learning for  Subject-Specific MRI Reconstruction 
Burhaneddin Yaman1,2, Seyed Amir Hossein Hosseini1,2, and Mehmet Akcakaya1,2
1Electrical and Computer Engineering, University of Minnesota, Minneapolis, MN, United States, 2Center for Magnetic Resonance Research, Minneapolis, MN, United States

Synopsis

While self-supervised learning enables training of deep learning reconstruction without fully-sampled data, it still requires a database. Moreover, performance of pretrained models may degrade when applied to out-of-distribution data. We propose a zero-shot subject-specific self-supervised learning via data undersampling (ZS-SSDU) method, where acquired data from a single scan is split into at least three disjoint sets, which are respectively used only in physics-guided neural network, to define training loss, and to establish an early stopping strategy to avoid overfitting. Results on knee and brain MRI show that ZS-SSDU achieves improved artifact-free reconstruction, while tackling generalization issues of trained database models.

INTRODUCTION

Physics-guided deep learning (PG-DL) approaches have gained interest due to their improved reconstruction quality1-8. These methods use algorithm unrolling1-4, and are trained in a supervised manner. Self-supervised learning via data undersampling (SSDU)9,10 enables training PG-DL networks without fully-sampled data by retrospectively splitting available k-space measurements into two sets where one is used for data consistency (DC) in the unrolled network, while the other is used to define loss. While SSDU tackles the requirement of fully-sampled data, it still utilizes a database. However, in some MRI applications, such as those involving time-varying physiological processes, which may differ substantially between subjects, it may be difficult to generate high-quality databases of sufficient size. Moreover, recent works show that pretrained models may not generalize well when training and test datasets mismatch on image contrast, sampling pattern, SNR, vendor, or anatomy11. In this work, we propose zero-shot SSDU (ZS-SSDU), which enables subject-specific training of PG-DL networks. In cases, where a pretrained model exists, we further combine ZS-SSDU with transfer learning to achieve reduced computational complexity. We apply ZS-SSDU on fastMRI knee and brain MRI datasets, showing its efficacy over database-trained models.

THEORY

The inverse problem for MRI reconstruction is given as
$$\arg\min_{\bf x}\|\mathbf{y}_{\Omega}-\mathbf{E}_{\Omega}\mathbf{x}\|^2_2+\cal{R}(\mathbf{x}), (1)$$
where x is the image of interest, $$$\bf{y}_{\Omega}$$$ is acquired k-space with sub-sampling pattern Ω, $$$\bf{E}_{\Omega}$$$ is the multi-coil encoding operator. The first term in Eq. 1 enforces DC and $$$ \cal{R}(.)$$$ is a regularizer. In presence of fully-sampled data, supervised PG-DL is trained end-to-end via9
$$ \min_{\bf\theta} \frac1N\sum_{i=1}^{N}\mathcal{L}({\bf y}_{\textrm{ref}}^i,\:{\bf E}_\textrm{full}^if({\bf y}_{\Omega}^i,{\bf E}_{\Omega}^i;{\bf \theta})),(2)$$
where N is number of datasets in the database, $$${\bf y}_{\textrm{ref}}^i$$$ is fully-sampled k-space of ith subject, $$$f({\bf y}_{\Omega}^i,{\bf E}_{\Omega}^i; {\bf\theta})$$$ denotes network output with parameters θ, $$${\bf E}_\textrm{full}^i$$$ is fully-sampled encoding operator, and $$$\mathcal{L}(\cdot, \cdot)$$$ is training loss.
In absence of fully-sampled data, SSDU enables training by splitting acquired data locations Ω into two disjoint sets, Θ and Λ as Ω=ΘUΛ, where Θ and Λ denote the k-space locations used in DC units and loss function, respectively. SSDU is trained using9

$$\min_{\bf\theta}\frac1N\sum_{i=1}^{N}\mathcal{L}\Big({\bf y}_{\Lambda}^i,\: {\bf E}_{\Lambda}^i \big(f({\bf y}_{\Theta}^i,{\bf E}_{\Theta}^i;{\bf \theta})\big)\Big). (3)$$
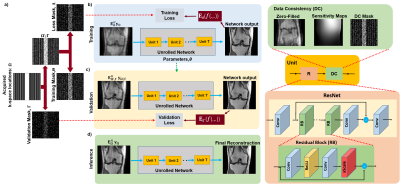
In the proposed, database-free ZS-SSDU (Fig. 1), acquired k-space locations from a single scan Ω is partitioned into disjoint sets as
$$\Omega=\Theta\sqcup\Lambda\sqcup\Gamma, (4)$$
where Θ and Λ are respectively used in DC units and to define loss for self-supervision. The third partition Γ is set aside for defining a k-space validation loss. Hence, ZS-SSDU training is both self-supervised and self-validated. To improve performance in this subject-specific setting, we generate multiple (Θ,Λ) pairs by fixing the k-space validation partition Γ⊂Ω, and retrospectively masking Ω\Γ multiple times. Formally, Ω\Γ is partitioned K times such that Ω\Γ=ΘkUΛk. We note that Λk,Θk and Γ are pairwise disjoint ∀ k. Proposed ZS-SSDU is thus trained using
$$\min_{\bf \theta}\frac{1}{K}\sum_{k=1}^{K} \mathcal{L}\Big({\bf y}_{\Lambda_k},\: {\bf E}_{\Lambda_k} \big(f({\bf y}_{\Theta_k},{\bf E}_{\Theta_k};{\bf\theta})\big)\Big), (5)$$
along with a k-space self-validation loss, which tests the generalization performance of the trained network on the validation partition Γ. For the $$$\ell^{th}$$$ epoch, where the learned network weights are specified by $$$\theta^{(l)}$$$, this validation loss is given by:
$$\mathcal{L}\Big({\bf y}_{\Gamma},\: {\bf E}_{\Gamma}\big(f({\bf y}_{\Omega\backslash\Gamma},{\bf E}_{\Omega\backslash\Gamma};{\bf\theta}^{(l)})\big)\Big).$$

METHODS

Experiments were performed on the multi-coil knee and brain data from fastMRI database12. Fully-sampled datasets were retrospectively undersampled by keeping 24 ACS lines from central k-space.

All PG-DL approaches were trained using Adam optimizer, learning rate=5×10-4, 100 epochs, and mixed normalized $$$\ell_1$$$-$$$\ell_2$$$ loss9. For all PG-DL approaches, a ResNet9 and conjugate-gradient2 were employed for regularizer and DC, respectively. Further comparisons were made with CG-SENSE, and deep-image-prior type reconstruction (DIP-Recon) that uses all acquired measurements Ω, for training and loss. Results were quantitatively evaluated using SSIM and PSNR. The k-space self-validation set Γ was selected from Ω using a uniformly random selection with |Γ|/|Ω|=0.2. The remaining indices Ω\Γ were retrospectively partitioned into disjoint 2-tuples multiple times based on uniformly random selection with the ratio ρ=|Λ|/|Ω\Γ|=0.4 ∀ k∈{1, . . . , K}.

RESULTS

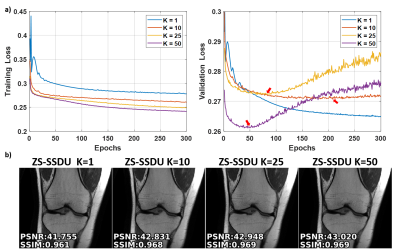
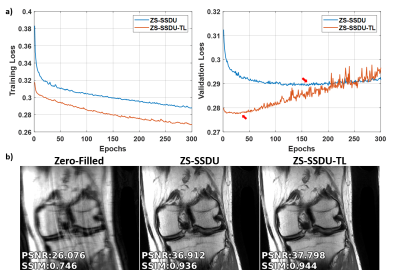
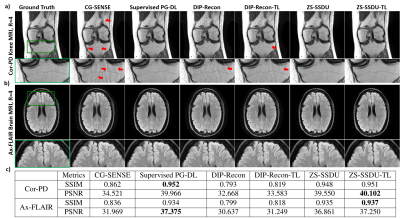
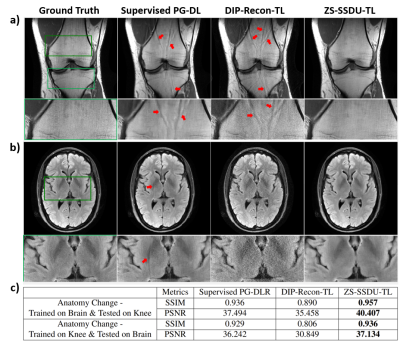
Fig. 2a shows representative subject-specific training and validation loss curves at R=4 of ZS-SSDU for K∈{1,10,25,50}. Validation loss for K=1 decreases without a clear breaking point for stopping. For K>1, validation loss forms an L-curve, and the breaking point of the L-curve is used as the stopping criterion. Fig. 2b show reconstructions corresponding to each K value. K=10 is used in the remainder of study. Fig. 3 shows loss curves and reconstruction results on a representative slice with and without transfer learning. As expected, ZS-SSDU-TL converges faster compared to ZS-SSDU. Fig. 4 shows reconstruction results and average quantitative metrics at R=4 for Cor-PD knee and Ax-FLAIR brain MRI datasets, when testing and training settings are matched. ZS-SSDU achieves artifact-free reconstruction, similar to supervised PG-DL. Fig. 5 shows reconstruction results and average metrics when the anatomy changes between training and test data. ZS-SSDU achieves artifact-free reconstruction, while supervised PG-DL and DIP-Recon suffer from artifacts.

DISCUSSION and CONCLUSIONS

In this study, we proposed zero-shot SSDU that enables subject-specific training of PG-DL networks with a well-defined stopping criterion. Results on knee and brain MRI showed that ZS-SSDU achieves artifact-free performance on-par with supervised PG-DL, when training and test data were from same distribution, while outperforming it if there was mismatch between training and test data characteristics.

Acknowledgements

Grant support: NIH R01HL153146, NIH P41EB027061, NIH U01EB025144; NSF CAREER CCF-1651825

References

1. Hammernik K, Klatzer T, Kobler E, Recht MP, Sodickson DK, Pock T, Knoll F. Learning a variational network for reconstruction of accelerated MRI data. Magn Reson Med 2018;79(6):3055-3071.

2. Aggarwal HK, Mani MP, Jacob M. MoDL: Model-Based Deep Learning Architecture for Inverse Problems. IEEE Trans Med Imaging 2019;38(2):394-405.

3. Hosseini SAH, Yaman B, Moeller S, Hong M, Akcakaya M. Dense Recurrent Neural Networks for Inverse Problems: History-Cognizant Unrolling of Optimization Algorithms. IEEE Journal of Selected Topics in Signal Processing 2020;14(6):1280-1291.

4. Liang D, Cheng J, Ke Z, Ying L. Deep Magnetic Resonance Image Reconstruction: Inverse Problems Meet Neural Networks. IEEE Signal Processing Magazine; 2020. p 141-151.

5. Schlemper J, Caballero J, Hajnal JV, Price AN, Rueckert D. A Deep Cascade of Convolutional Neural Networks for Dynamic MR Image Reconstruction. IEEE Trans Med Imaging 2018;37(2):491-503.

6. Qin C, Schlemper J, Caballero J, Price AN, Hajnal JV, Rueckert D. Convolutional Recurrent Neural Networks for Dynamic MR Image Reconstruction. IEEE Trans Med Imaging 2019;38(1):280-290.

7. Tamir JI, Yu SX, Lustig M. Unsupervised Deep Basis Pursuit: Learning inverse problems without ground-truth data. Advances in Neural Information Processing Systems Workshops; 2019.

8. Kellman M, Zhang K, Tamir J, Bostan E, Lustig M, Waller L. Memory-efficient Learning for Large-scale Computational Imaging. arXiv:2003.05551; 2020.

9. Yaman B, Hosseini SAH, Moeller S, Ellermann J, Uğurbil K, Akçakaya M. Self-supervised learning of physics-guided reconstruction neural networks without fully sampled reference data. Magn Reson Med 2020;84(6):3172-3191.

10. Yaman B, Hosseini SAH, Moeller S, Ellermann J, Ugurbil K, Akcakaya M. Self-Supervised Physics-Based Deep Learning MRI Reconstruction Without Fully-Sampled Data. IEEE 17th International Symposium on Biomedical Imaging (ISBI); 2020. p 921-925.

11. Muckley MJ, Riemenschneider B, Radmanesh A, Kim S, Jeong G, Ko J,Jun Y,Shin H, Hwang D, Mostapha M, Arberet S, Nickel D, Ramzi Z, Ciuciu P, Starck LJ, Teuwen J, Karkalousos D, Zhang C, Sriram A, Huang Z, Yakubova N, Lui Y, Knoll F. State-of-the-art Machine Learning MRI Reconstruction in 2020: Results of the Second fastMRI Challenge. IEEE Trans Med Imaging 2021;40(9):2306-2317.

12. Knoll F, Zbontar J, Sriram A, Muckley MJ, Bruno M, Defazio A, Parente M, Geras KJ, Katsnelson J, Chandarana H, Zhang Z, Drozdzalv M, Romero A, Rabbat M, Vincent P, Pinkerton J, Wang D, Yakubova N, Owens E, Zitnick CL, Recht MP, Sodickson DK, Lui YW. fastMRI: A Publicly Available Raw k-Space and DICOM Dataset of Knee Images for Accelerated MR Image Reconstruction Using Machine Learning. Radiol Artif Intell 2020;2(1):e190007.

Figures

Figure 1. a) Acquired measurements for a single scan are split into three sets: a training (Θ) and loss mask (Λ) for self-supervision, and validation mask (Γ) for early stopping. b) The parameters, θ, of the network are updated using Θ and Λ in data consistency (DC) units of network and for defining loss, respectively. c) Concurrently, a k-space validation procedure is used to establish stopping criterion by using Ω\Γ in DC units and Γ to measure a validation loss. d) Final reconstruction is performed using relevant learned parameters and all the acquired measurements in the DC unit.

Figure 2. a) Representative training and validation losses for ZS-SSDU with multiple K ∈ {1, 10, 25, 50} masks on a coronal PD knee dataset using uniform undersampling at R=4. For K > 1 the validation loss forms an L-curve, whose breaking point (red arrows) dictates the early stopping criterion for training. b) Corresponding ZS-SSDU reconstruction results. At K = 1, without a clear stopping criterion, visible artifacts remain, highlighting the overfitting. For K > 1, ZS-SSDU shows good reconstruction quality without residual artifacts. K=10 is used for remainder of the study.

Figure 3. a) Loss curves ZS-SSDU with/without transfer learning (TL) from a database-pretrained model for K = 10 on a representative coronal PD knee slice. ZS-SSDU with TL converges faster compared to ZS-SSDU (red arrows), owing to its better starting point. b) Reconstruction results corresponding to the loss curves. Both ZS-SSDU and ZS-SSDU-TL removes residual artifacts successfully.

Figure 4. Reconstruction results on a representative test slice from a) Cor-PD knee MRI and b) Ax-FLAIR brain MRI at R=4 with uniform undersampling. CG-SENSE, DIP-Recon, DIP-Recon-TL suffer from noise amplification and residual artifacts shown with red arrows, especially in knee MRI due to the unfavorable coil geometry. Scan-specific ZS-SSDU and ZS-SSDU-TL achieve artifact-free and improved reconstruction quality, similar to the database-trained supervised PG-DL. c) Average PSNR and SSIM values on 30 test slices.

Figure 5. Using pre-trained a) Ax-FLAIR and b) Cor-PD models for Cor-PD and Ax-FLAIR reconstructions, respectively. When used across different anatomies, supervised PG-DL reconstruction exhibits artifacts (red arrows). DIP-Recon-TL also has artifacts, while ZS-SSDU-TL achieves artifact-free reconstruction in both cases. Note ZS-SSDU without TL is not shown, since it does not have a similar generalizability issue compared to supervised PG-DL or TL approaches. c) Average PSNR and SSIM values on 30 test slices.

Proc. Intl. Soc. Mag. Reson. Med. 30 (2022)
4810
DOI: https://doi.org/10.58530/2022/4810