Introduction

Advanced reconstruction methods have become more widely adopted to address the SNR challenge in MRSI¹. Neural network (NN) derived priors have shown potential in achieving higher-quality MRSI reconstructions^2-9. One approach to leverage NN is to train end-to-end networks that directly map noisy, artifact-corrupted data to high-SNR, artifact-free data^2-4. An alternative approach is to formulate an optimization problem that integrates the physical forward model and network prior^5-9. While the second approach can be flexibly adapted for different acquisition parameters and SNRs, it often solves a high-dimensional, nonconvex problem that requires backpropagation and calculation of large Jacobian matrices, which is computationally demanding. Here, we propose a new method for MRSI reconstruction, called RAIISE (joint leaRning of nonlineAr representatIon and projectIon for faSt constrained MRSI rEconstruction). RAIISE is characterized by three key features: (a) a novel strategy to jointly learn low-dimensional representations of high-dimensional spectroscopic signals and a network-based projector that recover the low-dimensional embeddings from noisy data; (b) a formulation that integrates the encoding model, a nonlinear low-dimensional model constraint enforced through the learned projector, and complementary spatial constraint(s); and (c) a highly efficient algorithm based on alternating-direction-method-of-multipliers (ADMM) and NN-based projected gradient descent (PGD)^10,11. We have evaluated RAIISE using simulations as well as in vivo ³¹P-MRSI and ¹H-MRSI data. Impressive SNR-enhancement is demonstrated, both qualitatively and quantitatively. Key details for RAIISE are provided below.

Theory and Methods

Learning nonlinear representation and projection for MRSI

Learned nonlinear representations can be effective constraints for improved reconstruction from noisy MRSI data. As already described previously^7-9, the representations can be learned using deep-autoencoder-based networks (Fig. 1 top section). Let $$$E(.;\boldsymbol{\theta}_e)$$$ and $$$D(.;\boldsymbol{\theta}_d)$$$ denote the learned encoder and decoder (either fully connected^7,8 or containing convolutional layers⁹) with $$$\boldsymbol{\theta}_e$$$ and $$$\boldsymbol{\theta}_d$$$ representing the corresponding parameters, enforcing this low-dimensional representation for the desired true signals during reconstruction (i.e., $$$\|D(E(x;\boldsymbol{\theta}_e);\boldsymbol{\theta}_d)-x\|_2^2$$$) can be computationally challenging. RAIISE seeks to learn a projection network to address this issue. Specifically, we generated different noisy samples $$$\left\{{\widetilde{x}}_i\right\}$$$ at various SNRs, i.e., $$$\tilde{x}_i=x_i+e_i$$$ (Fig. 1, bottom section), and trained a projector to recover the low-dimensional embeddings as follows:
$${\hat{\boldsymbol{\theta}}}_p=\arg{\min_{\boldsymbol{\theta}_p}{\frac{1}{M}\sum_{m=1}^{M}{\epsilon_1\left(E\left(x_m;\boldsymbol{\theta}_e\right),P\left({\widetilde{x}}_m;\boldsymbol{\theta}_p\right)\right)+\lambda\epsilon_2(x_m,D(P\left({\widetilde{x}}_m;\boldsymbol{\theta}_p\right);\boldsymbol{\theta}_d))}}},\ \ (1)$$
where $$$P(.;\boldsymbol{\theta}_p)$$$ denotes the projector with parameters $$$\boldsymbol{\theta}_p$$$ (input being noisy data), $$$\epsilon_1$$$ and $$$\epsilon_2$$$ assess the “projection” errors for the low-dimensional features and the full signals, respectively, and $$$\lambda$$$ balances the two losses. The encoder $$$E(.)$$$ and decoder $$$D(.)$$$ are from the representation network. Note that the projector can be trained with different structures adapted to the data characteristics (single or multi-TE FIDs), and $$$\epsilon_1$$$ and $$$\epsilon_2$$$ can be chosen separately. In this study, the projector had the same architecture as the encoder, and mean-squared-error (MSE) was used.

Reconstruction using the learned projector

With the learned projector, RAIISE formulates the reconstruction problem as follows
$$\hat{\mathbf{X}}=\arg{\min_{\mathbf{X}\in D\left(\mathbf{z}\right)}{||\mathbf{d}-\mathcal{F}_\Omega\left\{\mathbf{B}\odot\mathbf{X}\right\}||_2^2}}+\gamma\ R\left(\mathbf{X}\right),\ \ (2)$$
where $$$\mathbf{X}\in D\left(\mathbf{z}\right)$$$ ($$$D$$$ the decoder) enforces the prior that the underlying true spectroscopic signal $$$\mathbf{X}$$$ should yield a low-dimensional representation (residing on a low-dimensional manifold). $$$\mathbf{B}$$$ models the B₀ inhomogeneity, $$$\mathcal{F}_\Omega$$$ an encoding operator with sampling pattern $$$\Omega$$$, $$$\mathbf{d}$$$ the noisy (k, t)-space measurements, and $$$R(.)$$$ impose a complementary constraint with parameter $$$\gamma$$$, e.g., $$$R\left(\mathbf{X}\right)=\|\mathbf{D}_w\mathbf{X}\|_1$$$ in this work, where $$$\mathbf{D}_w$$$ is a weighted finite-difference operator.
A variable-splitting ADMM-based method was used to handle the nonquadratic $$$R\left(\mathbf{X}\right)$$$ i.e., with $$$\mathbf{D}_w\mathbf{X}=\mathbf{S}$$$, the algorithm alternates between the following subproblems:
$$\mathbf{S}^{t+1}=\arg\min_{\mathbf{S}}\lambda\|\mathbf{S}\|_1+\frac{\mu}{2}\|\mathbf{D}_w\mathbf{X}^t-\mathbf{S}+\frac{\mathbf{Y}^t}{\mu}\|^2_F,\ \ (3)$$ $$\mathbf{X}^{t+1}=\arg\min_{\mathbf{X}\in D(\mathbf{z})}\|\mathbf{d}-\mathcal{F}_\Omega\{\mathbf{B}\odot\mathbf{X}\}\|_2^2+\frac{\mu}{2}\|\mathbf{D}_w\mathbf{X}\mathbf{S}^{t+1}+\frac{\mathbf{Y}^t}{\mu}\|^2_F,\ \ (4)$$
and updating the Lagrangian multiplier $$$\mathbf{Y}$$$. The subproblem in (3) can be solved by soft-thresholding, while the subproblem in (4) can be efficiently solved by a fast PGD algorithm^10,11. The projector during PGD was $$$\text{Proj}(.):=D(P(.;\hat{\boldsymbol{\theta}}_p),\boldsymbol{\theta}_d)$$$. The remaining algorithmic and theoretical details were omitted.

Results

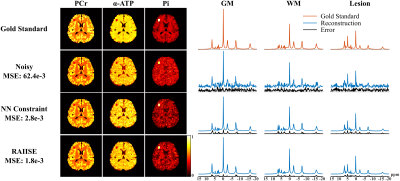
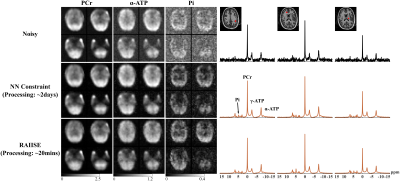
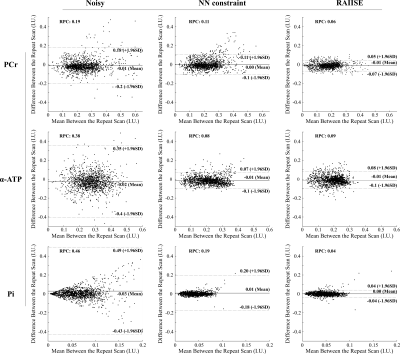
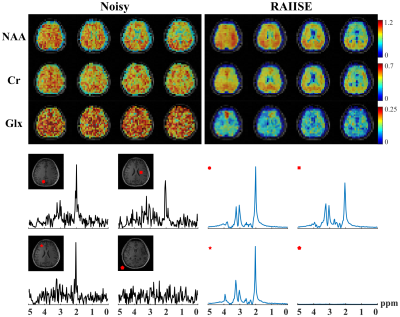
Figure 2 shows reconstructions from a numerical ³¹P-MRSI phantom (see [7] for details). We also compared RAIISE with the reconstruction from a previously reported NN-based method that achieved state-of-the-art performance (referred to as the NN constraint), for both simulation and in vivo data⁷. Significant SNR improvement and higher reconstruction accuracy were achieved by both methods compared to noisy data, while RAIISE produced slightly better accuracy, according to the MSE, metabolite maps, and localized spectra. More importantly, RAIISE is dramatically faster than the previous method (~5 mins vs. ~4.5 hrs). A set of reconstructions from in vivo ³¹P-MRSI data are shown in Fig. 3 (acquisition parameters: TR/TE = 250/1.3 ms, FOV = 180*200*180 mm³, matrix size = 28*30*13, spectral bandwidth = 5000 Hz and 512 FID points)¹². As can be seen, both methods yielded significant SNR enhancement over the noisy data, especially for low-abundance metabolites, while RAIISE is much faster (~20 mins vs. ~2 days; ~100X acceleration). For a further quantitative evaluation, a test-retest experiment was conducted, and Fig. 4 shows a Bland-Altman analysis of metabolite quantification results. The improved reproducibility and consistency between measurements can be clearly seen for the proposed method. To demonstrate the wide applicability of RAIISE, we also performed training and reconstruction using ¹H-MRSI data. SNR improvements for both metabolite maps (revealing contrasts concealed by noise) and voxel spectra can be observed for in vivo data (Fig. 5; acquisition parameters in figure caption). All studies received IRB approval.

Conclusion

RAIISE achieved highly computationally efficient SNR-enhancing MRSI reconstruction using NN-based priors, and has shown great potential for various high-dimensional MRSI acquisitions.

Acknowledgements

This work was supported in part by NSF-CBET-1944249 and NIH-NIBIB-1R21EB029076A.

References

[1] Maudsley AA, et al. Advanced magnetic resonance spectroscopic neuroimaging: Experts' consensus recommendations. NMR Biomed, 2021;34:e4309.

[2] Koonjoo N, et al. In vivo Cerebellum MRSI reconstruction by domain-transform manifold learning. In Proc of ISMRM, 2021;p. 2022.

[3] Lee HH, et al. Intact metabolite spectrum mining by deep learning in proton magnetic resonance spectroscopy of the brain. MRM, 2019;82:33-48.

[4] Qu X, et al. Accelerated nuclear magnetic resonance spectroscopy with deep learning. Angew Chem, 2020;132:10383-6.

[5] Li Y, et al. Machine learning-enabled high-resolution dynamic deuterium MR spectroscopic imaging. IEEE-TMI, 2021, In Press.

[6] Gong K, et al. High resolution MR spectroscopic imaging using deep image prior constrained subspace modeling. In Proc of ISMRM, 2020;p. 388.

[7] Lam F, et al. Constrained magnetic resonance spectroscopic imaging by learning nonlinear low-dimensional models. IEEE-TMI, 2020;39:545-555.

[8] Li Y, et al. Separation of metabolites and macromolecules for short-TE ¹H-MRSI using learned component-specific representations. IEEE-TMI, 2021;40:1157-1167.

[9] Li Y, et al. SNR-enhancing reconstruction for multi-TE MRSI using a learned nonlinear low-dimensional model. In Proc of ISMRM, 2021;p. 1998.

[10] Raj A, et al. GAN-based projector for faster recovery with convergence guarantees in linear inverse problems. In Proc of ICCV, 2019;pp. 5602-5611.

[11] Gupta H, et al. CNN-based projected gradient descent for consistent CT image reconstruction. IEEE-TMI, 2018;37:1440-1453.

[12] Ruhm L, et al. 3D ³¹P MRSI of the human brain at 9.4 Tesla: optimization and quantitative analysis of metabolic images. MRM, 2021;86:2368-2383.

[13] Ratiney H, et al. Time-domain quantitation of 1H short echo-time signals: background accommodation. Magn Reson Mater Phys Biol Med, 2004;16:284–296.