Introduction

The quality of 3D reconstruction of fetal MRI from multiple stacks of slices is highly dependent on the initialization of slice-to-volume transformations [1]. Fetal motion in clinical imaging further complicates the volume reconstruction process. Previous methods [1,2] addressed this problem by predicting the rigid transformation of each slice with deep neural networks. However, by processing each slice independently, this approach ignores the correlation between data in different (not necessarily neighboring) slices in one scan. Here we propose the Slice-to-Volume Registration Transformer (SVoRT), which considers multiple stacks of slices acquired in one scan as a sequence of images and predicts rigid transformations of all the slices simultaneously by sharing information across the slices.

Methods

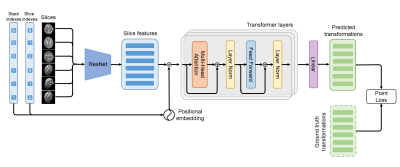
The architecture of SVoRT is shown in Fig. 1. SVoRT considers multiple stacks of slices as a sequence. Each slice in the sequence is associated with two indices, the index of the stack that the slice belongs to and the index of the slice in the stack. A ResNet [3] is used to extract features from slices and positional embeddings [4] are generated from the stack and slice indexes. The features and the corresponding positional embeddings are added and provided to a transformer network [4] with 3 transformer layers. Each transformer layer consists of a multi-head attention module, a feed forward network, and two layer normalizations [5]. Let $$$X$$$ be the $$$n\times~d$$$ input feature matrix, where $$$n$$$ is the number of slices and $$$d$$$ is the number of features. The multi-head attention module first projects $$$X$$$ into three different spaces,
$$Q_i=XW_i^Q,~K_i=XW_i^K,~V_i=XW_i^V,~i=1,\dots,h$$
where $$$W_i^Q$$$, $$$W_i^K$$$, and $$$W_i^V$$$ are $$$d\times(d/h)$$$ weight matrices, $$$i$$$ and $$$h$$$ are the index of head and total number of heads respectively. Then, each head computes the output as
$$Y_i=\text{softmax}\left(\frac{Q_iK_i^T}{\sqrt{d}}\right)V_i,~i=1,\dots,h,$$
where the softmax function is applied to each row. Finally, the outputs from all heads are aggregated and projected with a $$$d\times~d$$$ matrix, $$$W^O$$$,
$$Y=\text{concat}(Y_1,\dots,Y_h)W^O.$$
The feed forward network is a linear network applied on the features of each slice to extract deeper features. At the end, a linear layer is used to regress rigid transformation parameters from the output of the transformer.
We train the network with the point loss [1],
$$L=||\hat{P}_1-P_1||_2^2+||\hat{P}_2-P_2||_2^2+||\hat{P}_3-P_3||_2^2,$$
where $$$\hat{P}_1,~\hat{P}_2,~\hat{P}_3$$$ are the 3d locations of three different points (center, bottom left and bottom right) in the slice after the predicted transformation, and $$$P_1,~P_2,~P_3$$$ are the ground truth locations. In the experiments, SVRnet [1] was used as a baseline method, which employs a VGGNet [6] to predict the transformation of each slice independently.
We evaluate the models on the FeTA dataset [7], which consists of 80 T2-weighted fetal brain volumes with gestational age between 20 and 35 weeks. The dataset is split into training (68 subjects) and test (12 subjects) sets. We resampled the volumes to 0.8 mm isotropic, and simulated 2D slices with resolution of $$$1\text{mm}\times1\text{mm}$$$, slice thickness of $$$3\text{mm}$$$, matrix size of $$$128\times128$$$. Each training sample consisted of 3 stacks of slices and the orientation of each stack was randomly chosen. Fetal brain motion was simulated with trajectories similar to [8,9]. We also used various data augmentation techniques similar to [10], including image noise, bias field, signal void artifacts, and gamma transforms. During inference, we used the predicted transformations to initialize the 3D reconstruction algorithm [11]. The models were evaluated in terms of registration error and reconstruction quality.
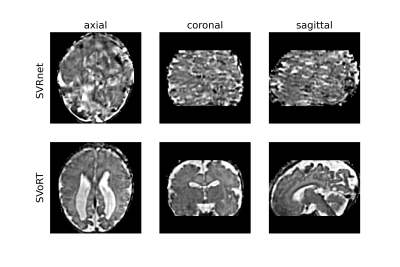
We also tested the trained model with data acquired in a real fetal MRI scan. Five stacks of 2D HASTE slices were acquired with resolution of $$$1\text{mm}\times1\text{mm}$$$, slice thickness of $$$3\text{mm}$$$, and matrix size of $$$256\times256$$$. Brain ROIs were manually segmented. Since there is no ground truth for this dataset, we only compared the perceptual quality of the reconstructed volumes.

Results and Discussion

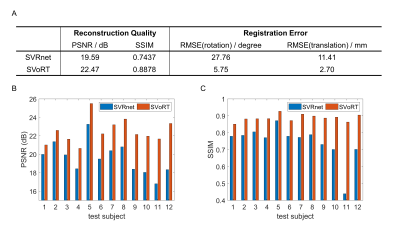
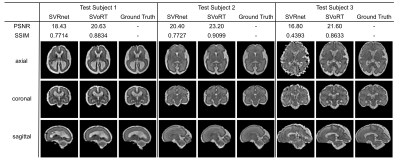
Fig. 2 reports the PSNR and SSIM of the reconstruction volumes and the registration errors. SVoRT outperforms SVRnet in terms of both reconstruction quality and registration accuracy. Since SVRnet registers each slice independently, slices with small brain ROI do not contain enough information, and may lead to large registration errors. In contrast, SVoRT leverages the relevance between slices detected by the self-attention mechanism when predicting the transformation. The reconstructed results in Fig. 3 show that SVoRT also has better perceptual quality due to fewer slice misalignments. From the reconstructed results of real data shown in Fig. 4, we observe that SVRnet fails to register the slices while SVoRT predicts the transformations correctly, indicating that SVoRT learns more robust features from massively augmented data, and therefore generalizes well in the presence of real-world noise and artifacts.

Conclusion

In this work, we propose a novel method for slice-to-volume registration in fetal brain MRI using transformers. By jointly processing the stacks of slices as a sequence, SVoRT registers each slice by utilizing context from other slices, resulting in lower registration error and better reconstruction quality. In addition, SVoRT learns more robust features so that, by training on simulated data, it generalizes well to data acquired in real scans. SVoRT provides a robust and accurate solution to the initialization of fetal brain reconstruction problem.

Acknowledgements

This research was supported by NIH U01HD087211, NIH R01EB01733, NIH HD100009, NIH NIBIB NAC P41EB015902, NIH 1R01AG070988-01, 1RF1MH123195-01 (BRAIN Initiative), ERC Starting Grant 677697, Alzheimer's Research UK ARUK-IRG2019A-003.