4804
Accelerated MR screenings with direct k-space classification1Courant Institute of Mathematical Sciences, New York University, New York, NY, United States, 2Center for Advanced Imaging Innovation and Research (CAI2R), Department of Radiology, New York University Grossman School of Medicine, New York, NY, United States, 3Department of Population Health, New York University, New York, NY, United States, 4Center for Data Science, New York University, New York, NY, United States
Synopsis
Despite its rich clinical information content, MR has seen limited adoption in population-level screenings, due to concerns about specificity combined with high scan duration and cost. In order to begin to address such issues, and to accelerate the entire pipeline from data acquisition to diagnosis, we introduce ARMS, an algorithm that learns k-space undersampling patterns to maximize the accuracy of pathology detection. ARMS detects pathologies directly from undersampled k-space data, bypassing explicit image reconstruction. We use ARMS to detect clinically significant prostate cancer and knee abnormalities in 2D MR scans, achieving an acceleration of 12.5x without compromising accuracy.
Introduction
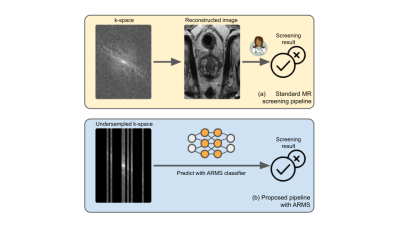
Despite its rich clinical information content, MR has seen limited adoption in population-level screenings, due to concerns about high scan duration and cost. Efforts to accelerate MR exams focus on reconstructing high-fidelity images using under-sampled k-space data [6, 7, 8, 21], however extensive k-space coverage is required to produce high-fidelity images for radiologists to accurately discern a pathology. The focus on producing high-fidelity images inherently limits the achievable acceleration.We propose AcceleRated Mr Screener (ARMS), a method that augments MR scanning with AI to significantly speed up the process from data acquisition to the final diagnostic assessment, with the aim of making population-level MR screening feasible in some settings. ARMS predicts the response variable directly from the learned undersampled k-space data, bypassing explicit image reconstruction. ARMS is not intended to replace comprehensive radiologic image interpretation, but rather to facilitate automated and accurate screening that could result in early warning and targeted referrals for further clinical follow-up. Experiments using prostate and knee MR scans demonstrate that ARMS achieves a 12.5x acceleration without any loss in performance compared to models trained on images reconstructed from fully-sampled k-space data.
Methods
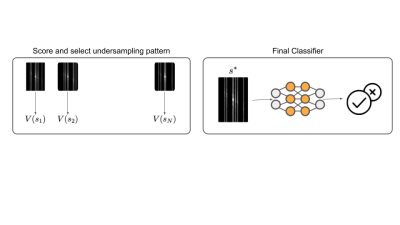
ARMS predicts the presence of a clinically relevant response variable $$$y$$$ directly from under-sampled k-space data that is optimized to contain a strong predictive signal for the response variable. The central idea behind ARMS is a method to estimate the predictive information content associated with any subset of k-space data.ARMS procedure. Given a user-defined acceleration factor, an undersampling pattern $$$s$$$ determines how to subsample the k-space data $$$x$$$. The undersampled k-space is referred to as $$$x_s$$$.
The first step of ARMS involves assigning a “value” to under-sampling patterns $$$s$$$. The value $$$v(s)$$$ corresponds to the mutual information between $$$x_s$$$ and $$$y: \mathbb{E}_x \mathbb{E}_{y|x}\log p(y|x_s)+C$$$, where $$$C$$$ is a constant. Estimating this mutual information for every $$$s$$$ requires learning $$$p(y|x_s)$$$ many times, which is infeasible. Instead, following [10,19] we estimate this mutual information by learning a single parametric function $$$v_\theta(s)$$$. The function $$$v_\theta(s)$$$ is the performance of a deep learning classifier that predicts $$$y$$$ from $$$x_s$$$. The classifier is trained by predicting $$$y$$$ from randomly masked k-space. This classifier is a convolutional neural network modified to use k-space inputs. We replace the first convolutional layer with an element-wise multiplication layer, since element-wise multiplication in the Fourier domain is equivalent to convolution in the spatial domain.
The second step of ARMS involves choosing an optimal undersampling pattern via Monte Carlo search. $$$N$$$ samples of $$$s$$$ are generated, using a one-dimensional variable density prior [8]. We select the undersampling pattern, $$$s*$$$, that maximizes the value function, estimated on a validation set. Finally, to predict pathologies, ARMS uses the classifier in $$$v_\theta$$$ with undersampled k-space $$$x_{s*}$$$.
Experiments and Results
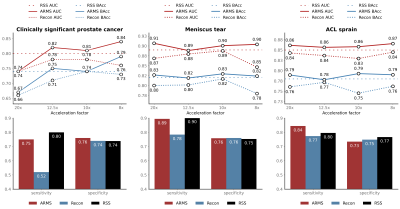
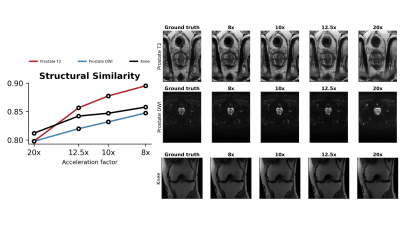
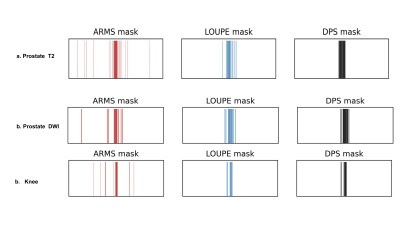
We evaluate ARMS on three different tasks: (a) detecting the presence of clinically significant prostate cancer in abdominal MR scans; (b) detecting the presence of meniscal tear in knee MR scans; and (c) detecting the presence of ACL sprain also in knee MR scans. We explore the performance of ARMS for a set of four different acceleration factors: $$$\{20,12.5,10,8\}$$$.We compare the ARMS classifier against several accelerated MR screening methods. These screening methods first reconstruct images from undersampled k-space data, then train classifiers to predict responses from the reconstructed images. We employ two reconstruction methods: U-Net [11] and VarNet [7]. We report reconstruction metrics in Figure 3 and compare reconstruction-optimized under-sampling patterns with ARMS patterns in Figure 4.
In addition, we compare ARMS against a classifier that uses the fully-sampled, RSS combined, ground truth images[13]. For both ARMS and image classifiers, we use the pre-activation ResNet [16] architecture.
Prostate data. For the prostate data, we use retrospectively collected scans performed clinically at NYU in 313 subjects referred for suspicion of prostate cancer on a 3T Siemens scanner with a 30-element body coil array. Examinations included a T2-weighted TSE sequence with scan time of 3.87 min (TR=4s,ETL=25,), and a diffusion-weighted EPI sequence (ETL=75, TR=5.8-6.5s) using b=50 and 1000 in three directions with scan time of 5.4 min. T2 and DWI axial abdominal MR scans were used to predict the presence of clinically significant prostate cancer in 2D slices with a lesion, identified by board-certified abdominal radiologist, labeled as clinically significant if its PI-RADS score $$$\geq$$$ 3 [17].The training, validation and test sets consist of 218, 48, and 47 volumes, respectively.
Knee data. We use the FastMRI dataset [6] with slice-level annotations from FastMRI+ [18], consisting of coronal proton density scans. Scan parameters are available in [6]. The training, validation, and test sets consist of 816, 176, and 175 volumes respectively. We predict the incidence of both meniscus tear and ACL sprain in a 2D slice.
Results. At 12.5x, ARMS suffers no drop in classification performance compared to the RSS baseline, while uniformly outperforming the reconstruction-based image classifiers for both knee and prostate tasks. We report the classification metrics of ARMS and the baselines in Figure 2.
Conclusion
ARMS demonstrates that direct k-space classification can provide significant speed-ups in MR screening times without any loss in predictive performance. Future work will explore active prospective sampling and screening performance using low-field MR scanners.Acknowledgements
Raghav Singhal and Mukund Sudarshan contributed equally. We would like to acknowledge Patricia M Johnson for her constant support. This work is supported by NIH grants P41 EB017183 and R21 CA256324. Rajesh Ranganath is partially supported by NSF Award 1922658 NRT-HDR: : FUTURE Foundations, Translation, and Responsibility for Data Science.References
[1] Susan Slatkoff, Stephen Gamboa, Adam J Zolotor, Anne L Mounsey, and Kohar Jones. PSA testing: When it’s useful, when it’s not.The Journal of family practice, 60(6):357, 2011.
[2] Dragan Ilic, Mia Djulbegovic, Jae Hung Jung, Eu Chang Hwang, Qi Zhou, Anne Cleves,Thomas Agoritsas, and Philipp Dahm. Prostate cancer screening with prostate-specific antigen(psa) test: a systematic review and meta-analysis.Bmj, 362, 2018
[3] Satoshi Washino, Tomohisa Okochi, Kimitoshi Saito, Tsuzumi Konishi, Masaru Hirai, YutakaKobayashi, and Tomoaki Miyagawa. Combination of prostate imaging reporting and data system (pi-rads) score and prostate-specific antigen (psa) density predicts biopsy outcome in prostate biopsy naïve patients. BJU international, 119(2):225–233, 2017.
[4] J Elvenes, CP Jerome, O Reikerås, and O Johansen. Magnetic resonance imaging as a screening procedure to avoid arthroscopy for meniscal tears. Archives of orthopaedic and trauma surgery,120(1-2):14–16, 2000
[5] Maria Adele Marino, Thomas Helbich, Pascal Baltzer, and Katja Pinker-Domenig. Multipara-metric mri of the breast: A review.Journal of Magnetic Resonance Imaging, 47(2):301–315,2018.
[6] Zbontar, Jure, et al. "fastMRI: An open dataset and benchmarks for accelerated MRI." arXiv preprint arXiv:1811.08839 (2018).
[7] Sriram, Anuroop, et al. "End-to-end variational networks for accelerated MRI reconstruction." International Conference on Medical Image Computing and Computer-Assisted Intervention. Springer, Cham, 2020.
[8] Lustig, Michael, David Donoho, and John M. Pauly. "Sparse MRI: The application of compressed sensing for rapid MR imaging." Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine 58.6 (2007): 1182-1195.
[9] Muckley, Matthew J., et al. "State-of-the-art Machine Learning MRI reconstruction in 2020: Results of the second fastMRI challenge." arXiv preprint arXiv:2012.06318 (2020).
[10] Jethani, Neil, et al. "Have We Learned to Explain?: How Interpretability Methods Can Learn to Encode Predictions in their Interpretations." International Conference on Artificial Intelligence and Statistics. PMLR, 2021.
[11] Ronneberger, Olaf, Philipp Fischer, and Thomas Brox. "U-net: Convolutional networks for biomedical image segmentation." International Conference on Medical image computing and computer-assisted intervention. Springer, Cham, 2015.
[12] Muckley, Matthew J., et al. "Results of the 2020 fastmri challenge for machine learning mr image reconstruction." IEEE transactions on medical imaging 40.9 (2021): 2306-2317.
[13] Larsson, Erik G., et al. "SNR-optimality of sum-of-squares reconstruction for phased-array magnetic resonance imaging." Journal of Magnetic Resonance 163.1 (2003): 121-123.
[14] Bahadir, Cagla Deniz, Adrian V. Dalca, and Mert R. Sabuncu. "Learning-based optimization of the under-sampling pattern in MRI." International Conference on Information Processing in Medical Imaging. Springer, Cham, 2019.
[15] Huijben, Iris AM, Bastiaan S. Veeling, and Ruud JG van Sloun. "Learning sampling and model-based signal recovery for compressed sensing MRI." ICASSP 2020-2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). IEEE, 2020.
[16] He, Kaiming, et al. "Identity mappings in deep residual networks." European conference on computer vision. Springer, Cham, 2016
[17] Winkel, David J., et al. "A novel deep learning based computer-aided diagnosis system improves the accuracy and efficiency of radiologists in reading biparametric magnetic resonance images of the prostate: results of a multireader, multicase study." Investigative Radiology 56.10 (2021): 605-613.
[18] Zhao, Ruiyang, et al. "fastmri+: Clinical pathology annotations for knee and brain fully sampled multi-coil mri data." arXiv preprint arXiv:2109.03812 (2021).
[19] Jethani, Neil, et al. "FastSHAP: Real-Time Shapley Value Estimation." arXiv e-prints (2021): arXiv-2107.
[20] Covert, Ian, Scott Lundberg, and Su-In Lee. "Explaining by removing: A unified framework for model explanation." Journal of Machine Learning Research 22.209 (2021): 1-90.
[21] Hammernik, Kerstin, et al. "Learning a variational network for reconstruction of accelerated MRI data." Magnetic resonance in medicine 79.6 (2018): 3055-3071.
Figures