Introduction

Modern imaging techniques, and in particular functional magnetic resonance imaging (fMRI),¹ provide an opportunity to study brain organization and development noninvasively. The human brain is a highly interconnected network where local activation patterns are organized to cope with diverse environmental demands.² Recently, traditional graph structure has been used to construct brain functional connectome (functional connectivity network (FCN)), which might reveal the brain functional behavior through different activation patterns.³
Graph theory based method has been successfully applied to characterize brain FCNs with applications to prediction of mental health disorders and neurodevelopment outcomes.^4-7 More recently, hypergraph structure was utilized to construct the brain FCNs to incorporate the high-order relationships between individual regions.^8,9 In our recent work, a hypergraph learning framework has been proposed to improve the discriminative power of the constructed FCNs with weighted hyperedges.¹⁰ In this study, we incorporate the hypergraph structure to the conventional graph convolutional network (GCN) and propose a hypergraph learning based neural network (HGCN) to classify FCNs, which considers the higher order relationships in the network and the well-acknowledged performance of deep learning models for representation learning.

Methods

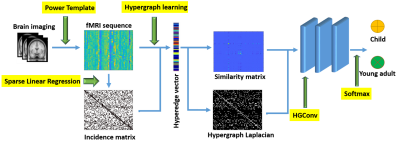
We begin by introducing basic notions in hypergraph theory. A hypergraph $$$\mathcal{G}=(\mathcal{V},\mathcal{E},\textbf{w})$$$ includes a vertex set $$$\mathcal{V}=\{v_1,v_2,\cdots,v_N\}$$$, a hyperedge set $$$\mathcal{E}=\{e_1,e_2,\cdots,e_M\}$$$ , and a hyperedge weight vector $$$\textbf{w}=(w(e_1),w(e_2),\cdots, w(e_M))^{T}\in\mathbb{R}^M$$$ . The hypergraph $$$\mathcal{G}$$$ can be denoted by an incidence matrix $$$\textbf{H}=[H_{ij}]\in \mathbb{R}^{N\times M}$$$ with entries
$$ H_{ij}={\begin{cases}1 & \text{if} \quad v_i\in e_j\\0 & \text{otherwise}.\\\end{cases} }$$
The vertex degree and hyperedge degree are defined as the weighted sum of the hyperedge that passes a given node and the sum of the vertices within a hyperedge, respectively, denoted in matrix form as $$$\textbf{D}_v$$$ and $$$\textbf{D}_e$$$. The similarity matrix of a hypergraph is defined by $$$\textbf{S}=\textbf{H}\textbf{W}\textbf{D}_e^{-1}\textbf{H}^{T}$$$ , where $$$\textbf{W}$$$ denotes the diagonal matrix of hyperedge weights.¹⁰ The hypergraph Laplacian matrix is defined by $$$\textbf{L}=\textbf{D}_v-\textbf{S}$$$.
In our proposed framework, the incidence matrix $$$\textbf{H}$$$ was constructed using the sparse linear regression $$\min_{{\alpha}_i}\;\frac{1}{2}\lVert\textbf{x}_i-\textbf{A}_i{\alpha}_i\rVert_{2}^{2}+\rho\lVert{\alpha}_i\rVert_1,$$ where $$$\textbf{A}_i=\left(\textbf{x}_1,\cdots,\textbf{x}_{i-1},\textbf{x}_{i+1},\cdots,\textbf{x}_N\right)$$$ is the time sequential data on all the vertices except the $$$i$$$-th one. $$${\alpha}_i$$$ reflects the neighborhood information towards centroid node $$$i$$$. $$$\rho$$$ is the regularization parameter controlling the sparsity. We then employ hypergraph learning to estimate hyperedge weights by minimizing the smoothness of the input data, which is quantified by the Laplacian quadratic form:
$$\begin{aligned}\min_{\textbf{w}} \; & \text{tr}(\textbf{X}^T\textbf{L}\textbf{X})+\delta\lVert\textbf{w}\rVert_{2}^{2}\\\textrm{s.t.} \; & \textbf{w}\succeq0\\ &\lVert\textbf{w}\rVert_{1}=1, \\\end{aligned}$$
where $$$\textbf{X}$$$ is the data matrix, and $$$\delta$$$ is a positive regulator controlling the hyperedge weight distribution. The two constraints enforce the learned weights are positive and non-trivial. Similar to the classical GCN,¹¹ we can perform hypergraph Fourier transform by replacing graph Laplacian matrix with the learned hypergraph Laplacian.¹² Approximated with the first order Chebyshev polynomial and using change of parameters, the hypergraph convolution layer is formulated:
$$ \textbf{X}^{(l+1)}=\sigma(\textbf{D}_v^{-\frac{1}{2}}\textbf{H}\textbf{W}\textbf{D}_e^{-1}\textbf{H}^{T}\textbf{D}_v^{-\frac{1}{2}}\textbf{X}^{(l)}\Theta^{(l)}),$$
where $$$ \textbf{X}^{(l)}$$$ is the input at $$$l$$$ -th layer $$$(\textbf{X}^{(0)}=\textbf{X})$$$, and $$$\sigma$$$ denotes the Rectified Linear Unit (ReLU) function.
We validated our proposed model on resting state fMRI data collected from the Philadelphia Neurodevelopmental Cohort (PNC), a large scale collaborative study between the Brain Behavior Laboratory at the University of Pennsylvania and the Center for Applied Genomics at the Children’s Hospital of Philadelphia.¹³ Subjects were scanned on a 3T Siemens Trio scanner with parameters: slice thickness = 3 mm, 64 slices, TR=3 s, TE=32 ms, flip angle=90◦ , matrix = 64×64, FOV=192 mm.
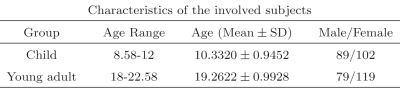
We followed a standard pipeline to preprocess the data using SPM12¹⁴, consisting of motion correction, spatial normalization to standard MNI space (adult template) and spatial smoothing with a 3 mm FWHM Gaussian kernel. We applied regression to remove the effect of motion (6 parameters), followed by a band-pass filter in 0.01Hz to 0.1Hz frequency range. The imaging data were further parcellated into 264 brain regions according to Power template.¹⁵ For classification, we divide the subjects in two groups as in Table 1.

Results

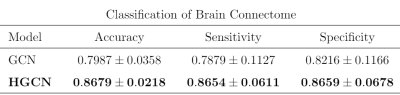
We built a three-layer HGCN to perform graph classification as in Figure 1. The model takes hypergraph similarity matrix as input and hypergraph Laplacian matrix to perform convolution. A k-nearest neighborhood (KNN) algorithm is enforced on the graph to control sparsity.¹⁶ The hyper-parameters including number of channels, learning rate, weight decay are tuned based on cross-entropy loss. A Softmax layer is used to output the label. For comparison, we also conducted the classification task with GCN¹¹, where the brain FCNs are constructed based on Pearson correlation.
Table 2 shows that the proposed HGCN outperforms conventional GCN model. Our model can classify subjects into the appropriate age groups using their FCNs with a mean balanced accuracy of 86.8%.

Discussion and conclusion

In this work, we developed a HGCN and applied it to a large neuroimaging dataset with resting state fMRI data. We demonstrated the superiority of our proposed method over conventional GCN by incorporating higher order relationships contained in the graph structure and the discriminative information from the hyperedge weights. We validated the effectiveness of our proposed method to predict a given subject’s age using resting state fMRI data. Our future directions include applying this method to meaningful clinical problems and to improve the accuracy of prognostic models for mental health and neurodevelopmental outcomes.

Acknowledgements

This work was supported by the National Institutes of Health [R01-EB029944, R01-EB030582, R01-NS094200 and R01-NS096037]. The funders played no role in the design, analysis, or presentation of the findings.