Introduction

Double-echo steady-state (DESS) sequences are a promising candidate for diffusion weighted imaging (DWI) free of geometric distortions¹. The design of diffusion-weighted DESS (dwDESS) sequences allows waveform variations for the diffusion weighting gradient G_D. While dwDESS sequences were originally introduced with unipolar G_D², also bipolar or higher order G_D are possible³. A balanced G_D (i.e., with nulling zeroth momentum) typically necessitates a spoiler gradient G_S to suppress banding artefacts⁴, which additionally increases the degrees of freedom in the design of dwDESS sequences.
This study explores different dwDESS sequence variants, with the following optimization criteria:
(a) the functional form of signal versus strength of G_D reflecting the ability to fit the Apparent Diffusion Coefficient (ADC) from the signal,
(b) the sensitivity of signal versus strength of G_D reflecting the reliability of the fitted ADC,
(c) the obtained signal strength reflecting the expected SNR of diffusion weighted images and fitted ADC map.

Methods

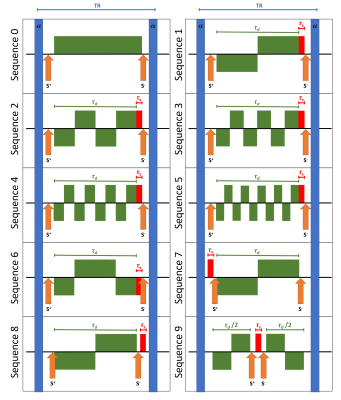
Different variants of dwDESS sequences were investigated in the framework of Extended Phase Graphs (EPG)⁵. All signals given below were calculated after applying 50 RF pulses to guarantee that steady state was reached in the sequence. The signals S- and S+ of the echoes directly before and after an RF pulse as well as their ratio ΔS = S-/S+ (corresponding to the diffusion weighted signal) were calculated.
Ten different sequence variants were investigated (Fig.1). Sequence 0 is the unipolar variant². In Sequences 1-5, G_D comprised n=1 to n=5 bipolar gradient pairs, each consisting of a negative and positive lobe of identical size. While Sequence 0 did not need an explicit G_S, G_S was added between the end of G_D and S- for Sequences 1-5^4,6. Sequence 6 differed from Sequence 2 (n=2) by inverting the polarization of the second gradient pair. Sequences 7/8 differed from Sequence 1 by shifting G_S before S+ / after S-. Sequence 9 differed from Sequence 6 by shifting G_S to TR/2 and the two bipolar G_D before S+ and after S-. All sequences shared the same TR=76 ms, same total length τ_D=74.1 ms of G_D, and same length τ_S=1.9 ms of G_S. (i.e., τ_S/τ_D=2.5%).
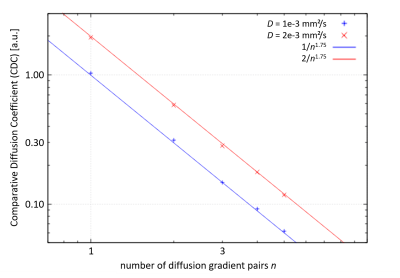
Each sequence simulation was repeated 7 times with p=40/50/…/90/100% of maximum gradient strength g_max=13 mT/m of G_D, yielding current gradient strength g=pg_max. The definition of an effective b-value (and thus, the determination of ADC) was possible if ΔS(g²) showed a mono-exponential shape (see above criterium (a))⁷. To investigate the sensitivity of ΔS versus g² (see criterium (b)), a “Comparative Diffusion Coefficient” (CDC) was defined via DS(g²) ~ exp(-CDC g²). The higher the obtained CDC, the higher the sensitivity of ΔS versus g², and thus the expected reliability of the ADC map. Sequence variants yielding no impact of g on ΔS (i.e. CDC=0) were excluded from this study beforehand.
Diffusivities D=1mm²/s and D=2mm²/s were applied throughout the study. Corresponding tests confirmed that T₁ and T₂ (within physiologic range) did not impact ΔS (as required for determination of ADC) but did impact S±. To enable comparison of S± from different sequence variants, T₁=350ms, T₂=250ms, and α=25° was assumed for all simulations in order to investigate criterium (c) defined above.

Results

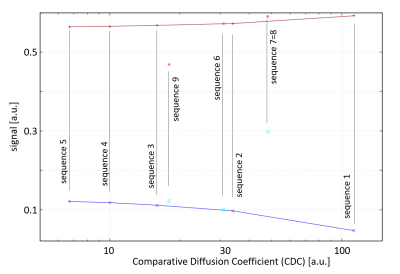
The desired mono-exponential behavior of ΔS(g²) was found for all investigated sequences except for Sequence 0, which was thus not further examined. For Sequences 1-5, a double logarithmic plot (Fig.2) of CDC versus n showed a functional behavior with CDC~n^-1.75, independent of D assumed in the simulation. CDC versus S± is shown for all sequences in Fig.3. Highest S± was found for Sequences 7/8, and highest CDC was found for Sequence 1.

Discussion

The following ranking of the investigated dwDESS sequence variants was obtained:
- Criterium (a) (mono-exponential behavior) is fulfilled by all sequence variants except Sequence 0 (unipolar G_D),
- Criterium (b) (reliability of fitting ADC, reflected by maximum CDC) is optimally fulfilled for Sequence 1 (bipolar G_D, G_S inside echoes),
- Criterium (c) (SNR of diffusion weighted images and ADC map, reflected by maximum S±) is optimally fulfilled for Sequences 7 and 8 (bipolar G_D, G_S outside echoes).
Thus, there is no dedicated, single sequence which optimally fulfills all criteria. Sequences with different n (Sequences 1-5) show a systematic trade-off between criteria (b) and (c). However, comparing Sequence 1 with Sequence 5, the gain in signal strength of S- is less than a factor of 3, while the loss in CDC is almost a factor of 20. More promising are Sequences 7/8, where the gain in signal strength of S- is around a factor of 6 compared with Sequence 1, while the loss in CDC is only a factor of 2-3.

Conclusion

According to this simulation study, it is expected that the design of G_D and G_S in dwDESS has a significant impact on the quality of the resulting diffusion weighted images and ADC map. The optimal design of G_D and G_S depends on the specific requirements of the targeted application.

Acknowledgements

No acknowledgement found.

References

1.	Freed DE et al., Steady-state free precession experiments and exact treatment of diffusion in a uniform gradient. J Chem Phys. 2001;115(9):4249-4258.
2.	Wu EX et al., Effect of diffusion on the steady-state magnetization with pulsed field gradients. J Magn Reson. 1990;90(1):243-253.
3.	Zur Y et al., A new diffusion SSFP imaging technique. Magn Reson Med. 1997;37(5):716–722.
4.	Staroswiecki E et al., Simultaneous Estimation of T2 and ADC in Human Articular Cartilage In Vivo with a Modified 3D DESS Sequence at 3T. Magn Reson Med. 2012;67(4):1086-1096.
5.	Weigel M. Extended phase graphs: dephasing, RF pulses, and echoes - pure and simple. J Magn Reson Imaging. 2015;41(1):266-295.
6.	Keupp J et al., Simultaneous acquisition of diffusion weighted images and conductivity maps using a balanced double echo steady state sequence. Annual Meeting of ISMRM 2020;28:955
7.	Katscher U et al., On the b-value Derivation for diffusion-weighted Double-Echo Steady-State (dwDESS) Magnetic Resonance Imaging. Workshop on Computational Diffusion MRI, MICCAI 2021;12:3