Synopsis

Quantitative microstructural imaging based on diffusion MRI provides a non-invasive means to measure microstructural parameters, e.g., cell size. However, due to the remarkable complexity of incorporating transcytolemmal water exchange into diffusion biophysical models, water exchange is usually ignored. This leads to biased estimation of microstructural parameters, particularly intracellular volume fraction. Here, we propose a new approach to incorporate water exchange naturally in diffusion biophysical models with arbitrary gradient waveforms, making it possible to fit cell size, density, and intracellular water lifetime simultaneously. This establishes a general framework to incorporate transcytolemmal water exchange in any diffusion MRI-based microstructural imaging models.

Introduction

Diffusion MRI (dMRI) provides a non-invasive approach to probe the microstructure in biological tissues. Quantitative information can be further obtained by establishing and fitting biophysical models. Usually, dMRI signal can be expressed as the sum of the signals arising from two compartments¹, i.e., intra- and extra-tissue spaces:
$$S=v_{i n} S_{i n}+v_{e x} S_{e x}=v_{i n} S_{i n}+\left(1-v_{i n}\right) S_{e x}\tag{1}$$
Although Eq. (1) has shown clinical relevance¹, it remains problematic to ignore the transcytolemmal water exchange. The parameters about water exchange have been shown as important indicators of tumor status². Moreover, the ignorance of water exchange has been found to lead to significant underestimation of intracellular volume fraction v_in, making it impossible to estimate cell density non-invasively³.

Karger’s model is usually used to tackle water exchange, but it relies on approximations such as sufficiently long diffusion time and low water exchange⁴. Similarly, Stanisz’s approach needs to implement the short pulse approximation to incorporate water exchange⁵. These approximations are sometimes not valid in clinical acquisitions. To complicate matters, there is increasing interest in modifying diffusion gradient waveforms to include long diffusion gradient pulses for different applications. All these make it very challenging to incorporate water exchange in diffusion biophysical models.

In this work, we propose a general framework to tackle this challenge. First, we discretize any arbitrary-shaped gradient waveforms into a series of short pulses based on multiple propagators⁶. Second, we incorporate Stanisz’s quantitative model⁵ for each short pulse to handle both restricted diffusion and water exchange. Validations on numerical simulations show this new general framework not only enhances the fitting accuracy of microstructural parameters, but also provides additional information related to water exchange.

Theory

The dMRI signals from intra- and extra-cellular spaces are:
$$\begin{gathered}S_{i n}=\exp (-\varphi(t)), \varphi(t)=\frac{\gamma^{2}}{2} \sum_{k} B_{k} \int_{0}^{t} d t_{1} \int_{0}^{t} d t_{2} \exp \left(-a_{k} D_{i n}\left|t_{1}-t_{2}\right|\right) g\left(t_{1}\right) g\left(t_{2}\right) \\S_{e x}=\exp (-\phi(\mathrm{t})), \phi(t)=\gamma^{2} D_{e x} \int_{0}^{t}\left(\int_{0}^{t_{1}} g\left(t_{2}\right) d t_{2}\right)^{2} d t_{1}\end{gathered}\tag{2}$$
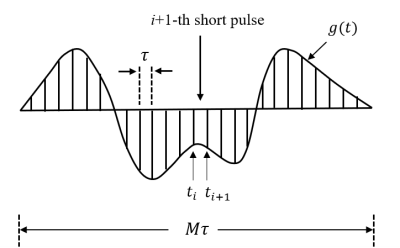
where B_k and a_k are geometric parameters in restricted diffusion. Based on multiple propagators⁶, any arbitrary gradient waveform g(t) can be discretized into a series of short pulses, as shown in Fig. 1.
Because each discretized pulse is short enough, the water exchange can be included in the diffusion biophysical model as⁵:
$$\begin{aligned}\frac{d S_{i n}}{d t} &=-\frac{\varphi\left(t_{i+1}\right)-\varphi\left(t_{i}\right)}{\tau} S_{i n}-K_{i n} S_{i n}+\frac{v_{e x}}{v_{i n}} K_{e x} S_{e x} \\\frac{d S_{e x}}{d t} &=-\frac{\phi\left(t_{i+1}\right)-\phi\left(t_{i}\right)}{\tau} S_{e x}-K_{e x} S_{e x}+\frac{v_{i n}}{v_{e x}} K_{i n} S_{i n}\end{aligned}\tag{3}$$
for t_i≤ t≤ t_i+1, where K_in and K_ex describe the exchange rates. φ(t) and Φ(t) can be computed numerically using Eq.(1). By such a means, we naturally incorporate transcytolemmal water exchange in diffusion biophysical model for any finite-duration, arbitrary-shaped gradient waveforms.

Method

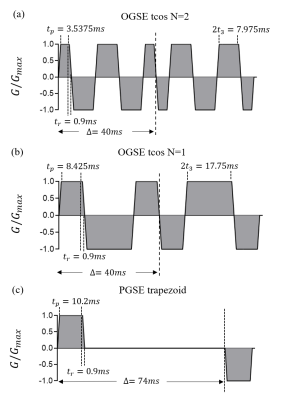
Numerical simulations were performed to evaluate and validate our approach. A finite difference method is used to simulate dMRI signals as reported previously³. The tissue is modeled as tightly packed, spherical cells on a face-centered-cubic lattice with v_in=61.72%, D_in=1.56µm²/ms, and D_ex=2µm²/ms. The cell diameter d is selected from 10~15µm. The intracellular water lifetime, τ_in, is set to 50, 70, 100, 200, 400ms and infinite. K_in and K_ex be computed³ from τ_in, D_in, and d. The used gradient waveforms are shown in Fig. 2, and b-values are (0.25, 0.5, 0.75, 1, 1.25, 1.5, 1.75, 2) ms/μm². Rician noise corresponding to SNR=20 is added into the simulated signals, which is repeated 100 times for each set. Then a fingerprinting-based method as previously reported is used to fit the microstructure parameters⁷.

Results and Discussion

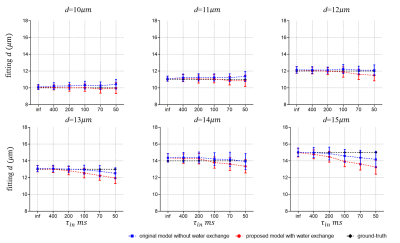
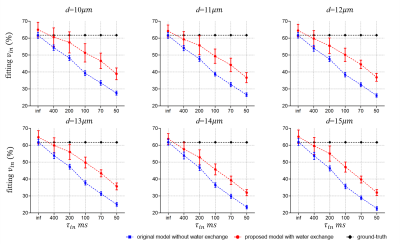
Fig. 3 shows the fitting results of d. There are no statistically significant differences between the diameters extracted from the two models. This is consistent with previous reports that cell size fitting is relatively insensitive to water exchange³.

Fig. 4 shows the fitting results of v_in. As reported previously, the fitted v_in without considering water exchange is significantly underestimated. By contrast, our new approach significantly alleviates such underestimation and provides more accurate fits. However, the fitted v_in with considering water exchange still deviates from the ground-truths and the deviation becomes more pronounced as the rate of water exchange increases (smaller τ_in ). This suggests the impact of water exchange has not been fully incorporated in our proposed approach yet.

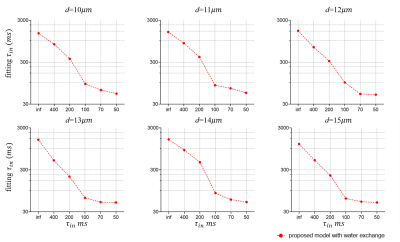
Similarly, the fitting results of τ_in as shown in Fig. 5 do not match perfectly with the ground truths. Presumably, this is also caused by the above reason. However, there is a monotonical correlation between the fitted τ_in and ground truths, suggesting the proposed approach may still provide valuable information on water exchange, which cannot be obtained in conventional microstructural models.

Conclusion

In this work, we propose a general framework to incorporate transcytolemmal water exchange in diffusion biophysical models with arbitrary gradient waveforms. Such an approach can not only improve the fitting accuracy of intracellular volume fraction, but also provide additional information on transcytolemmal water exchange without additional data acquisitions. However, the underestimation of v_in is alleviated but remains, and the fitted τ_in shows a monotonical correlation with ground truths but does not match perfectly. This indicates the impact of water exchange has not been fully incorporated in the biophysical model yet. It is currently under active investigation to further improve the accuracy of this framework.

Acknowledgements

No acknowledgement found.

References

1. Xu J, Jiang X, Li H, Arlinghaus LR, Gore JC. Magnetic resonance imaging of mean cell size in human breast tumors. 2019.

2. Ruggiero MR, Baroni S, Pezzana S, Ferrante G, Geninatti Crich S, Aime S. Evidence for the Role of Intracellular Water Lifetime as a Tumour Biomarker Obtained by In Vivo Field-Cycling Relaxometry. Angewandte Chemie 2018;57(25):7468-7472.

3. Li H, Jiang X, Xie J, Gore JC, Xu J. Impact of transcytolemmal water exchange on estimates of tissue microstructural properties derived from diffusion MRI. Magnetic Resonance in Medicine 2017.

4. Fieremans E, Novikov DS, Jensen JH, Helpern JA. Monte Carlo study of a two-compartment exchange model of diffusion. NMR Biomed, 2010; 23: 711-24

5. Stanisz GJ, Li JG, Wright GA, Henkelman RM. Water dynamics in human blood via combined measurements of T2 relaxation and diffusion in the presence of gadolinium. Magnetic Resonance in Medicine Official Journal of the Society of Magnetic Resonance in Medicine 2010;39(2):223-233.

6. Callaghan PT. A Simple Matrix Formalism for Spin Echo Analysis of Restricted Diffusion underGeneralized Gradient Waveforms. Journal of Magnetic Resonance 1997;129(1):74-84.

7. Baete SH, Cloos MA, Lin YC, Placantonakis DG, Boada FE. Fingerprinting Orientation Distribution Functions in Diffusion MRI detects smaller crossing angles. Neuroimage 2019;198.