4752
An efficient approach for fast signal computation of restricted diffusion with arbitrary gradient waveforms1Center for Nano and Micro Mechanics, Department of Engineering Mechanics, Tsinghua University, Beijing, China, 2Center for Biomedical Imaging Research, Tsinghua University, Beijing, China, 3Institute of Imaging Science, Vanderbilt University Medical Center, Nashville, TN, United States, 4Vanderbilt University Medical Center, Nashville, TN, United States, 5Department of Physics and Astronomy, Vanderbilt University, Nashville, TN, United States, 6Department of Biomedical Engineering, Vanderbilt University, Nashville, TN, United States
Synopsis
Quantitative microstructural imaging based on diffusion MRI usually replies on some simple gradient waveforms, with which analytical expressions can be derived e.g., for fitting cell size. However, it is challenging for this approach for modified irregular gradient waveforms that are increasingly used. Inspired by Callaghan’s matrix formalism, we propose an efficient approach for signal computation with arbitrary gradient waveforms. It can accelerate computation by three orders of magnitude with maintained accuracy, making it feasible in practical data fittings. This work paves the way for quantitative microstructural imaging with arbitrary diffusion gradient waveforms in practice.
Introduction
Quantitative microstructural imaging based on dMRI provides a non-invasive approach to probe cellular microstructural parameters. Typically, tissues are assumed to consist of multiple diffusion compartments with diffusion being either restricted or hindered, respectively. For restricted intracellular diffusion, analytical expressions can be derived to link dMRI signals with different diffusion sequence parameters to underlying cellular morphologic features. This provides a unique opportunity for dMRI mapping microstructural features such as cell size non-invasively. For simple gradient waveforms, such as trapezoid-, sine- and cosine-modulated shapes, analytical expressions can be derived.However, there is an increasing interest in modifying gradient waveforms in dMRI measurements1,2. Then the derivation of corresponding analytical expressions becomes challenging. It is tedious and inefficient to derive analytical expressions for each modified gradient waveform. This significantly increases the complexity to perform quantitative microstructural imaging with modified gradient waveforms.
Here, we propose an efficient approach for fast computation of dMRI signals with arbitrary gradient waveforms. Specifically, this framework (a) incorporates the simple matrix formalism based on multiple propagators to discretize arbitrary waveforms into series of short pulses and (b) uses the dMRI signal attenuation based on velocity correlation function to accelerate signal computation. Our results suggest that this new approach not only accelerates the signal computation by three orders of magnitude compared with Callaghan’s approach3,4, but also achieves high accuracy which was validated by computer simulations and analytical predictions.
Theory
Callaghan’s matrix formulism discretizes any time-varying gradient waveform g(t) into a series of M short pulses each with a duration τ. Because each pulse is short enough, the short pulse approximation holds so that the signal attenuation is given by$$E=\int d \mathbf{r}_{1} \ldots \int d \mathbf{r}_{\mathrm{M}+1} \rho\left(\mathbf{r}_{1}\right) \exp \left(i 2 \pi \mathbf{q}_{1} \cdot \mathbf{r}_{1}\right) P\left(\mathbf{r}_{1} \mid \mathbf{r}_{2}, \tau\right) \ldots \exp \left(i 2 \pi \mathbf{q}_{\mathrm{M}} \cdot \mathbf{r}_{\mathrm{M}}\right) P\left(\mathbf{r}_{\mathrm{M}} \mid \mathbf{r}_{\mathrm{M}+1}, \tau\right) \exp \left(-i 2 \pi \mathbf{q}_{\mathrm{M}+1} \cdot \mathbf{r}_{\mathrm{M}+1}\right)\tag{1}$$
where P(r|r*,Δ) is the propagator. Then E can be computed by the following matrix product
$$E=S\left(\mathbf{q}_{1}\right) R A\left(\mathbf{q}_{2}\right) \ldots R A\left(\mathbf{q}_{M}\right) R S^{+}\left(-\mathbf{q}_{M+1}\right)\tag{2}$$
where S is a vector and R and A are matrixes, whose elements are determined by the propagator P and qi. This approach can convert complex signal computation into a linear problem and, hence, is a plausible solution to handle restricted diffusion with arbitrary waveforms. However, it is not trivial to compute matrix elements with multiple loops of series expansions. This in turns makes the matrix formalism tedious and very time-consuming, infeasible for practical data fittings in quantitative microstructure measurements.
Here, we compute the signal attenuation based on the velocity correlation function developed by Stepisnik5, which has a more concise form
$$\begin{gathered}E=\exp (-\varphi) \\\varphi=\frac{\gamma^{2}}{2} \sum_{k} B_{k} \int_{0}^{T E} d t_{1} \int_{0}^{T E} d t_{2} \exp \left(-a_{k} D\left|t_{1}-t_{2}\right|\right) g\left(t_{1}\right) g\left(t_{2}\right)\end{gathered}\tag{3}$$
where Bk and ak are microstructural coefficients which can be derived for restricted diffusion in simple geometries. Based on the discrete gradient waveform, the computation of φ becomes
$$\varphi=\frac{\gamma^{2}}{2} \sum_{k} B_{k} \sum_{i=1}^{M} \sum_{j=1}^{M} C_{i j}\tag{4}$$
where a symmetric matrix C can be defined as
$$C_{i j}=\int_{t_{i-1}}^{t_{i}} d t_{1} \int_{t_{j-1}}^{t_{j}} d t_{2} \exp \left(-a_{k} D\left|t_{2}-t_{1}\right|\right) g\left(t_{1}\right) g\left(t_{2}\right)\tag{5}$$
Eq.(4) dramatically decreases the computation of signal attenuation by three orders of magnitude compared with Eq.(2). This makes it possible to use this approach to calculate signal attenuation of restricted diffusion with arbitrary gradient waveforms in practical data fitting.
Method
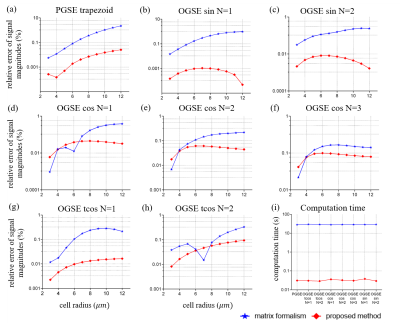
The in-house code was developed in MATLab R2017a. Signal attenuations of restricted diffusion in spherical pores were calculated and compared with the results of the classic matrix formalism3,4 and our approach using several commonly-used gradient waveforms. This makes it possible to use the analytical expressions to evaluate the accuracy of the proposed approach. The tested gradient waveforms and corresponding time parameters are shown in Fig. 2. The computation time tN and the relative error eN, between the numerical computation and the theoretical result, are employed as the evaluation criteria. The diameter of the spherical pore is defined as 6 to 24 μm .Results and Discussion
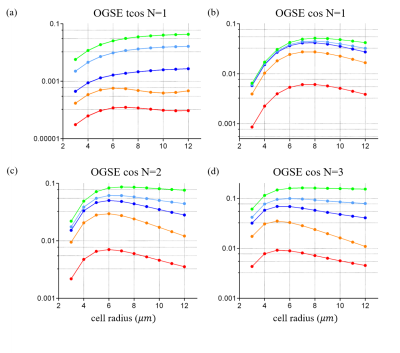
Fig. 3 shows the relative errors and computation times. For the trapezoid-shaped, sine-modulated, and cosine-modulated trapezoidal with N=1 waveforms, the relative errors of the proposed method are significantly lower than that of the matrix formalism. For other waveforms, their relative errors are comparable. However, for all waveforms, the proposed method can shorten the computation time by three orders of magnitude, which makes it suitable for fast computation of restricted dMRI signals for data fittings.Fig. 4 shows the relationship between the relative errors of the proposed generalized method and the discretized temporal steps Δt=TE/M. Δt=0.3ms, that is, M=300 is found to be a good compromise to ensure small relative error (less than 0.1%) with minimal computation time.
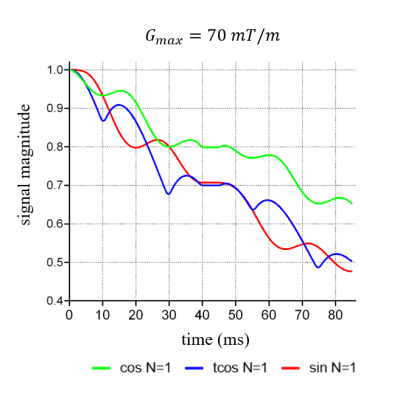
Fig.5 shows additional advantages of our proposed approach, i.e., the proposed method can also provide the evolution of the signal E during the application of gradient waveform, which is infeasible by the analytical expression.
Conclusion
An efficient approach is proposed for fast signal computation of restricted diffusion with arbitrary gradient waveforms. The proposed method not only provides high accuracy but also accelerates the signal computation by three orders compared with the previous method. This work paves the way for quantitative microstructural imaging with arbitrary diffusion gradient waveforms in practice.Acknowledgements
No acknowledgement found.References
1. Topgaard D. Multidimensional diffusion MRI. J Magn Reson, 2017; 275: 98-113.
2. Hennel F, Michael ES, Pruessmann KP. Improved gradient waveforms for oscillating gradient spin-echo (OGSE) diffusion tensor imaging. NMR Biomed, 2021; 34: e4434.
3. Callaghan PT. A Simple Matrix Formalism for Spin Echo Analysis of Restricted Diffusion under Generalized Gradient Waveforms. Journal of Magnetic Resonance 1997;129(1):74-84.
4. Codd SL, Callaghan PT. Spin Echo Analysis of Restricted Diffusion under Generalized Gradient Waveforms: Planar, Cylindrical, and Spherical Pores with Wall Relaxivity. Journal of Magnetic Resonance 1999;137(2):358-372.
5. Stepišnik J. Generalized Analysis of Motion Using Magnetic Field Gradients. Advances in Magnetic and Optical Resonance 1996;19:325-388.
Figures
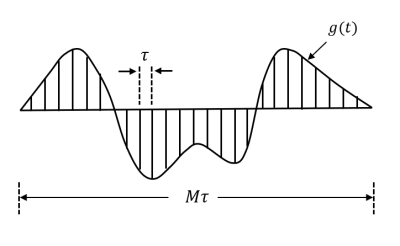
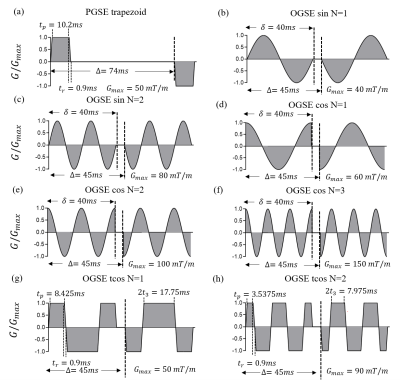
Fig. 2 The diagrams of different finite-length gradient waveforms used for evaluation. (a). trapezoid-shaped PGSE acquisitions (b). sine-modulated OGSE acquisitions with N=1 (sin N=1) (c). sine-modulated OGSE acquisitions with N=2 (sin N=2) (d). cosine-modulated OGSE acquisitions with N=1 (cos N=1) (e). cosine-modulated OGSE acquisitions with N=2 (cos N=2) (f) cosine-modulated OGSE acquisitions with N=3 (cos N=3) (f). cosine-modulated trapezoidal OGSE acquisitions with N=1 (tcos N=1) (f) cosine-modulated trapezoidal OGSE acquisitions with N=2 (tcos N=2).