4738
Physics informed neural networks for phase-based magnetic resonance electrical properties tomography1Medical systems, Chiba University, Chiba, Japan, 2Department of Surgery, National University of Singapore, Singapore, Singapore, 3Engineering Product Development, Singapore University of Technology and Design, Singapore, Singapore, 4Digital Architecture Research Center, National Institute of Advanced Industrial Science and Technology, Tokyo, Japan, 5Center for Frontier Medical Engineering, Chiba University, Chiba, Japan
Synopsis
Magnetic Resonance Electrical Property Tomography (MREPT) could provide important contrast for non-calcified tumors. However, MREPT relies on numerical differentiation, which is noise sensitive and prone to artifacts near boundaries.
In this work, physics-informed neural networks (PINN), NN empowered automatic differentiation is proposed to improve MREPT by mitigating artifacts and reducing noise sensitivity. Instead of calculating partial derivatives numerically, is obtained by backpropagation through PINNs.
For clinical MREPT, reduction of ground-truth information to guide PINNs was investigated. Results show that above 25% collocation points, reconstruction can be made at 100 SNR. PINNs enable noise-robust and artifact-free MREPT from less ground-truth information.
Introduction
Electrical properties are quantitative biomarkers for non-calcified tumorous tissues1,2. Magnetic resonance electrical properties tomography (MREPT) is a technique to reconstruct the electrical properties of tissues from MRI measurements3. The reconstruction formulation is based on Maxwell’s equations. Various methods to reconstruct the conductivity4,5 require the numerical calculation of spatial partial derivatives. Commonly phase-based std-EPT4 calculates numerical derivatives of $$$\phi^{tr}$$$ by parabola fitting6 to reconstruct the conductivity ($$$\sigma$$$). The formulation is shown below.$$\hat\sigma=\frac{\omega\mu_{0}}{\nabla^{2}\phi^{tr}} (1)$$
The numerical calculation of partial derivatives generates boundary artifacts due to numerical errors and is noise sensitive. On the other hand, solvers of partial differential equations by Physics-informed neural networks (PINNs) have been proposed recently7. In [7], the partial differential equation (PDE) to be solved is added to the loss function. Through automatic differentiation frameworks realized by neural networks (NNs), spatial partial derivatives ($$$\nabla^{2}\phi^{tr}$$$) for solving the PDE can be calculated accurately. This method can remove numerical artifacts, and thereby improve the reconstruction accuracy even at high noise levels. However, this method requires collocation points to guide PINNs, which might be difficult for clinical MREPT. In this work, we propose to apply NNs empowered automatic differentiation to phase-based MREPT $$$\sigma$$$ reconstruction and investigate the effect of noise, the percentage of collocation points to be used, and different sources of collocation points: ground truth and estimated conductivity maps using analytic MREPT4,5.
Methods
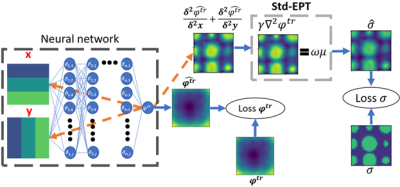
Fig. 1 shows a diagram for the proposed reconstruction method. A set of 2-D spatial kernels are input to the NN, and the NN output are values of $$$\phi^{tr}$$$. The NN is fitted to approximate the $$$\phi^{tr}$$$ simulated values according to the data loss function below,$$Loss \phi^{tr} = MSE(\phi^{tr},\hat{\phi^{tr}}) (2)$$
Next, through automatic differentiation (backpropagation), the partial derivatives concerning the spatial kernels are calculated according to predicted $$$\hat{\phi^{tr}}$$$. As second-order derivatives are needed to solve Eq. 1, the summed results of the first backpropagation are backpropagated once more to produce a second-order derivative kernel and the median value is taken as the derivative value. With the second-order derivative values, $$$\hat\sigma$$$ values can be constructed based on Eq. 1. A second loss function is introduced to match collocation points in ground-truth $$$\sigma$$$, and Eq.1 estimated $$$\hat\sigma$$$.
$$Loss \sigma = MSE(\sigma,\hat\sigma) (3) $$
Both loss functions are summed and minimized by modifying the NN’s parameters according to Adam algorithm8. Two sets of numerical simulations are generated by Sim4Life© as test cases. Test case 1, a binary-value cylinder phantom, and Test case 2, a digital human head phantom “Ella”9. These phantoms were placed in a high-pass 16 rung birdcage-coil excited in quadrature mode at 3T of 14 cm radius and 28 cm length. Region of interest (ROI) $$$\phi^{tr}$$$ is extracted and noise is added according to formulations in the literature10.
Ground truth $$$\sigma$$$ collocation points, and estimated $$$\sigma$$$ by std-EPT or by phase-based stab-EPT11 collocation points are tested.
Results
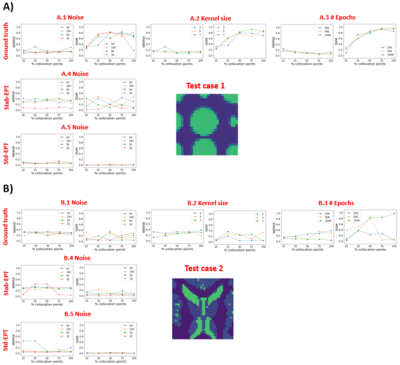
Fig. 2 (a) and (b) show reconstruction results from Test cases 1 and 2, respectively. The percentages of collocation points were tested for reconstructions at 100 SNR. As shown, the reconstruction accuracy increases with the percentage of collocation points. The artifacts contained in std-EPT $$$\sigma$$$ could not provide information to guide the learning of the NN. While stab-EPT $$$\sigma$$$ is a feasible source of collocation points because of its diffusion term11.Fig. 3 shows NRMSE/SSIM (Structural similarity index) values of reconstructed $$$\hat\sigma$$$ w.r.t. the number of collocation points given. The lines indicate various noise levels (SNR = Infinite, 100, 50, 10). The source of collocation points by ground truth $$$\sigma$$$, estimated $$$\sigma$$$ by std-EPT, and stab-EPT, and the number of epochs and size of the input 2-D spatial kernels are investigated. The results match the previous figure results and indicate that with 25% collocation points, reconstructions with above 0.5 SSIM can be made.
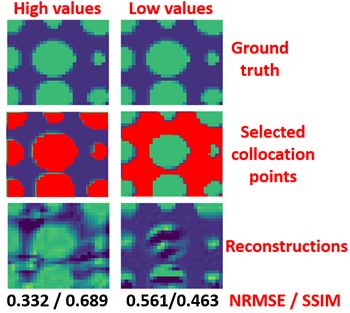
Fig. 4 shows the accuracy when collocation points are provided from either high or low $$$\sigma$$$ from test case 1, the binary-value phantom. Reconstructions of both cases are accurate. Though, small artifacts appeared in loci without collocation points.
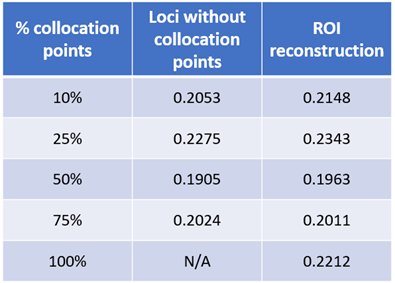
Table 1 shows mean NRMSE values for both test cases at all SNR values of the reconstructed ROI and loci without collocation points. The NRMSE is similar for both conditions. This indicates the method’s robustness to the number of collocation points.
Discussion and conclusion
In this work, PINNs are used to address the noise sensitivity of MREPT’s numerical differentiation. The results indicate that PINNs could accurately calculate partial derivatives for MREPT even in high noise conditions.The fact that 25% of ground truth conductivity as collocation points resulted in reconstruction with high SSIM denotes that MREPT could benefit from the generality of NNs. Using estimated conductivity by stab-EPT as collocation points lead to reconstruction sufficient for anatomical structure, but insufficient for detecting small tissues.
Future work will focus on integrating further physical constraints to increase its accuracy while decreasing the percentage of ground truth conductivity. Finally, due to the interpolation nature of NNs, PINNs may be used to increase the resolution of the imaging by modifying the resolution of the 2-D spatial kernel, which will be further investigated.
Acknowledgements
No acknowledgement found.References
[1] Tha KK, Katscher U, Yamaguchi S, et al. Noninvasive electrical conductivity measurement by MRI: a test of its validity and the electrical conductivity characteristics of glioma. Eur Radiol. 2018;28(1):348-355. doi:10.1007/s00330-017-4942-5
[2] Mori N, Tsuchiya K, Sheth D, et al. Diagnostic value of electric properties tomography (EPT) for differentiating benign from malignant breast lesions: comparison with standard dynamic contrast-enhanced MRI. Eur Radiol. 2019;29(4):1778-1786. doi:10.1007/s00330-018-5708-4
[3] E. M. Haacke, L. S. Petropoulos, E. W. Nilges, and D. H. Wu, “Extraction of conductivity and permittivity using magnetic resonance imaging,” Phys. Med. Biol., vol. 36, no. 6, pp. 723–734, 1991, doi: 10.1088/0031-9155/36/6/002
[4] Katscher U, Findeklee C, Vernickel P, Nehrke K, Voigt T, Dössel O. Determination of Electric Conductivity and Local SAR Via B1 Mapping. IEEE Trans Med Imaging. 2009;28(9):1365-1374. doi:10.1109/TMI.2009.2015757
[5] Li C, Yu W, Huang SY. An MR-Based Viscosity-Type Regularization Method for Electrical Property Tomography. Tomography 2017;3(1):50-59. doi:10.18383/j.tom.2016.00283
[6] Katscher, U., Djamshidi,
K., Voigt, T., Ivancevic, M., Abe, Hi., Newstead, G., Keupp, J., Estimation of
breast tumor conductivity using parabolic phase fitting, Proc. Intl. Soc. Mag.
Reson. Med. 20 (2012), 3482.
[7] Raissi, M., Perdikaris, P., and Karniadakis, G.E., Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations., Journal of Computational Physics, 2019, Vol. 378, pp. 686-707, https://doi.org/10.1016/j.jcp.2018.10.045
[8] D. P. Kingma and J. L. Ba, “Adam: A method for stochastic optimization,” 3rd Int. Conf. Learn. Represent. ICLR 2015 - Conf. Track Proc., pp. 1–15, 2015.
[9] Gosselin M-C, Neufeld E, Moser H, et al. Development of a new generation of high-resolution anatomical models for medical device evaluation: the Virtual Population 3.0. Phys Med Biol. 2014;59(18):5287-5303. doi:10.1088/0031-9155/59/18/5287
[10] F. S. Hafalir, O. F. Oran, N. Gurler, and Y. Z. Ider, “Convection-reaction equation-based magnetic resonance electrical properties tomography (cr-MREPT),” IEEE Trans. Med. Imaging, vol. 33, no. 3, pp. 777–793, 2014, doi: 10.1109/TMI.2013.2296715.
[11] Ider YZ, Akyer MN. Properties and implementation issues of phase-based cr-MRECT for conductivity imaging. In: Proc. Intl. Soc. Mag. Reson. Med. 28. ; 2020:3190. [12]
Figures