Introduction

3D multi-shot diffusion-weighted EPI (3D-msDW-EPI) shows great potential in 3D diffusion-tensor imaging (DTI) because 1) it is feasible to obtain isotopic voxel size with better SNR efficiency compared to 2D acquisition¹, and 2) the in-plane multi-shot acquisition can also alleviate the geometric distortion^2-5. In order to resolve the inter-shot phase variation of 3D-msDW-EPI, 3D multi-slab acquisition and 2D navigator were used¹. However, this method suffers from slab boundary artefacts, and signal corruptions due to through-slab phase variation. 3D-MUSER⁶ succeeded in correcting the inter-shot 3D phase variation by using a 3D single-shot navigator, thereby enabling a nearly whole brain 3D DTI acquired with a single slab at 1.5T. To further improve the acquisition efficiency, compressed sensing (CS)⁷ was successfully incorporated into 3D-MUSER with a pseudo-random under-sampling strategy to achieve improved quality under high acceleration factor⁸. However, a variable-density under-sampling scheme with higher sampling density around k-space origin was suggested to optimize the reconstruction performance for CS MRI⁷ that raises a challenge for 3D-msDW-EPI due to the technical constraints of EPI acquisition. In this study, we propose a variable-density under-sampling strategy for 3D-msDW-EPI to optimize the reconstruction performance using CS, and investigate its feasibility via simulations.

Material and Method

Design of variable-density k-space sampling strategy
As proposed in 3D-MUSER with CS⁸, to retain consistent off-resonance effect between any two adjacent sampling points within an individual in-plane segment of 3D-msDW-EPI, the data sampling along ky must be uniform with a fixed interval. Besides, the maximum gradient blip along kz direction is limited by hardware constraint (e.g., maximum Gzb is 6Δkz) for not causing prolonged EPI echo-spacing. These two requirements restricts the design of k-space trajectories for each shots that raises a challenge to achieve a variable-density sampling pattern after placing all acquired data points at corresponding k-space locations.

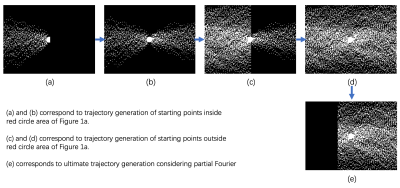
By considering that variable-density sampling allocates more dense points around k-space center, the design of our sampling strategy starts from the k-space center area to generate trajectories for 3D-msDW-EPI. Figure 1a shows the desired sampling points around k-space center (i.e., color dots in the rectangle) that need to be acquired from the EPI echo train center of different shots (i.e., different colors represent the data acquired with different individual ky segments). Starting from each sampling point in the rectangle, the previous and later sampling point will be determined by considering the above two requirements for EPI acquisition. The pseudocode in Figure 1c provides the detailed algorithm for designing the k-space trajectory of each shot to achieve variable-density sampling with a desired under-sampling factor (e.g., R=3). Figures 1a and 1b correspond to the steps 2 and 3 in pseudocode, respectively. Figure 2 illustrates an example of generating a variable-density sampling mask with an acceleration factor of 3 and a partial-Fourier factor of 64.58%. The complete k-space trajectories of each shots will be recorded, and the data acquisition of each shot will start from the minimum ky to maximum ky locations. Consequently, the pulse sequence of 3D-MUSER can be further modified to collect real 3D multi-shot DWI data with variable-density sampling according to the designed trajectories.

Data simulation and reconstruction
3D single-slab whole brain DTI data with 15 diffusion directions (matrix size=144*192) were used to simulate the data acquisition with variable-density sampling (R=3, total number of shots=192), partial Fourier (64.58%), and the presence of inter-shot 3D phase variations. The reconstruction method followed previously proposed method⁸ that incorporated compressed sensing into 3D-MUSER by solving $$$\underset{\rho}{\operatorname{argmin}}\|F \phi C \rho-S\|_{2}^{2}+\lambda\|\Psi \rho\|_{1}$$$ using the nonlinear conjugate gradient decent algorithm, where $$$C$$$, $$$\phi$$$, $$$F$$$, $$$S$$$, $$$\Psi$$$, $$$\lambda$$$ represent coil sensitivity, inter-shot 3D phase variations, 2D Fourier Operator, segment k-space signal, 2D wavelet operator, and regularization parameter respectively.

Results

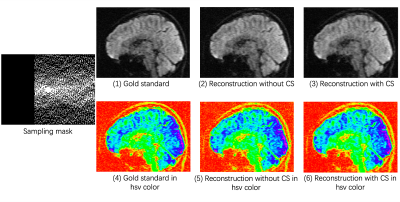
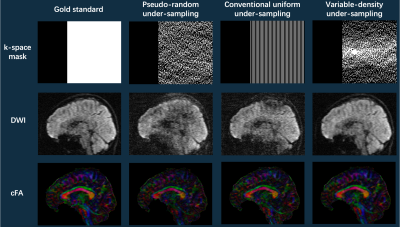
Figure 3 compares the reconstruction results of data acquired with variable-density sampling using either originally proposed 3D-MUSER⁶ or 3D-MUSER with CS. Figure 4 compares the representative DWI images reconstructed from the data acquired with different sampling strategies (i.e., previously proposed pseudo-random under-sampling⁸, conventional uniform under-sampling, and our variable-density under-sampling), and the corresponding color-FA maps.

Discussion and Conclusion

We propose a novel design method that starts from the desired sampling point around k-space center to achieve a variable-density under-sampling patterns for 3D-msDW-EPI, under the pre-defined acquisition constraint. The simulation results demonstrate that our under-sampling strategy for 3D DTI acquisition could better convert the aliasing problem to a noise problem which could be eliminated by using CS. The proposed variable-density under-sampling with CS produced superior results to the data acquired with a pseudo-random under-sampling for 3D-MUSER. Although the proposed sampling strategy shows comparable quality to gold-standard image during simulations, an implementation on MRI scanner and in-vivo test are needed for further investigation of its feasibility. In conclusion, the proposed variable-density under-sampling for 3D-MUSER and CS may be a promising solution to enable 3D DTI acquisition with high acceleration factors, thereby improving the acquisition efficiency without the expense of data quality.

Acknowledgements

The work was in part supported by grants from Hong Kong Research Grant Council (GRFs 17121517, 17106820, and 17125321).