Introduction

Magnetic resonance imaging (MRI) is a widely used imaging modality in clinical diagnosis. However, its long scanning time will lead to motion artifacts. Under-sampling in k-space is a common solution, but aliasing artifacts will appear in the reconstructed images. Recently, many deep learning-based approaches have been proposed to solve this problem. However, most of these methods rely on a large number of fully-sampled MRI to train the network. In fact, the fully-sampled MR images are difficult to obtain since it is time-consuming. To solve this issue, Yamen et al.¹ developed a framework using self-supervised learning via data undersampling (SSDU) for training a network without fully-sampled datasets. Hu et al.² proposed a parallel self-supervised learning framework. However, acquired under-sampled measurements are still not sufficiently utilized. Thus, we proposed a self-supervised triple network framework (SSTN) with multi-scale dilated-convolution to solve the above question.

Method

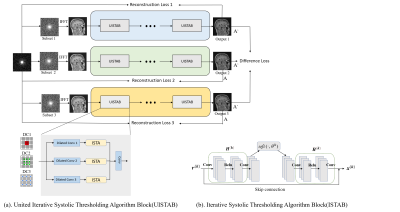
The framework of SSTN is illustrated in Figure 1. It consists of three major parts: 1) The same under-sampling mask and different selection masks; 2) three parallel networks consisting of multiple UISTA Block individually; 3) the output results of each parallel branch and the difference loss is calculated between the output result of the three networks
Mathematical Model
Overall, the problem solved during the training phase can be written in a mathematical formula as:
$$\begin{gathered}\arg \min _{\mathrm{x}_{1}, \mathrm{x}_{2}, \mathrm{x}_{3}} \frac{1}{2}\left(\left\|A_{1} x_{1}-y_{1}\right\|_{2}^{2}+\left\|A_{2} x_{2}-y_{2}\right\|_{2}^{2}+\left\|A_{3} x_{3}-y_{3}\right\|_{2}^{2}\right)+\lambda R\left(x_{1}\right)+\mu R\left(x_{2}\right)+v R\left(x_{3}\right) \\+\xi L\left(x_{1}, x_{2}, x_{3}\right)\end{gathered}$$
where $$$A$$$ denotes the encoding matrix obtained from the dot product of the sampling matrix $$$S$$$ and the Fourier transform $$$F$$$, $$$y$$$ denotes the image output by selection mask, $$$L$$$ denotes similarity metrics, $$$x_{1}, x_{2}$$$ and $$$x_{3}$$$ are the three reconstruction results from three parallel network. $$$R$$$ represents $$$L1$$$ regularization, and $$$\lambda, \mu, v, \xi$$$ are regularization parameters.
Mask Details
Selection mask and under-sampling mask are employed. The under-sampling mask is used to generate under-sampled images. The selection mask picks random points from the under-sampled data to generate the image as the input reconstruction network. The masks we used in study are shown in Figure 2.
UISTA Block
As shown in Figure1(a) the UISTA Block consists of three parallel unrolled versions of the ISTA-Net³. The front end of each net is connected to a multi-scale dilated convolutional layer in this block, and a traditional convolutional layer is at the end of this block. The optimization of the image reconstruction problem is solved by iterating the following two steps in UISTA Block:
$$\begin{aligned}\mathbf{r}^{(k)} &=\mathbf{x}^{(k-1)}-\rho \mathbf{A}^{\top}\left(\mathbf{A} \mathbf{x}^{(k-1)}-\mathbf{y}\right) \\\mathbf{x}^{(k)} &=\widetilde{\mathcal{H}}\left(\operatorname{soft}\left(\mathcal{H}\left(\mathbf{r}^{(k)}\right), \theta\right)\right)\end{aligned}$$
where $$$n$$$ is the serial number of ISTA-Net in the UISTA block, $$$\rho$$$ is the step size, $$$k$$$ represents the iteration index, $$$\mathcal{H}$$$ and $$$\widetilde{\mathcal{H}}$$$ denotes a combination of two linear convolutional operators and a rectified linear unit (ReLU).
Loss Function Design
The loss function in this paper is defined as:
$$\begin{aligned}L(\Theta)=\frac{1}{N}\left(\sum_{i=1}^{N}\right.&\left(L\left(y^{i}, A^{i} x_{1}^{i}\right)+L\left(y^{i}, A^{i} x_{2}^{i}\right)+L\left(y^{i}, A^{i} x_{3}^{i}\right)\right) \\&\left.+\alpha \sum_{i=1}^{N}\left(L\left(A^{\prime i} x_{1}^{i}, A^{i \prime} x_{2}^{i}\right)+L\left(A^{\prime i} x_{1}^{i}, A^{i \prime} x_{3}^{i}\right)\right)+\beta L_{cons1}+\gamma L_{cons2}+\delta L_{cons3}\right)\end{aligned}$$
where $$$N$$$ is the number of the training cases, $$$i$$$ is the current training case, $$$L$$$ refers to the MSE loss, $$$A$$$ and $$$A^{\prime}$$$ respectively represent the scanned and unscanned k-space data points, $$$L_{cons}$$$ represents constraint loss.

Dataset

Public Campinas brain MR raw data were used for training. Randomly selected 40 subjects for network training and 2 subjects for testing, corresponding to 2800 and 140 2D images, respectively. The matrix size of each image is 256×256.

Experimental Settings and Evaluation

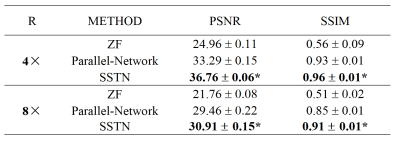
The proposed SSTN was tested on data with 2D random under-sampling under 4x and 8x acceleration factors. We evaluated the performance of the SSTN against previously proposed Parallel-Network² and ablation experiments were performed. We trained the networks with the following hyperparameters: $$$\alpha, \beta, \gamma, \delta$$$=0.01 for SSTN reconstruction. The model used a batch size of 2 and the initial learning rate of 10^-4 for training. Experiments were carried out a system equipped with GPUs of NVIDIA Quadro GP100 (with a memory of 16GB). We evaluated the reconstruction results quantitatively in terms of PSNR and SSIM. A paired Wilcoxon signed-rank test was conducted to compare the PSNR and SSIM measurements between different approaches. p < 0.05 was treated as statistically significant.

Results

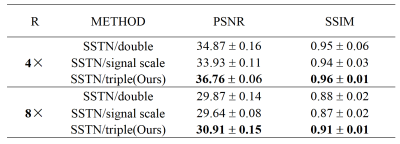
As shown in Figure 3, the ZF reconstruction was remarkably blurred. Moreover, the Parallel Network reconstructed images contained substantial residual artifacts, which can be seen in the error maps. However, the SSTN results had the least error and were capable of removing the aliasing artifacts. Correspondingly, the proposed SSTN method also performed the best in terms of PSNR and SSIM metrics. These observations have a good correlation with the numerical analysis shown in Table 1.
Meanwhile, the results in Table 2 verified that the multi-scale dilated convolution can extract features more efficiently and improve the reconstruction quality. Furthermore, the triple network structure in SSTN will constrain the reconstruction results of each network more efficiently.

Conclusion

The proposed SSTN can generate better quality reconstructions than competing methods at high acceleration rates. Thus, the proposed SSTN is promising for under-sampled MRI reconstruction in many clinical applications, where no fully-sampled data are available for complete training.

Acknowledgements

This work was supported by the National Natural Science Foundation of China ( No. 61902338, No. 62001120), the Shanghai Sailing Program (No. 20YF1402400).