INTRODUCTION

Propeller FSE-DWI¹ has been a method of choice in particular for Cholesteatoma², since it is robust to skull base susceptibility artifact. However, its natures such as prolong scan time, low signal-to-noise ratio (SNR), and phase variations among the blades have been challenging. Typically, SNR can be gained by shortening TE, which can be done by reducing echo train length (ETL) with the expenses of prolong acquisition time due to more blades are required. Parallel imaging technique³ can be applied to reduce scan time, but phase estimation/correction is often compromised due to g-factor noise penalty. In this work, we aim to implement an iterative reconstruction with locally low rank⁴ (LLR) regularization without requiring phase calibration, to maximize quality of SENSE-4 propeller FSE-DWI images.

METHODS

Discrete single-blade signal model: A single-blade signal measured during readout $$$m\in[0\,M]$$$ of phase encoding line $$$n\in[0\,N]$$$ can be modeled as:
$$g_{c,α}[m,n]=\sum_{p=0}^{P-1}\sum_{q=0}^{Q-1}s_c [p,q]u[p,q]e^{(-j(k_{x.α}[m]p+k_{y,α}[n]q)}+ε_{c,α}[m,n]\;\;\;\;(1)$$
where $$$p\in[0\,P-1]$$$ and $$$q\in[0\,Q-1]$$$ are pixel indices. $$$u$$$ is underlying image, $$$k_{x,α}$$$ and $$$k_{y,α}$$$ are the k-space coordinates in the readout and phase-encoding dimensions associated with blade angle $$$α\in[0\,N_α]$$$. $$$s_c$$$ is the sensitivity profile for coil $$$c\in[0\,C\!-1]$$$ , $$$ε$$$ and is white Gaussian noise. Defining $$$S=[diag{S_0}⋯diag{S_{C\!-1}}]^T∈\mathbb{C}^{PQ×C}$$$, Eq.(1) abstracts to:
$$G_α=(I⨂F_α)Su_α+Ɛ_α=A_αu_α+Ɛ_α\;\;\;(2)$$
Where $$$F_α∈\mathbb{C}^{MN×PQ}$$$ is either fully or under-sampled Fourier transform (or NUFFT-II) and $$$\bigotimes$$$ is Kronecker’s product.
Joint blade reconstruction with locally low rank regularization: In LLR^4,5, a set of target images ($$$u_α$$$) are obtained by minimizing the following convex cost function.
$$\min_{\{{u_1,...,u_{N_α}}\}\in\mathbb{C}}\beta\sum_{b\inΨ}\parallel\!R_b\sum_{α=1}^{N_α}u_α\delta\,_α^T\parallel_*+\sum_{α=1}^{N_α}\parallel\!A_α u_α-G_α\parallel_2\;\;\;(3)$$
$$$\beta$$$ is a regularization parameter. $$$\delta$$$ is Kronecker delta. Operator $$$R$$$ extracts the $$$b_{th} (B^2×N_α)$$$ blocks from the set $$$ψ$$$ and reshapes each block into Casorati matrix. The nuclear norm ($$$\parallel\cdot\parallel_*$$$) is the convex envelope of the rank functional. The optimization problem in (3) can be solved using fast composite splitting algorithm (FCSA)⁶, a generalization of the Fast Iterative Shrinkage Algorithm (FISTA) that allows independent management of penalties, which herein coincides with block-wise singular value thresholding (SVT) of the augmented Casorati matrices along with nominal blade blocks.
Data Acquisition and Processing: In-vivo experiments were performed on 1.5T MRI (Ingenia; Philips, Best, the Netherlands) equipped with 12-channel receiver head coil. Single volunteer was scanned after informed consent according to institutional review board-approved (IRB) protocol. A vendor provided Multivane TSE-DWI (b-value 0, 1000 mm.2/sec.) was employed with following parameters: FOV = 220 mm.2, readout samples 116, slice thickness 4 mm.,12 ETLs, 12 blades (0-180° with 15° interval), SENSE-factor of 4, scan time 3.5 minutes. In addition, coil sensitivity maps were estimated form single-shot TSE data (scan time 12 seconds) using the ESPIRiT7. Image reconstruction was performed in Matlab using 30 iterations of FISTA with manually optimized (, block-size 7⨯7, 2X-oversampled type-II NUFFT8 with a width J=5 Kaiser-Bessel kernel.

RESLUTS

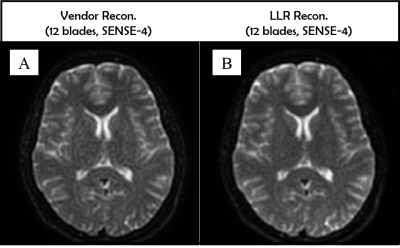
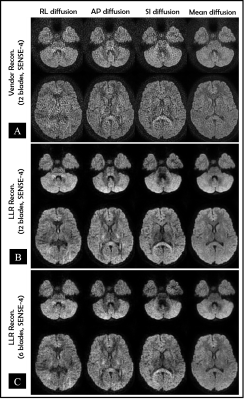
In Figure 1A- 1B, b0-value images obtained by vendor’s provided reconstruction appear slightly more noise than the LLR reconstruction (by visual inspection). In Figure 2A-2C, b1000-value images obtained by vendor’s provided reconstruction are highly corrupted by noise (Figure 2A), while LLR reconstruction enables to clean up those noise successfully (Figure 2B). Moreover, when data are artificially subsampled by half (Figure 2C), in which only 6 blades (0-180° with 30° interval) were incorporated in the LLR reconstruction, the reconstructed images still look slightly better than the images obtained by vendor’s provided reconstruction (12 blades).

DISCUSSIONS

Typically, vendor’s provided reconstruction engine for Propeller/Multivane TSE-DWI comprises several steps including motion estimation and correction, per blade phase estimation and correction, and all blades combination with intensity compensation. Phase estimation form highly under-sampled data may fail due to g-factor noise penalty and propagate into the final reconstructed images as shown in Figure 1. For high SNR data (i.e., b0-value), this issue is likely to be negligible. The LLR constraint exploits the low rank property of image similarity in small blocks across multiple blades, thereby recovering full image without using explicit prior knowledge of phase information. Moreover, radial sampling type provides sufficient useful information even with small blade numbers due to its high redundancy of data at center of k-space. This advantage with LLR reconstruction provided good suggestion for scan time reduction as demonstrated in Figure 2C. Finally, low rank modelling⁹, MUSSELS¹⁰ or ALOHA¹¹, may be also practical for this type of acquisition.

Acknowledgements

This work was financially supported by Chiang Mai University, Thailand