4711

Physics-based data-augmented deep learning without fully sampled dataset for multi-coil magnetic resonance imaging

Ruoyou Wu¹, Chen Hu¹, Cheng Li¹, Wenxin Fan¹, Hairong Zheng¹, and Shanshan Wang¹
¹Paul C. Lauterbur Research Center for Biomedical Imaging, Shenzhen Institute of Advanced Technology, Chinese Academy of Sciences, Shenzhen, China

Synopsis

Self-supervised deep learning for MR reconstruction has shown high potential in accelerating MR imaging as it doesn’t need fully sampled dataset for model training. However, the performances of the current self-supervised methods are limited as they don’t take full utilization of the available under-sampled data. We propose a physics-based data-augmented deep learning method to enable faster and more accurate parallel MR imaging. Novel augmenting losses are calculated, which can effectively constrain the model optimization with better utilization of the collected dataset. Extensive experiments are conducted, and better reconstruction results are generated by our method compared to the current state-of-the-art methods.

Introduction

Magnetic resonance imaging (MRI) is widely used for the diagnosis of various diseases. One bottleneck of MRI is the long scan time when compared to other medical imaging techniques, such as computed tomography (CT). Parallel MRI is a widely utilized acceleration strategy that exploits redundant information provided by multiple receiving coils to reduce the scan time^1-3. Recently, deep learning has been widely used for MR image reconstruction due to its excellent performances⁴. For purely data-driven methods, mappings between under-sampled data and fully sampled data or between images with artifacts and artifact-free images are usually learned^5,6. To increase the method interpretability, physics-guided approaches are proposed, and inverse problems with regularized least squares objective functions are usually solved^7-10. These models mainly adopt the fully supervised learning method, which require fully sampled data as references during model optimization. Despite the achieved successes, it is difficult to obtain fully sampled data in real-world applications, especially when dynamic imaging is performed. Self-supervised learning method can solve this problem and encouraging performances have been reported¹¹. However, the performance can still be improved due to the low efficiency on the utilization of the collected data. To enable faster and more accurate parallel MR imaging, we propose a novel physics-based data-augmented deep learning approach, which improves data utilization efficiency.

Methodology

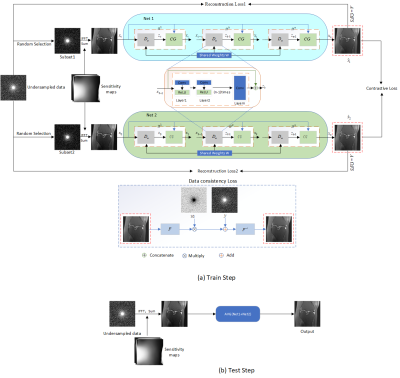
The overall framework of our proposed method is shown in Figure 1. During model training, two networks are optimized in parallel. Accordingly, two reconstruction losses are calculated. Besides, contrastive representation learning is used and a contrastive loss is calculated to force the generation of consistent reconstruction results of the two networks. In addition, to facilitate the reconstruction of high-quality images from the under-sampled data, we designed a data consistency loss, which is calculated by the following formula: $$\ell_{dc}(\hat{x})=\ell(\hat{x},(F\hat{x}(1-Ω)+y)F^{-1})$$ Where, $$$\ell(x,y)=1-SSIM(x,y)+MSE(x,y)$$$, $$$\hat{x}$$$ represents the reconstructed output. $$$F^{-1}$$$ represents the two-dimensional inverse Fourier transform. Two data consistency losses are calculated. In total, there are five loss terms: $$ \xi(\hat{x_{1}},\hat{x_{2}})=\frac{1}{N}\left\{\displaystyle\sum_{i=1}^N\ell(A\hat{x}_1^i,y^{i})+\displaystyle\sum_{i=1}^N\ell(A\hat{x}_2^i,y^{i})\right\}+\frac{1}{N}\left\{\displaystyle\sum_{i=1}^N\ell_{dc}(\hat{x}_1^i)+\displaystyle\sum_{i=1}^N\ell_{dc}(\hat{x}_2^i)+\displaystyle\sum_{i=1}^N\ell_{cl}(\hat{x}_1^i,\hat{x}_2^i)\right\} $$ Where, $$$N$$$ is the total number of training samples. $$$i$$$ represents the i-th training sample. $$$\ell_{cl}(\cdot)$$$ represents contrastive loss. $$$\hat{x}_{1}^{i}$$$ and $$$\hat{x}_{2}^{i}$$$ are the outputs of two networks, respectively. The publicly available dataset, fastMRI Knee dataset, is employed to validate the effectiveness of our proposed method. The dataset includes data collected utilizing two pulse sequences, yield coronal proton-density weighting with (PD-FS) and without (PD) fat suppression. Two evaluation metrics are reported, PSNR and SSIM. Higher PSNR and SSIM values indicate better reconstruction results.

Results and Discussion

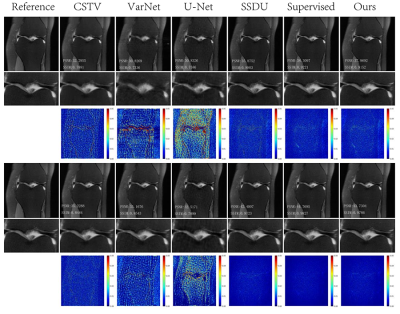
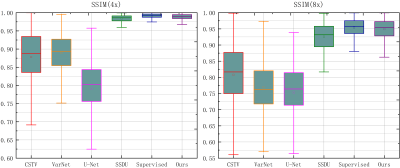
Reconstruction results of different methods under two acceleration rates (R=4 and R=8) are reported. Figure 2 and Figure 3 plot the reconstructed images as well as residual error maps of different methods (CSTV, VarNet, U-NET-256, SSDU, Supervised-MoDL, and Ours). Figure 4 and Figure 5 give the quantitative results (PSNR and SSIM). Both reconstructed images and calculated evaluation metrics verify that our proposed self-supervised method can generate better reconstruction results than the other methods except for the Supervised-MoDL method, which is a fully supervised method. Moreover, our method can perform on par with the Supervised-MoDL method.

Conclusion

In this study, a physics-based data-augmented deep learning model is proposed, which achieves faster and more accurate parallel MR imaging by better utilizing the augmented under-sampled dataset with a co-training and parallel framework.

Acknowledgements

This research was partly supported by Scientific and Technical Innovation 2030-"New Generation Artificial Intelligence" Project (2020AAA0104100, 2020AAA0104105), the National Natural Science Foundation of China (61871371, 81830056), Key-Area Research and Development Program of GuangDong Province (2018B010109009), Key Laboratory for Magnetic Resonance and Multimodality Imaging of Guangdong Province(2020B1212060051), the Basic Research Program of Shenzhen (JCYJ20180507182400762), and Youth Innovation Promotion Association Program of Chinese Academy of Sciences (2019351).

References

[1] Pruessmann KP, Weiger M, Scheidegger MB, et al. SENSE: Sensitivity encoding for fast MRI. Magnetic Resonance in Medicine. 1999; 42(5): 952-962.

[2] Griswold MA, Jakob PM, Heidemann RM, et al. Generalized auto-calibrating partially parallel acquisitions (GRAPPA). Magnetic Resonance in Medicine. 2002; 47(6): 1202-1210.

[3] Lustig M, Pauly JM. SPIRiT: Iterative self-consistent parallel imaging reconstruction from arbitrary k-space. Magnetic Resonance in Medicine. 2010; 64(2): 457-471.

[4] Knoll F, Hammernik K, Zhang C, et al. Deep-learning methods for parallel magnetic resonance imaging reconstruction: A survey of the current approaches, trends, and issues[J]. IEEE signal processing magazine, 2020; 37(1): 128-140.

[5] Lee D, Yoo J, Tak S, et al. Deep residual learning for accelerated MRI using magnitude and phase networks. IEEE Transactions on Biomedical Engineering. 2018; 65(9): 1985-1995.

[6] Han Y, Sunwoo L, Ye JC. K-space deep learning for accelerated MRI. IEEE Transactions on Medical Imaging. 2020; 39(2): 377-386.

[7] Hammernik K, Klatzer T, Kobler E, et al. Learning a variational network for reconstruction of accelerated MRI data. Magnetic Resonance in Medicine. 2018; 79(6): 3055-3071.

[8] Zhang J, Ghanem B. ISTA-Net: Interpretable optimization-inspired deep network for image compressive sensing. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, Utah, 2018.pp 1828-1837.

[9] Mardani M, Sun Q, Donoho D, et al. Neural proximal gradient descent for compressive imaging. Adv Neural Inf Process Syst. 2018; 9573-9583.

[10] Aggarwal HK, Mani MP, Jacob M. MoDL: Model-based deep learning architecture for inverse problems. IEEE Transactions on Medical Imaging. 2018; 38(2): 394-405.

[11] Yaman B, Hosseini SAH, Moeller S, et al. Self-supervised learning of physics-guided reconstruction neural networks without fully sampled reference data. Magnetic resonance in medicine. 2020; 84(6): 3172-3191.

Figures

Fig.1. The framework of our proposed physics-based data-augmented deep learning model. (a) Model training. Two random subsets are selected from the under-sampled data, which are treated as the two inputs to the parallel networks. Five losses are calculated, including two reconstruction losses of $$$\hat{x}_1$$$ and $$$\hat{x}_2$$$, two data consistency losses of $$$\hat{x}_1$$$ and $$$\hat{x}_2$$$, and a contrastive loss between the two. (b) Model testing. The average of $$$\hat{x}_1$$$ and $$$\hat{x}_2$$$ is taken as the final result.

Fig.2. Reconstruction results of an example test slice from the fastMRI coronal proton density (PD) knee MRI dataset under the acceleration rates of R = 4 (top) and R = 8 (bottom). The fully sampled images are shown in the first column for reference. The second to the last columns give the reconstructed images of CSTV, VarNet, U-Net, SSDU, Supervised-MoDL, and Ours, respectively. Except for the Supervised-MoDL method, ours proposed self-supervised method generates better results.

Fig.3. Reconstruction results of an example test slice from the fastMRI coronal proton density weighted with fat suppression (PD-FS) dataset under the acceleration rates of R = 4 (top) and R = 8 (bottom). The fully sampled images are shown in the first column for reference. The second to the last columns give the reconstructed images of CSTV, VarNet, U-Net, SSDU, Supervised-MoDL, and Ours, respectively. Similarly, except for the Supervised-MoDL method, ours proposed self-supervised method generates better results.

Fig.4. Box plots showing the median and interquartile range (25th-75th percentile) of PSNR calculated using the test data. Our proposed self-supervised method, supervised-MoDL, and SSDU give higher PSNR values than CSTV, VarNet, and U-Net. Our method generates very close results to supervised-MoDL, which is a fully supervised method.

Fig.5. Box plots showing the median and interquartile range (25th-75th percentile) of SSIM calculated using the test data. Similarly, our proposed self-supervised method, supervised-MoDL, and SSDU give higher SSIM values than CSTV, VarNet, and U-Net. Our method generates very close results to supervised-MoDL, which is a fully supervised method.

Proc. Intl. Soc. Mag. Reson. Med. 30 (2022)

4711

DOI: https://doi.org/10.58530/2022/4711