Introduction

The emerging wave encoding methods exploit the coil sensitivity variation in the readout dimension for highly accelerated parallel imaging^[1-3]. They are typically achieved by applying wave gradients (i.e., sinusoidal trajectory) in phase or/and partition dimensions to spread the aliasing along the readout direction. However, gradient trajectory is often preset in these existing wave encoding methods and non-specific to receiver array coil. We develop a numerical procedure to optimize the wave gradient trajectory for a given coil sensitivity so to significantly increase acceleration and decrease maximum gradient slew rate. It minimizes the squared L2-norm of off-diagonal elements in the encoding correlation matrix. This matrix reflects the g-factor noise penalty and is determined by the wave gradients, coil sensitivity, and undersampling pattern^[4,5]. Further, this optimization includes a bandlimited constraint in the frequency domain, enabling a smooth trajectory and moderate slew rate in the time domain.

Theory and Method

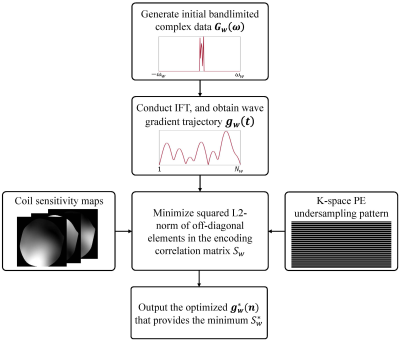
Wave gradient trajectory optimization
The squared L2-norm of off-diagonal elements in the correlation matrix is calculated as^[5]:
$$S_{w}=\sum_{j=1}^{N_{y}/R}\sum_{m=1}^R\sum_{n=1}^R\sum_{i=1}^L\left\|C_{i,(j+m)}^HF_x^HPSF_{j+m}^HPSF_{j+n}F_{x}C_{i,(j+n)}\right\|_2^2 (1)$$
where N_y is the number of phase encoding lines, L the number of channels, and R the acceleration factor. $$$C_{i,(j+m)}$$$ or $$$C_{i,(j+n)}$$$ is a diagonal matrix with the elements being the ith channel and (j+m)th or (j+n)th row of the coil sensitivity maps (i = 1, ..., L; j = 1, ..., N_y; n, m = 1, ..., R and n ≠ m). $$$PSF_{j+m}$$$ or $$$PSF_{j+n}$$$ is a diagonal matrix with the elements being the (j+m)th or (j+n)th row of Point Spread Function (PSF), which is calculated as $$$PSF_{j+m}=e^{-i\gamma(j+m)\sum{g_{w}(t)}}$$$ and $$$PSF_{j+n}=e^{-i\gamma(j+n)\sum{g_{w}(t)}}$$$, where $$$g_{w}(t)$$$ is the gradient trajectory. $$$F_{x}$$$ represents the Fourier transform along x (readout) dimension. Generally, small off-diagonal elements of the correlation matrix result in decreased g-factors^[5]. Therefore, the optimization is to find the wave gradients that have the minimum value of S_w.
The main optimization steps are illustrated in Fig. 1. First, we randomly generate an initial bandlimited complex data ($$$G_{w}(\omega)$$$) in the frequency domain, and conduct inverse Fourier transform to obtain the wave gradient trajectory ($$$g_{w}(t)$$$) in the time domain. Afterward, with the gradient trajectory, sensitivity maps, and undersampling pattern, the squared L2-norm of the off-diagonal elements in the correlation matrix (S_w) is calculated according to Eq. (1) and then optimized. Finally, the optimized $$$g_w^*(t)$$$ owning the minimum S_w^* is obtained.
Simulation experiments
Simulation experiments were conducted with various acceleration factors and slice locations. Fully sampled 2D brain T2-weighted data were acquired on a Philips 3T MR system with an 8-channel head coil. The 2D FSE sequence parameters were: TE/TR = 113ms/3000ms, bandwidth = 246Hz/pixel, FOV = 240×240mm², in-plane resolution = 1×1mm², slice thickness = 4mm, ETL = 20, readout oversampling factor = 2.
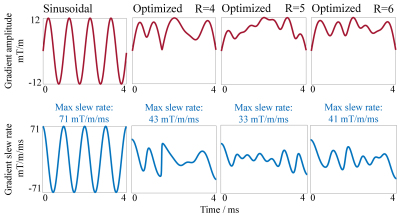
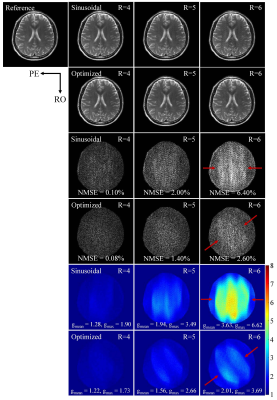
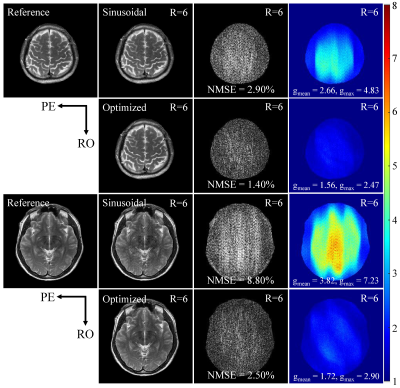
For comparison, a conventional sinusoidal wave encoding gradient was used (i.e., incorporated into phase encoding direction) with typical parameters: wave cycle = 4, maximum wave gradient = 11.55 mT/m (2× readout gradient amplitude)^[7,8]. For the proposed optimization, the maximum gradient was kept the same. The theoretical PSFs were calculated using the above-generated gradients trajectories. Wave encoded data were simulated based on the fully sampled k-space data and PSF^[8]. In all simulation experiments, acceleration was implemented through uniform undersampling in phase encoding steps retrospectively^[5]. Also, the central 24 lines were utilized to estimate the sensitivity maps. The ESPIRiT algorithm was used for image reconstruction^[7]. The g-factor maps were calculated using the pseudo-multiple replica method.

Results

The proposed optimization achieves consistent improvements in reducing noise amplification, i.e., g-factors, for various accelerations (Fig. 3) and slice locations (Fig. 4). The improvement is particularly significant at very high acceleration factors (R=6; see Figs. 3 and 4). The error maps and g-factor maps exhibit very different patterns for sinusoidal and optimized trajectories (see Fig. 3 as indicated by red arrows). This illustrates the coil sensitivity specific control of aliasing by the optimized trajectory, which leads to the reduction in residual artifacts and g-factors. In addition, given the same maximum gradient amplitude, the optimized trajectory requires a lower maximum gradient slew rate than the sinusoidal trajectory as shown in Fig. 2. These results demonstrate that the optimized gradient trajectory significantly outperforms the traditional sinusoidal trajectory.

Discussion and Conclusions

The proposed method offers a new way to further accelerate wave encoding parallel imaging by coil sensitivity specific optimization of wave encoding gradient trajectory (i.e., optimization of 2D PSF for minimizing noise propagation when unfolding aliasing during parallel imaging reconstruction). Significant improvement is demonstrated in g-factor reduction at very high acceleration. Note that residual artifacts can be further reduced in practice by increasing the gradient amplitude or using virtual conjugate coils^[5]. The bandlimited constraint in the proposed optimization procedure imposes not only low slew rate but also high optimization efficiency. It corresponds to fewer optimization variables in the frequency domain than in the time domain, thus resulting in more efficient optimization. Moreover, this work can be extended to the 3D wave encoding parallel imaging. For example, with two gradient trajectories and acceleration in two dimensions, Eq. (1) can be modified by replacing the 2D PSF matrix with a 3D PSF matrix, and incorporating a correlation matrix of aliasing lines in both dimensions.

Acknowledgements

The authors thank Porf. Dong Liang, Prof. Haifeng Wang and Dr. Zhilang Qiu for earlier and insightful encouragement and discussions. The authors also thank Prof. Berkin Bilgic for sharing the codes online at http://martinos.org/∼berkin/software.html. The authors also thank Porf. Dong Liang, Prof. Haifeng Wang and Dr. Zhilang Qiu for insightful discussions. This work was supported in part by Hong Kong Research Grant Council (R7003-19F, HKU17112120 and HKU17127121 to E.X.W., and HKU17103819, HKU17104020 and HKU17127021 to A.T.L.L.), Lam Woo Foundation, and Guangdong Key Technologies for Treatment of Brain Disorders (2018B030332001) to E.X.W..