4692
Fast and Automatic Rank Determination (ARD) via Deep Learning for Low-rank Calibrationless Reconstruction1Laboratory of Biomedical Imaging and Signal Processing, The University of Hong Kong, Hong Kong, China, 2Electrical and Electronic Engineering, The University of Hong Kong, Hong Kong, China, 3Electrical and Electronic Engineering, Southern University of Science and Technology, Shenzhen, China
Synopsis
Low-rank matrix completion has emerged as a potent reconstruction approach for calibrationless parallel imaging. However, in all existing low-rank reconstruction methods, the rank threshold must be carefully chosen slice by slice in a manual and trial-and-error manner, severely hindering the adoption of low-rank reconstruction in routine clinical applications. To tackle the problem, we proposed a fast and automatic rank determination via deep learning. It directly determines optimal rank from undersampled k-space data by exploiting coil sensitivity and finite image support. Our proposed method enables fast, automatic and robust rank determination for all existing calibrationless reconstruction using low-rank matrix completion.
Introduction
Calibrationless reconstruction using low-rank matrix completion1-10 has emerged as a powerful approach for accelerated parallel imaging. During the reconstruction, rank plays an important role in precisely dividing the low-rank matrix into span subspace and null subspace6. Singular vectors (bases) of the two subspaces can be transformed into coil sensitivity and finite spatial support, dominating the low-rank approximation accuracy7,11. However, an optimal rank that differentiates span and null spaces can not be directly derived from undersampled k-space data. For all existing calibrationless reconstruction methods using low-rank matrix completion, the rank must be carefully chosen slice by slice in a manual and trial-and-error manner (it depends on both coil sensitivity and image support), severely hindering the adoption of low-rank matrix approximation methods for routine clinical applications. Here, we proposed a deep learning (DL) based fast and automatic rank determination method to estimate rank directly from undersampled data by exploring the coil sensitivity and finite image support information. Additionally, MR data acquired from the same MR coil array system share strong correlations in coil sensitivity among subjects. In this study, such correlations were further utilized as prior MR knowledge to regularize the DL model.Theory and Methods
Challenges in Rank DeterminationIn conventional low-rank reconstruction methods1-6,8-10, the recovery of undersampled k-space data is conducted by sequentially performing matrix SVD and rank thresholding on the structured low-rank matrix. As shown in Figure 1A, an optimal rank that accurately separates span subspace and null subspace can be easily determined when k-space data are fully sampled. Note that only with such optimal rank can low-rank reconstruction obtain satisfactory results (Figure 1B). However, when k-space data are undersampled, the optimal rank determination becomes challenging because the span and null subspaces are no longer differentiable (Figure 1A). To determine such optimal rank from undersampled k-space data, conventional calibrationless low-rank reconstruction methods require extensive manual fine-tuning, which is usually burdensome and computationally demanding.
Coil sensitivity and finite image support are implicitly exploited in existing low-rank reconstruction methods1-10. Specifically, the singular vectors of span subspace and null subspace can be transformed into coil sensitivity and finite image support, respectively7,9,10 (Figure 1C). As indicated in Figure 2, rank is dominated by both coil sensitivity and finite image support. Because coil sensitivity and finite image support vary between slices among subjects, it’s onerous to determine the optimal rank slice by slice. Thus, an automatic rank determination is desired.
Two-stage ResNet-based Model for Automatic Rank Determination (ARD)
As an alternative to the computationally demanding and manual search in the conventional low-reconstruction pipeline (Figure 3A), we proposed a fast ARD method. This method could be integrated with existing reconstruction methods using low-rank matrix completion to achieve a more efficient reconstruction framework (Figure 3B).
In the ARD method, a 2-stage ResNet12-based model was designed to estimate finite image support and coil sensitivity dominated rank directly from multi-channel k-space zero-padded reconstruction images, where the coil-subject geometry parameters (i.e., three angles and three translations) were incorporated as prior MR knowledge. Specifically, as shown in Figure 3C, in the first stage, the images were spatially aligned to the coil array system and then used to train a ResNet to estimate rank (RankDLalign). In the second stage, RankDLalign and multi-channel images served as multiple inputs were used to train the second ResNet to estimate rank (RankDLtarget) for subsequent reconstruction, where coil-subject geometry information from images was utilized.
Data Preparation, Training and Evaluation
Calgary-Campinas Public Data were used13. They were acquired with 12-channel coil, 3D T1-weighted GRE sequence with 1 mm isotropic resolution and matrix 256x218x100 from 61 healthy subjects (divided to 52 for training and 9 for testing). 12 channels were combined into 6 channels in our implementation14. The target ranks for training were determined using the conventional pipeline (Figure 3A). The k-space data were undersampled with random undersampling patterns (R=3). Adam optimizer was used to minimize L1 loss for two 10-layer ResNets. To evaluate the ARD performance, we integrated ARD with the existing low-rank matrix approximation methods LORAKS4 and SAKE3.
Results
Figures 4 and 5 show LORAKS and SAKE reconstruction results using rank determined by our proposed ARD. In Figure 4, four slices with distinct finite spatial supports and coil sensitivities were reconstructed using three ranks (50, 70, and 90), showing optimal rank is slice-dependent, which again demonstrates manually fine-tuning the rank threshold slice by slice is required in the conventional pipeline. The proposed ARD directly estimated optimal rank (estimation errors within 3), yielding reconstruction results comparable to those using the manually chosen optimal ranks. Figure 5 shows the proposed ARD could also be integrated with SAKE, generating reconstruction results with effectively suppressed the aliasing artifacts.Discussion and Conclusions
This study developed a DL-based fast and automatic rank determination method. Our proposed method exploited coil sensitivity and finite image support via DL, allowing optimal rank to be directly determined from undersampled k-space data. We successfully demonstrated it for LORAKS and SAKE reconstruction, and it is also expected to robustly work with other low-rank reconstruction methods such as ALOHA5 and GIRAF algorithm10. Future study can extend the proposed ARD to a more powerful 3D reconstruction.Acknowledgements
This work was supported in part by Hong Kong Research Grant Council (R7003-19F, HKU17112120 and HKU17127121 to E.X.W., and HKU17103819, HKU17104020 and HKU17127021 to A.T.L.L.), Lam Woo Foundation, and Guangdong Key Technologies for Treatment of Brain Disorders (2018B030332001) to E.X.W..References
[1] Yi Z, Liu Y, Zhao Y et al. Joint calibrationless reconstruction of highly undersampled multicontrast MR datasets using a low‐rank Hankel tensor completion framework. Magn Reson Med 2021;85(6):3256-3271.
[2] Liu Y, Yi Z, Zhao Y et al. Calibrationless parallel imaging reconstruction for multislice MR data using low‐rank tensor completion. Magn Reson Med 2021;85(2):897-911.
[3] Shin PJ, Larson PEZ, Ohliger MA et al. Calibrationless parallel imaging reconstruction based on structured low-rank matrix completion. Magn Reson Med 2014;72(4):959-970.
[4] Haldar JP. Low-Rank Modeling of Local k-Space Neighborhoods (LORAKS) for Constrained MRI. IEEE Trans Med Imaging 2014;33(3):668-681.
[5] Lee D, Jin KH, Kim EY et al. Acceleration of MR parameter mapping using annihilating filter-based low rank hankel matrix (ALOHA). Magn Reson Med 2016;76(6):1848-1864.
[6] Zhang J, Liu C, Moseley ME. Parallel reconstruction using null operations: Parallel Imaging Reconstruction. Magn Reson Med 2011;66(5):1241-1253.
[7] Yi Z, Zhao Z, Liu Y et al. Fast Calibrationless Image-space Reconstruction by Structured Low-rank Tensor Estimation of Coil Sensitivity and Spatial Support. In: Proceedings of the 29th Annual Meeting of ISMRM, 2021, p 0067.
[8] Haldar JP, Setsompop K. Linear Predictability in Magnetic Resonance Imaging Reconstruction: Leveraging Shift-Invariant Fourier Structure for Faster and Better Imaging. IEEE Signal Processing Magazine 2020;37(1):69-82.
[9] Haldar JP, Zhuo J. P-LORAKS: Low-rank modeling of local k-space neighborhoods with parallel imaging data. Magn Reson Med 2016;75(4):1499-1514.
[10] Ongie G, Jacob M. A Fast Algorithm for Convolutional Structured Low-Rank Matrix Recovery. IEEE Transactions on Computational Imaging 2017;3(4):535-550.
[11] Uecker M, Lai P, Murphy MJ et al. ESPIRiT-an eigenvalue approach to autocalibrating parallel MRI: where SENSE meets GRAPPA. Magn Reson Med 2014;71(3):990-1001.
[12] He, K., Zhang, X., Ren, S. et al. Deep residual learning for image recognition. IEEE Conference on Computer Vision and Pattern Recognition 2016;770-778.
[13] Souza R, Lucena O, Garrafa J et al. An open, multi-vendor, multi-field-strength brain MR dataset and analysis of publicly available skull stripping methods agreement. Neuroimage 2018;170:482-494.
[14] Buehrer M, Pruessmann KP, Boesiger P et al. Array compression for MRI with large coil arrays. Magn Reson Med. 2007;57(6):1131-9.
Figures
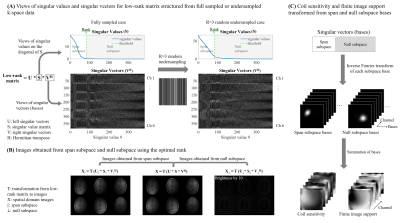
Figure 1. (A) Views of singular values and singular vectors for low-rank matrix structured from full sampled or undersampled k-space data. The optimal rank (green line) divides the structured low-rank matrix (along with its singular values and singular vectors) into span and null subspace. (B) Images obtained from span subspace and null subspace using the optimal rank. Note that only with an optimal rank can the low-rank reconstruction obtain satisfactory results. (C) Coil sensitivity and finite image support transformed from span and null subspace bases.
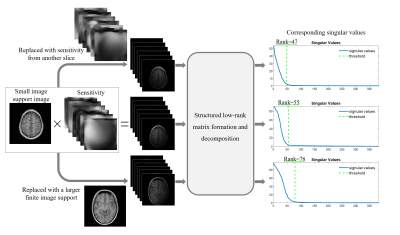
Figure 2. Coil sensitivity and finite image support dependent optimal rank determination. Coil sensitivity and finite image support from original data were replaced to simulate their influences on optimal rank determination. The results show the optimal rank increased by around 35% when a larger image support was applied, or reduced by around 15% when coil sensitivity from another slice was applied, indicating the optimal rank could vary among different slices or subjects, thus leading conventional manual rank determination to be burdensome and computationally demanding.
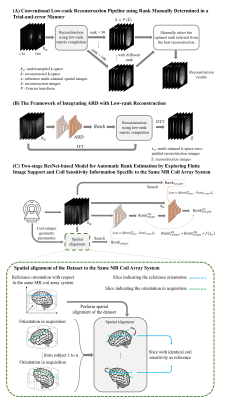
Figure 3. (A) Conventional low-rank reconstruction pipeline using rank manually determined in a trial-and-error manner. (B) The framework of integrating ARD with low-rank reconstruction, where rank was automatically determined from multi-channel zero-padded reconstruction images. (C) Two-stage ResNet-based model for automatic rank estimation by exploring finite image support and coil sensitivity information specific to the same MR coil array system.
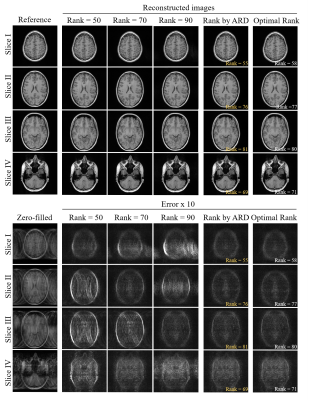
Figure 4. LORAKS reconstruction results using the rank automatically determined by the proposed ARD. The reconstruction showed improved results, in terms of effectively suppressed artifacts, when compared to those using manually determined rank (i.e., ranks = 50, 70 and 90 for four slices with different finite spatial support and sensitivity). The proposed ARD directly estimated optimal rank (estimation errors within 3), yielding reconstruction results comparable to those using the manually chosen optimal ranks.
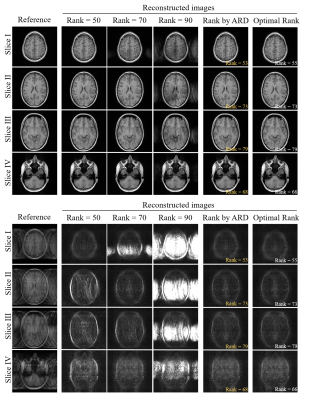
Figure 5. SAKE reconstruction results using the rank automatically determined by the proposed ARD. The reconstruction showed more significant artifact suppression when compared to those using manually determined rank (i.e., ranks = 50, 70 and 90 for four slices with different finite spatial support and sensitivity). Using the proposed ARD integrated with SAKE, the reconstruction results were also comparable to those using the manually chosen optimal ranks, demonstrating the robustness of our method.