4690
Cascaded hybrid k-space and image generative adversarial network for fast MRI reconstruction1School of Biomedical Engineering, ShanghaiTech University, Shanghai, China
Synopsis
A cascaded hybrid domain generative adversarial network is proposed for accelerated MRI reconstruction. A novel multi-scale feature fusion sampling layer is proposed to replace the pooling layers and upsampling layers in the U-Net k-space generator to better recover the missing samplings. The proposed method is extensively validated with low and high acceleration factors against several state-of-the-art reconstruction methods, and achieves competitive reconstruction performance.
Introduction
MRI is known to have low acquisition speed, and acceleration is essential to reduce acquisition times. Parallel imaging1 and compressed sensing2 have achieved significant progress in fast MRI, but the achievable acceleration is still limited. Deep learning-based MRI reconstruction methods have been proposed to further increase the acceleration factors and improve the reconstruction quality, including the standalone denoising network and the unrolled cascade networks4-11. More recently, a powerful generative adversarial neural network (GAN) is proposed to use both k-space and image generators to recover undersampling k-space, and has achieved superior performance compared with existing state-of-the-art deep learning reconstruction methods3. However, this method used the same U-Net architecture for the k-space and image generators, while the simple pooling and upsampling layers in the k-space U-Net may be suboptimal for k-space recovery. Moreover, the existing hybrid-domain GAN method works like a denoising network without data consistency5 (DC) enforcement.In this work, we propose a novel unrolled hybrid-domain GAN reconstruction network, where the k-space generator architecture is specifically optimized to better recover the missing samples and the DC is enforced during unrolling optimization.
Methods
Reconstruction frameworkThe proposed Cascaded Hybrid Domain Generative Adversarial Network (CHD-GAN) is shown in Fig. 1, which consists of k-space generator (G-K), image generator (G-I), data consistency layers and discriminator. The G-K takes input of the undersampled k-space, where noise is added to the zero entries and outputs the reconstructed k-space. The reconstructed missing points are merged with the input samples and inputted to G-K after inverse Fourier transform for further image refinement. The k-space and image generators use the U-Net architecture as the backbone. However, considering that the G-K plays an import role in recovering the missing information, we propose to replace the pooling and up-sampling layers in the G-K U-Net with a novel multi-scale feature fusion sampling layer (MSFS, detailed in Fig. 2 ), which extracts multi-scale k-space information to better recover the missing samplings. The cascaded k-space and image generators are then put into an unrolled optimization framework, where the generative networks perform denoising and recover the missing information followed by DC enforcement. We adopt similar discriminator to the previous GAN-based reconstruction network3, the input to which is the fully sampled grund truth image or the reconstructed image, and the output of which forms adversarial loss.
Loss function
The loss function to train the CHD-GAN includes the k-space loss ($$$Loss_k^n$$$), the image space loss ($$$Loss_I^n$$$) and the adversarial discriminator loss ($$$Loss_D$$$). We define $$$y$$$ as fully-sampled k-space, $$$y_z$$$ as noise-filled k-space, $$$F_u$$$ as Fourier transform, ε as the complex noise, $$$M$$$ as the sampling mask, and $$$N=1−M$$$ as mask for points not sampled. n(n= 1,2) is the number of the unrolled iteration. $$$y_I^n$$$ is the input of the nth G-K, and $$$x_I^n$$$ is the input data of the nth G-I:
$$y_I^0 = y_z =M⊗y + N⊗ε$$
$$x_I^n = F_u^H(G_K^n(y^n_I)⊗ M+M⊗y)$$
$$y_I^n = (F_u G_I^{n-1} x_I^{n-1}) ⊗ M + M ⊗ y$$
The k-space loss calculates the mean-squared-error between the G-K output and the fully sampled k-space: $$Loss_k^n = ||G_K^n(y_I^n) - y||_2^2$$
The image space loss consists of L1 loss, L2 loss and the gradient difference loss between the G-I output and the fully sampled image: $$Loss_I^n =||G_I^n(x_I^n) - F_u^H y||_2^2 + ||G_I^n(x_I^n) - F_u^H y||_1^2 +||\nabla(F_u^H y)-\nabla(G_I^n(x_I^n))||_2^2$$ The total geneator loss is the weighted combinaiton of loss at each iteration: $$Loss_G^n = Loss_k^n + Loss_I^n$$ $$Loss_{G_{all}} = \sum_{n=0}^m e^{n-m} ⊗ Loss_G^n$$
Commonly used cross entropy loss is adopted for $$$Loss_D$$$. Therefore, the total network loss can be defined as: $$Loss_{total} = Loss_{G_{all}} + Loss_D$$
Dataset and evaluation
The human brain dataset contains 78 volumetric brain MR images. A total of 3120 T1-weighted images with matrix size of 256x256 are used to evaluate the reconstruction performance, with randomly selected 2400 slices for training and 720 slices for testing.
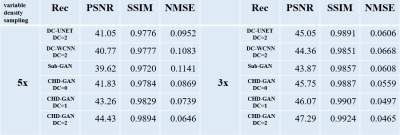
Increasing the number of unrolling iterations of CHD-GAN will increase the computational cost, while our initial experiments indicate that the reconstruction improvement is not obvious when the iteration number exceeds 2. Peak Signal-to-Noise Ratio (PSNR), Structural Similarity Index (SSIM) and Normalized Mean Square Error (NMSE) are calculated to evaluate the reconstruction performance in comparsion with several state-of-the-art deep-learning reconstructions for 3x and 5x variable density undersampling.
Results
Example reconstruction results of the 6 reconstruction methods for 3x and 5x variable density undersampling as well as the fully sampled reference is shown in Fig. 3. The proposed the CHD-GAN performs the best by recovering fine structures. Table 1 provides the PSNR, SSIM and NMSE of all investigative reconstruction methods, and CHD-GAN consistently performs the best for all undersampling factors. Especially, CHD-GAN without unrolling still outperforms the previous hybrid-domain GAN, indicating the proposed MSFS layer contributes to the reconstruction performance improvement.Discussion & Conclusion
We develop a cascaded hybrid domain generative adversarial network for accelerated MRI reconstruction. A novel multi-scale feature fusion sampling layer is proposed to replace the pooling layers and upsampling layers in the k-space generator to better recover the missing samplings. The proposed method is extensively validated with different acceleration factors against several state-of-the-art reconstruction methods, and achieves competitive reconstruction performance. The proposed method will be validated in real acquired undersampled data.Acknowledgements
No acknowledgement found.References
1. Mark A Griswold, Peter M Jakob, Robin M Heide-mann, Mathias Nittka, Vladimir Jellus, Jianmin Wang,Berthold Kiefer, and Axel Haase, “Generalized autocal-ibrating partially parallel acquisitions (grappa),”Mag-netic Resonance in Medicine: An Official Journal ofthe International Society for Magnetic Resonance inMedicine, vol. 47, no. 6, pp. 1202–1210, 2002.
2. Michael Lustig, David Donoho, and John M Pauly,“Sparse mri: The application of compressed sensing forrapid mr imaging,”Magnetic Resonance in Medicine:An Official Journal of the International Society for Mag-netic Resonance in Medicine, vol. 58, no. 6, pp. 1182–1195, 2007.
3. Roy Shaul, Itamar David, Ohad Shitrit, and Tammy Rik-lin Raviv,“Subsampled brain mri reconstruction bygenerative adversarial neural networks,”Medical ImageAnalysis, vol. 65, pp. 101747, 2020.
4. Shanshan Wang, Zhenghang Su, Leslie Ying, Xi Peng,Shun Zhu, Feng Liang, Dagan Feng, and Dong Liang,“Accelerating magnetic resonance imaging via deeplearning,” in2016 IEEE 13th international symposiumon biomedical imaging (ISBI). IEEE, 2016, pp. 514–517.
5. Jo Schlemper, Jose Caballero, Joseph V Hajnal, An-thony N Price, and Daniel Rueckert, “A deep cascadeof convolutional neural networks for dynamic mr imagereconstruction,”IEEE transactions on Medical Imaging,vol. 37, no. 2, pp. 491–503, 2017.
6. Yan Yang, Jian Sun, Huibin Li, and Zongben Xu,“Admm-csnet: A deep learning approach for imagecompressive sensing,”IEEE transactions on patternanalysis and machine intelligence, vol. 42, no. 3, pp.521–538, 2018.
7. Simiao Yu, Hao Dong, Guang Yang, Greg Slabaugh,Pier Luigi Dragotti, Xujiong Ye, Fangde Liu, Simon Ar-ridge, Jennifer Keegan, David Firmin, et al., “Deepde-aliasing for fast compressive sensing mri,”arXivpreprint arXiv:1705.07137, 2017.
8. Morteza Mardani, Enhao Gong, Joseph Y Cheng,Shreyas Vasanawala, Greg Zaharchuk, Marcus Alley,Neil Thakur, Song Han, William Dally, John M Pauly,et al.,“Deep generative adversarial networks forcompressed sensing automates mri,”arXiv preprintarXiv:1706.00051, 2017.
9. Hao Zheng, Faming Fang, and Guixu Zhang, “Cascadeddilated dense network with two-step data consistency formri reconstruction,” 2019.
10. Sriprabha Ramanarayanan, Balamurali Murugesan,Keerthi Ram, and Mohanasankar Sivaprakasam, “Dc-wcnn: A deep cascade of wavelet based convolutionalneural networks for mr image reconstruction,”in2020 IEEE 17th International Symposium on Biomed-ical Imaging (ISBI). IEEE, 2020, pp. 1069–1073.
11. Liyan Sun, Zhiwen Fan, Xinghao Ding, Yue Huang, andJohn Paisley, “Joint cs-mri reconstruction and segmen-tation with a unified deep network,” in Information Pro-cessing in Medical Imaging, 2019, pp. 492–504.
Figures
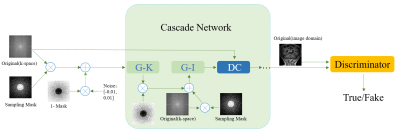
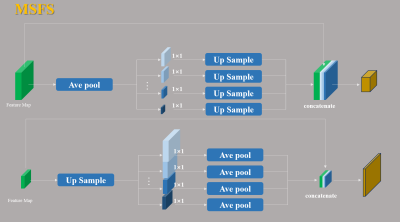
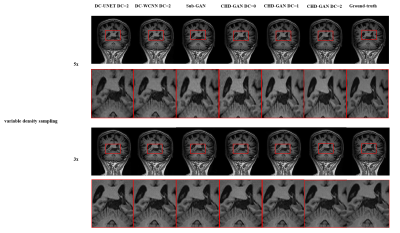
Fig. 3. Example reconstruction results of the 6 reconstruction methods for 3x and 5x variable density undersampling as well as the fully sampled reference. DC-UNET11 and DC-WCNN10 have two unrolled iterations. Sub-GAN3 is the previous hybrid-domain GAN.