Introduction

We have witnessed a significant surge of interest in using deep learning (DL) for image reconstruction. Existing DL frameworks used in MR image reconstructions are more or less based on those designed for computer vision tasks^1,2, which usually have millions of training data and solve relatively simpler learning problems (i.e., pattern recognition)³. In contrast, for most MR image reconstruction tasks, only limited training data are available⁴, which can lead to instability problems^5,6. As a result, direct DL-based reconstructions are often sensitive to changes in data acquisition parameters encountered in practice⁵. In this work, we proposed a novel method to address this problem. Specifically, we exploited the fact that MR images of a specific organ (e.g., the brain) often reside in a low-dimensional subspace and the subspace structure (or, basis functions) can be determined from limited training data. With pre-learned basis functions, the subspace model can be determined robustly from limited k-space data acquired using different sampling patterns. To compensate for the limitation in representation power of a subspace model, we trained a DL network to learn a mapping from a linear vector space to a nonlinear manifold. The synergistic integration of a subspace model with a DL network significantly improves the reconstruction performance compared to each component used individually. The proposed method has been evaluated using the fastMRI dataset⁷, producing significantly improved reconstructions over the state-of-the-art DL-based method.

Methods

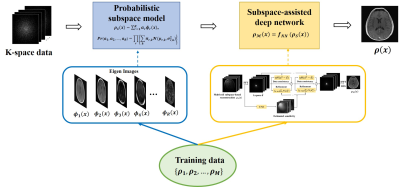
The proposed method consists of two main components: a probabilistic subspace model and a DL network as illustrated in Fig. 1.

Probabilistic subspace model
Subspace models have been used extensively to capture low-rank structures in high-dimensional image functions for constrained image reconstruction^8,9. Here we extend this approach further by using a probabilistic subspace model to capture the statistical distribution of training data and then to obtain an initial reconstruction that is optimal in terms of maximum-a-posteriori (MAP). Specifically, we represent each of the training images as:$$\rho_{S}(x)=\sum_{r=1}^Ra_{r}\phi_{r}(x),\hspace{20em}(1)$$where the basis functions, $$$\small\left\{\phi_{r}(x)\right\}$$$, can be obtained as the eigen images of the training data $$$\small\left\{\rho_{1},\rho_{2},...,\rho_{M}\right\}$$$ by performing principal component analysis¹⁰. With this model, we can estimate $$$\small P(\rho)$$$ in a very low-dimensional setting. More specifically, we treat $$$\small\left\{a_{r}\right\}$$$ (instead of each pixel) as random variables and each training image as a draw from $$$\small P(a_{1},a_{2},...,a_{R})$$$. We further treat $$$\small a_{1},a_{2},...,a_{R}$$$ as independent such that $$$\small P(a_{1},a_{2},...,a_{R})=P(a_{1})P(a_{2})...P(a_{R})$$$. Note that $$$\small P(a_{1})P(a_{2})...P(a_{R})$$$ is the maximum entropy approximation of $$$\small P(a_{1},a_{2},...,a_{R})$$$ given the set of the observations $$$\small\left\{a_{1,m}\ ,a_{2,m}\ ,...,a_{R,m}\right\}_{m=1}^M$$$ derived from the training data. The probability distribution function as estimated is, therefore, least restrictive (or informative) as a constraint given the training data while the basis functions play a significant role in capturing the global dependence of the image features in the training data. With this model, subspace-based reconstruction from a new data set can be obtained as:
$$\left\{\hat{a}_r\right\}=\arg\min_\left\{a_r\right\}\frac{1}{2}||d-E(\sum_{r=1}^Ra_{r}\phi_{r}(x))||_2^{2}-\sigma_n^2\log(P(\left\{a_r\right\})),\hspace{4em}(2)$$ where $$$\small d$$$ denotes the measured data, $$$\small E$$$ the imaging operator and $$$\small\sigma_n^2$$$ the variance of the measurement noise.

Subspace-assisted manifold learning
While the linear vector space model can be learned easily and represent the training data well, it does not capture all the prior information in $$$\small\left\{\rho_{1},\rho_{2},...,\rho_{M}\right\}$$$. In other words, given the learning outcomes: $$$\small\left\{\phi_{r}(x)\right\}_{r=1}^R$$$ and $$$\small P(a_{1},a_{2},...,a_{R})$$$, $$$\small\left\{\rho_{1},\rho_{2},...,\rho_{M}\right\}$$$ cannot be reproduced by statistical sampling. In addition, if new images contain features outside the span of $$$\small\left\{\phi_{1}(x),\phi_{2}(x),...,\phi_{R}(x)\right\}$$$, these features will be lost. Here, we propose to integrate subspace model learning with deep learning to take advantages of their complementary strengths while avoiding their respective weaknesses. More specifically, we use a DL network to learn a mapping from the subspace representation to the true image:$$\hat{\rho}_{M}(x)=f_{NN}(\hat{\rho}_{S}(x)).\hspace{20em}(3)$$ Many network architectures can be utilized for this task. We adapted the state-of-the-art end-to-end variational network (E2E-VN)¹¹.

Experimental Results

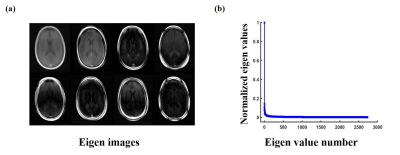
We evaluated the performance of the proposed method using multi-coil T1POST brain images from the fastMRI dataset. Total 910 subjects were included for training and 110 subjects for validation. The data were retrospectively under-sampled using a Gaussian random sampling pattern with variable density (R=8). The reconstructions from the fully sampled k-space data were used as the ground truth.

Figure 2 shows the learned eigen images and corresponding eigen values from our training dataset. The rapid decay of the eigne values validates the proposed subspace representation.

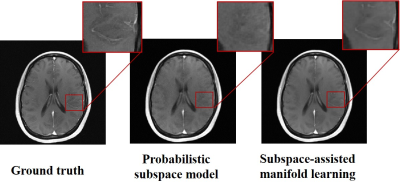
Figure 3 demonstrates that subspace-assisted manifold learning can recover the features lost in the reconstruction obtained using the subspace model alone.

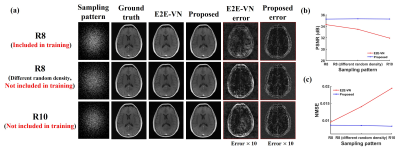
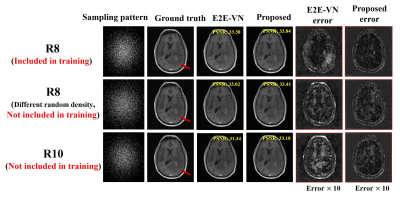
Figure 4 compares the robustness of the proposed method with E2E-VN against data acquisition changes. As can be seen, the proposed method produced more accurate and robust reconstructions in all the scenarios tested.

Figure 5 shows the reconstructions obtained by E2E-VN and the proposed method from data with lesion. As can be seen, the proposed method not only better recovered the normal and lesion features, but also produced more stable results for different sampling patterns.

Conclusion

We presented a new method to capture prior information in a training set for constrained image reconstruction. The proposed method synergistically integrates subspace learning with deep learning, significantly improving the reconstruction performance compared to each component used alone. This proposed method may provide an effective means to enhance the robustness and practical utility of deep learning-based image reconstruction.

Acknowledgements

This work was supported in a part by National Natural Science Foundation of China (62001293).