4688

A Deep Unrolled Network for Reconstruction of Real-time Interventional MRI with Multi-coil Radial Sampling

Zhao He¹, Ya-Nan Zhu², Yuchen He², Yu Chen¹, Suhao Qiu¹, Linghan Kong¹, Xiaoqun Zhang², and Yuan Feng¹
¹School of Biomedical Engineering, Shanghai Jiao Tong University, Shanghai, China, ²School of Mathematical Sciences, MOE-LSC and Institute of Natural Sciences, Shanghai Jiao Tong University, Shanghai, China

Synopsis

Interventional MRI (i-MRI) needs fast data acquisition and image reconstruction. We have shown that a Low-rank and Sparsity decomposition with Framelet transform model with Primal dual fixed point optimization (LSFP) could satisfy the reconstruction of real-time i-MRI. In this study, we unrolled the LSFP into a deep neural network, dubbed LSFP-Net, with multi-coil golden-angle radial sampling. Simulation results showed that LSFP-Net outperformed the state-of-the-art methods, and a phantom experiment demonstrated its potential for real-time i-MRI.

Introduction

Image guidance with interventional MRI (i-MRI) could greatly improve the accuracy and outcomes of neurosurgery ^1,2. To accelerate MRI, many model-based algorithms have been proposed ^3-5, such as Low-rank plus Sparse decomposition (L+S) ⁶ or k-t Robust Principal Component Analysis (k-t RPCA) ⁷. However, the long computation time for iterations makes these methods difficult to achieve real-time imaging. Recently, deep learning-based algorithms have been proposed for fast MRI ^8,9, such as CRNN ^10,11, ISTA-Net ¹², and L+S-Net ¹³. However, most of these methods reconstruct MR images in a retrospective scheme after all data acquisition. We have shown that LSFP could satisfy the requirements of real-time i-MRI ¹⁴, but parameter tuning is still challenging. Here to further reduce the computation cost and address the parameter tuning problem, we proposed a deep unrolled network, dubbed LSFP-Net, for real-time i-MRI reconstruction. A group-based reconstruction scheme with multi-coil golden-angle radial sampling was used. A set of brain intervention images were simulated for training and testing. An interventional experiment with LSFP-Net for reconstruction was implemented to demonstrate its potential for real-time i-MRI.

Methods

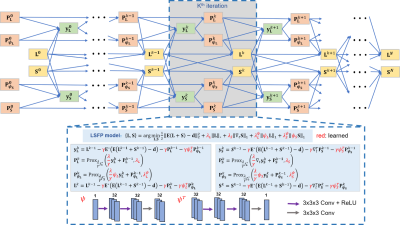
To accelerate i-MRI, we have proposed a Low-rank and Sparsity decomposition with Framelet transform (LSF) model ¹⁴: $$\left \{ \textbf{L}, \textbf{S} \right \} = \textrm{arg } \underset{\textbf{L}, \textbf{S}}{\mathrm{\boldsymbol{}min}}\frac{1}{2}\left \| \textbf{E}(\textbf{L}+\textbf{S})-\textbf{d}) \right \|_{2}^{2}+\lambda _{L}\left \| \textbf{L} \right \|_{*}+\lambda _{S}\left \| \bigtriangledown_{t} \textbf{S} \right \|_{1}+\lambda _{\textrm{L}}^{\psi}\left \| \psi \textbf{L} \right \|_{1}+\lambda _{S}^{\psi }\left \| \psi \textbf{S} \right \|_{1}, \qquad \qquad (1)$$ where image sequence is separated into a low-rank component $$$\textbf{L}$$$ and a sparse component $$$\textbf{S}$$$. The problem (1) optimized with a primal dual fixed point method was named LSFP ¹⁴.
However, parameter tuning and long iteration time limit the application of LSFP in real-time i-MRI. Therefore, we proposed a deep unrolled network, dubbed LSFP-Net (Figure 1). This network unrolls the iteration steps of the LSFP algorithm into several iteration blocks. The regularization parameters and sparse transforms are learnable. The spatial sparse transforms $$$\psi$$$ and $$$\psi ^{T}$$$ are designed as a combination of 3D convolutional operators and rectified linear unit (ReLU).
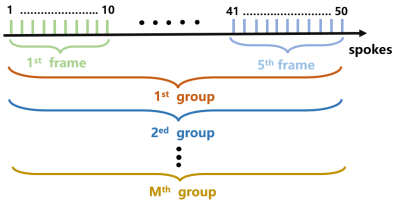
To achieve real-time i-MRI, we applied a group-based reconstruction scheme with multi-coil golden-angle radial sampling (Figure 2). Interventional images are reconstructed in a group-wise way. Specifically, in this study, only 10 spokes per frame and 5 frames per group were used for reconstruction.
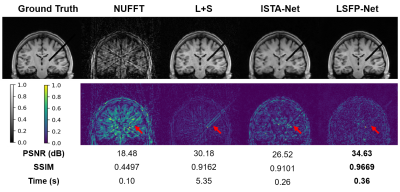
To evaluate the performance of LSPP-Net, a set of brain interventional images was simulated for training and testing. The fully sampled brain MR images from 10 healthy subjects were collected on a 3T MRI scanner (uMR 790, United Imaging Healthcare, Shanghai, China). For each subject, 8 coronal slices were acquired with a matrix size of 128 x 128 and 11 channels. Four different intervention setups (2 unilateral and 2 bilateral) for each slice were simulated. The training data includes 9600 simulated interventional MR images from 8 volunteers. The testing dataset consists of 2400 images from another 2 volunteers. The reconstruction results from LSFP-Net were compared with those from Nonuniform Fast Fourier Transform (NUFFT), L+S, and ISTA-Net.
Furthermore, an interventional experiment with a gelatin phantom was carried out. The interventional images were reconstructed with LSFP-Net in real-time. The following sequence parameters were used: FOV=300x300 (mm²), acquisition matrix=256x256, slice thickness=5mm, channels=17, and TR/TE=3.56ms/1.9ms. The model was implemented with Pytorch on an Ubuntu 20.04 LTS (64-bit) operating system equipped with an AMD Ryzen 9 5950x central processing unit (CPU) and NVIDIA RTX 3090 graphics processing unit (GPU, 24 GB memory).

Results

Simulation results showed that LSFP-Net performed better than NUFFT, L+S, and ISTA-Net with 5 frames per group and 10 spokes per frame (Figure 3). In addition, LSFP-Net could reconstruct the interventional features better with a reconstruction time of 0.36s. Phantom experiment results showed that the position of the interventional needle could be well reconstructed using LSFP-Net, with a temporal resolution of 0.16s/frame (Figure 4).

Conclusion

We proposed a deep unrolled network, dubbed LSFP-Net, for real-time i-MRI reconstruction with multi-coil golden-angle radial sampling. Simulation results showed that LSFP-Net outperformed the state-of-the-art methods, and a phantom experiment demonstrated its potential for real-time i-MRI.

Acknowledgements

Funding support from grant 31870941 from National Natural Science Foundation of China (NSFC) and grant 19441907700 from Science and Technology Commission of Shanghai Municipality (STCSM) are acknowledged.

References

1. He X, Liu M, Liu C, Fang J, Xu Y, Wang L, Xiang J, Sequeiros RB, Li C. Real-time MR-guided brain biopsy using 1.0-T open MRI scanner. Eur Radiol 2019;29(1):85-92.

2. Lee PS, Richardson RM. Interventional MRI-Guided Deep Brain Stimulation Lead Implantation. Neurosurg Clin N Am 2017;28(4):535-544. 3. Lustig M, Donoho D, Medicine JMPJMRi. Sparse MRI: The application of compressed sensing for rapid MR imaging. 2007;58(6).

4. Yang AC, Kretzler M, Sudarski S, Gulani V, Seiberlich N. Sparse Reconstruction Techniques in Magnetic Resonance Imaging: Methods, Applications, and Challenges to Clinical Adoption. Invest Radiol 2016;51(6):349-364.

5. Sandino CM, Cheng JY, Chen F, Mardani M, Pauly JM, Vasanawala SS. Compressed Sensing: From Research to Clinical Practice with Deep Neural Networks. IEEE Signal Process Mag 2020;37(1):111-127.

6. Otazo R, Candes E, Sodickson DK. Low-rank plus sparse matrix decomposition for accelerated dynamic MRI with separation of background and dynamic components. Magn Reson Med 2015;73(3):1125-1136.

7. Tremoulheac B, Dikaios N, Atkinson D, Arridge SR. Dynamic MR Image Reconstruction-Separation From Undersampled (k, t)-Space via Low-Rank Plus Sparse Prior. IEEE Trans Med Imaging 2014;33(8):1689-1701.

8. Liang D, Cheng J, Ke Z, Ying L. Deep Magnetic Resonance Image Reconstruction: Inverse Problems Meet Neural Networks. Ieee Signal Processing Magazine 2020;37(1):141-151.

9. Wang S, Xiao T, Liu Q, Zheng H. Deep learning for fast MR imaging: A review for learning reconstruction from incomplete k-space data. Biomedical Signal Processing and Control 2021;68.

10. Qin C, Schlemper J, Caballero J, Price AN, Hajnal JV, Rueckert D. Convolutional Recurrent Neural Networks for Dynamic MR Image Reconstruction. IEEE Trans Med Imaging 2019;38(1):280-290.

11. Zhang Y, She H, Du YP. Dynamic MRI of the abdomen using parallel non-Cartesian convolutional recurrent neural networks. Magn Reson Med 2021.

12. Zhang J, Ghanem B. ISTA-Net: Interpretable Optimization-Inspired Deep Network for Image Compressive Sensing. 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition2018. p 1828-1837.

13. Huang W, Ke Z, Cui ZX, Cheng J, Qiu Z, Jia S, Ying L, Zhu Y, Liang D. Deep low-Rank plus sparse network for dynamic MR imaging. Med Image Anal 2021;73:102190.

14. He Z, Zhu Y-N, Qiu S, Zhang X, Feng Y. Low-Rank and Framelet Based Sparsity Decomposition for Interventional MRI Reconstruction. 2021. p arXiv:2107.11947.

Figures

Figure 1. The proposed LSFP-Net architecture. LSFP-Net is composed of N blocks, and each block strictly corresponds to one iteration in the LSFP algorithm. The spatial sparse transforms $$$\psi$$$ and $$$\psi ^{T}$$$ are designed as a combination of 3D convolutional operators and rectified linear unit (ReLU). The learnable parameters and sparse transforms are marked in red.

Figure 2. Illustration of the group-based reconstruction scheme with multi-coil golden-angle radial sampling. Interventional images are reconstructed in a group-wise way. Each frame only uses limited k-space data acquired with multi-coil golden-angle radial sampling. The radial spokes in k-space were acquired continuously with a golden-angle format in one group, but the overall sampling trajectory was kept consistent among different groups.

Figure 3. A comparison of simulated intervention between different algorithms. Reconstruction was carried out using 5 frames per group and 10 spokes per frame (matrix size=128x128, acceleration factor 20) The red arrows indicate the interventional features.

Figure 4. Intervention of a gel phantom. Reconstruction was carried out using 5 frames per group and 10 spokes per frame (matrix size =256x256, acceleration factor 40) by LSFP-Net. The yellow arrows indicate the interventional needle tips.

Proc. Intl. Soc. Mag. Reson. Med. 30 (2022)

4688

DOI: https://doi.org/10.58530/2022/4688