4687
Low-Rank Shot-phase Estimation for Multi-shot DWI Reconstruction1Department of Electronic Science, Biomedical Intelligent Cloud R&D Center, Fujian Provincial Key Laboratory of Plasma and Magnetic Resonance, National Institute for Data Science in Health and Medicine, Xiamen University, Xiamen, China, 2School of Computer and Information Engineering, Xiamen University of Technology, Xiamen, China, 3United Imaging Healthcare, Shanghai, China
Synopsis
Diffusion-weighted imaging (DWI) is widely employed in clinical diagnosis and white matter connections mapping. Multi-shot interleaved echo planer imaging (ms-iEPI) is used for acquiring images with higher spatial resolution and fewer distortion but suffers from motion-induced shot-phase variations. In this work, a joint reconstruction model is proposed to obtain the shot-phase and composite magnitude image simultaneously. Specifically, the smoothness of the shot-phase is exploited to construct low-rank constraints. Experiment results show that the proposed method has better performance than state-of-the-art methods on shot-phase estimation and image reconstruction.
Purpose
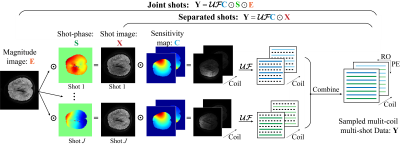
DWI is a noninvasive tool for water molecules diffusion modelling [1]. Ms-iEPI has become increasingly popular for higher spatial resolution and less distortion DWI images [2]. However, motion-induced shot-phase variations result in ghosting artefacts [3]. Navigator echo can measure shot-phase variations but increase scan time and can be mismatched with image echo sometimes [4]. As shown in Figure 1, navigator-free methods can be separated into two kinds: PLRHM [5] and MUSSELS [4] reconstruct each shot image separately by low-rank matrix completion approaches. MUSE[6] and POCS-ICE[7] try to obtain the shot-phase and a composite magnitude image. In this work, we propose a navigator-free method falling in the second kind. The rank of structured matrix lifted from each shot data is constrained for smooth shot-phase estimation.Methods
The proposed reconstruction model with smooth shot-phase estimation is shown in model (1). The data consistency is designed to follow a joint shots procedure to reconstruct a composite magnitude image with all sampled shots, as shown in Figure 1. The structured matrices are constructed as a regularizer item by lifting k-space sampled data. Assuming that the shot-phase is smooth and has tight support in k-space, the structured matrix will be low-rank[5, 8, 9]. Thus, the smooth shot-phase can be solved by constraining the rank of the structured matrices.$$
\begin{equation}
\mathop{\min}_{\boldsymbol{\rm S_{\textit{j}},E}} {\frac{\lambda}{2}}{\sum_{j=1}^{J}}{\sum_{i=1}^{I}}{\lVert \boldsymbol {\rm Y_{\textit{ij}}} - {\mathcal{UF}\boldsymbol{\rm C_{\textit{i}}\odot S_{\textit j}\odot E}} \rVert}_{\rm F}^{2}+{\sum_{j=1}^{J} \lVert {\mathcal{PF} \boldsymbol{\rm S_{\textit j}\odot E}} \rVert_{*}},
\tag{1}
\end{equation}
$$
where the $$$\boldsymbol{\rm{Y}_{\textit{ij}}} \in {\mathbb{C}^{N_x \times N_y}}$$$ denotes i-th coil and j-th shot sampled k-space data, $$$\boldsymbol{\rm C_{\textit{i}}}$$$ is the i-th coil sensitivity map, $$$\boldsymbol{\rm S_{\textit{j}}}$$$ is the j-th shot-phase, which is updated within the iterative solving steps. $$$\boldsymbol{\rm{E}} \in {\mathbb{C}^{N_x \times N_y}}$$$ is the target composite magnitude image, $$$I$$$ is the number of coils and $$$J$$$ is the number of shots, $$$\mathcal{U}$$$ is an under-sampling operator, $$$\mathcal{F}$$$ is the Fourier transform operator, $$$\mathcal{P}$$$ is an operator to build structured matrix[5], $$$\lambda$$$ is a regularization parameter, $$$\lVert {\cdot}\rVert _{\rm F}$$$ represents Frobenius norm, $$$\lVert {\cdot}\rVert _{*}$$$ denotes nuclear norm, $$$\odot$$$ means Hadamard product.
we adopt the Projections Onto Convex Sets algorithm to solve the proposed model[10]. The solution $$$\boldsymbol{\rm{E}}$$$ can be considered to lie in a closed convex subset in a Hilbert space. Two convex sets defined by data consistency and regularizer items have a non-empty intersection [10]. Each point in this intersection is a potential solution for model (1). The image reconstruction problem can be solved by building a projection operator for each convex set [11]. In the iterative solving process, the shot-phase is estimated from intermediate images with smoothness constraints.
Results
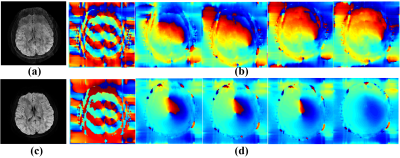
The brain dataset with navigator echo obtained on a Philips 3T Achieva TX scanner is used in experiments: coil = 8, shot = 8, TE/TR = 77/3000ms, FOV = 23×23cm2, matrix size = 236×232, diffusion directions = 15, b-values = 800 s/mm2, slice thickness = 4 mm, number of signal averages = 1, lines of navigator along phase encoding direction = 17. Coil sensitivity maps are calculated by ESPIRIT using non-diffusion images (b-value equals zero) [12]. Average angular error (AAE) [4] is taken as an objective criterion to quantify the reconstruction. The lower AAE indicates the reconstructed DWI images have better motion artefacts removed. Three navigator-free state-of-the-art methods including POCS-ICE [7], MUSSELS [4], and PLRHM [5] are used for comparison. A navigator-based method IRIS is used for reference [13].Figure 2 compares estimated shot-phases in the iterative solving process. POCS-ICE fails to get smooth shot-phase and motion-induced ghosting artefacts still exists in the final magnitude image. Conversely, the estimated shot-phase of the proposed method becomes increasingly smooth and finally leads to a reconstructed image without ghosting artefacts. The result demonstrates that the low-rank constraint could facilitate the shot-phase estimation and magnitude image reconstruction.
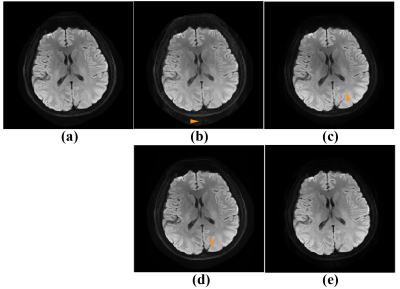
Figure 3 shows the averaged DWI image of 15 diffusion directions. Obvious ghosting artefacts have been marked with yellow arrows in Figure 3 (b)-(d). The 8-coil 8-shot data is challenging for the separated shots reconstruction methods, which try to obtain each shot image following a parallel imaging procedure. The proposed method outperforms other state-of-the-art methods visually.
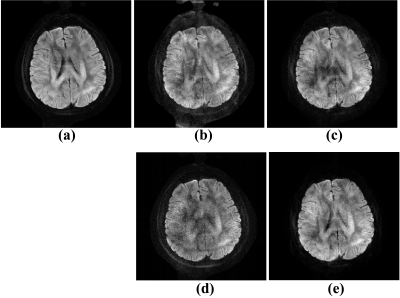
Furthermore, we test algorithm performance on under-sampled reconstruction. Figure 4 shows the proposed method has better robustness on under-sampled data. It demonstrates that the joint shots strategy reduces the scale of unknowns which decrease the difficulty of solving this underdetermined equation.
The proposed method has been extended with a weighted total variation to increase the signal to noise ratio. See more details and results in the full-length paper: https://csrc.xmu.edu.cn/.
Conclusion
In this work, we propose a joint low-rank shot-phase estimation method for reconstructing high spatial resolution and less distorted ms-iEPI DWI images. We believe that it is of great significance for the further applications of ms-shot iEPI DWI in clinical diagnosis and human brain function research.Acknowledgements
This work was supported in part by the National Natural Science Foundation of China under grants 62122064, 61971361, 61871341, and 61811530021, the National Key R&D Program of China under grant 2017YFC0108703, and the Xiamen University Nanqiang Outstanding Talents Program. The authors thank Hua Guo for assisting in data acquisition and very helpful advice for the abstract. The authors thank Lijun Bao, Weibin Zhou and Zunquan Chen for the discussion on fractional anisotropy maps.
The correspondence should be sent to Prof. Xiaobo Qu (Email: quxiaobo@xmu.edu.cn)
References
[1] D. K. Jones et al., ''Diffusion MRI,'' Oxford University Press, 2010.
[2] M. A. Bernstein et al., ''Handbook of MRI pulse sequences,'' Elsevier, 2004.
[3] A. W. Anderson et al., ''Analysis and correction of motion artifacts in diffusion weighted imaging,'' Magnetic Resonance in Medicine, vol. 32, pp. 379-87, 1994.
[4] M. Mani et al., ''Multi‐shot sensitivity‐encoded diffusion data recovery using structured low‐rank matrix completion (MUSSELS),'' Magnetic Resonance in Medicine, vol. 78, pp. 494-507, 2017.
[5] Y. Huang et al., ''Phase-constrained reconstruction of high-resolution multi-shot diffusion weighted image,'' Journal of Magnetic Resonance, vol. 312, pp. 106690, 2020.
[6] N.-k. Chen et al., ''A robust multi-shot scan strategy for high-resolution diffusion weighted MRI enabled by multiplexed sensitivity-encoding (MUSE),'' Neuroimage, vol. 72, pp. 41-47, 2013.
[7] H. Guo et al., ''POCS‐enhanced inherent correction of motion‐induced phase errors (POCS‐ICE) for high‐resolution multishot diffusion MRI,'' Magnetic Resonance in Medicine, vol. 75, pp. 169-180, 2016. [8] X. Zhang et al., ''Image reconstruction with low-rankness and self-consistency of k-space data in parallel MRI,'' Medical Image Analysis, vol. 63, pp. 101687, 2020.
[9] J. P. Haldar, ''Low-rank modeling of local k -space neighborhoods (LORAKS) for constrained MRI,'' IEEE Transactions on Medical Imaging, vol. 33, pp. 668-681, 2013.
[10] A. A. Samsonov et al., ''POCSENSE: POCS-based reconstruction for sensitivity encoded magnetic resonance imaging,'' Magnetic Resonance in Medicine, vol. 52, pp. 1397-1406, 2004.
[11] M. L. Chu et al., ''POCS-based reconstruction of multiplexed sensitivity encoded MRI (POCSMUSE): A general algorithm for reducing motion-related artifacts,'' Magnetic Resonance in Medicine, vol. 74, pp. 1336-48, 2015.
[12] M. Uecker et al., ''ESPIRiT—an eigenvalue approach to autocalibrating parallel MRI: where SENSE meets GRAPPA,'' Magnetic Resonance in Medicine, vol. 71, pp. 990-1001, 2014.
[13] H.-K. Jeong et al., ''High-resolution human diffusion tensor imaging using 2-D navigated multishot SENSE EPI at 7 T,'' Magnetic Resonance in Medicine, vol. 69, pp. 793-802, 2013.
Figures