4684
Boosting of Half-Quadratic Splitting Algorithm for Undersampled Brain MRI Reconstruction
Qingyong Zhu1, Jing Cheng2, Zhuo-Xu Cui1, Yuanyuan Liu3, Yanjie Zhu2, and Dong Liang1
1Research Center for Medical AI, SIAT, Chinese Academy of Sciences, Shenzhen, China, 2Paul C. Lauterbur Research Center for Biomedical Imaging, SIAT, Chinese Academy of Sciences, Shenzhen, China, 3National Innovation Center for Advanced Medical Devices, Shenzhen, China, Shenzhen, China
1Research Center for Medical AI, SIAT, Chinese Academy of Sciences, Shenzhen, China, 2Paul C. Lauterbur Research Center for Biomedical Imaging, SIAT, Chinese Academy of Sciences, Shenzhen, China, 3National Innovation Center for Advanced Medical Devices, Shenzhen, China, Shenzhen, China
Synopsis
The existing accelerated MRI methods have the limitations such as fine-structure loss in the cases of high reduction factors or noisy measurements. This work presents a novel mutual-structure filtering based half-quadratic splitting algorithm for accurate undersampled brain MRI reconstruction. Experimental results on in-vivo images have shown that the proposed approach has a superior ability to capture meaningful details compared with other state-of-the-art reference guided reconstruction technologies.
Introduction
With proper discretization, the reconstruction system for accelearted brain MRI using sparse sampling can be commonly modeled as,\begin{equation}b=\mathcal{A}x+\zeta\end{equation}where $$$x\in\mathbb{C}^{N\times1}$$$ is the target image, and $$$b\in\mathbb{C}^{M\times1}$$$ is $$$k$$$-space data. $$$\mathcal{A}\in\mathbb{C}^{M\times N}(M\ll N)$$$ is the undersampled Fourier encoding matrix. $$$\zeta\in\mathbb{C}^{M\times1}$$$ is observed noise supposed to be complex Gaussian. Our goal is to recover $$$x$$$ form $$$b$$$ by solving the under-determined problem. By adding the image prior $$$\textit{p}(x)\propto \exp\left(-\mathcal{R}(x)\right)$$$, the variational formulation for this under-determined problem can be written as:\begin{equation}\mathop{\arg\min}_{x\in\mathbb{C}^{N\times1}}\frac{1}{2}\!\parallel\!\mathcal{A}x-b\!\parallel_{2}^{2}+\lambda \phi(x)\end{equation}where $$$\lambda\in R_{+}$$$ is regularization parameter. Both data fidelity term and regularizing term are usually complicated nonlinear or nonsmooth function, which is not advisable to simply apply the gradient descent optimization. A half-quadratic splitting (HQS) algorithm1 is used to decouple the above problem,\begin{align}&u=\mathop{\arg\min}_{x\in\mathbb{C}^{N\times1}}\frac{1}{2}\!\parallel\!\mathcal{A}x-b\!\parallel_2^2+\frac{\mu}{2}\!\!\parallel\!x-g\!\parallel_2^2\\ &g=\mathop{\arg\min}_{g\in\mathbb{C}^{N\times1}}\frac{\mu}{2}\parallel\!g-u\!\parallel_2^2+\lambda\phi(g)\end{align}where the second sub-problem is uaually the proximal operator of the regularization $$$\phi(g)$$$, and it can reduce to the additive white gaussian noise (AWGN) based plug-and-play filtering of the updated $$$u$$$, deriving a class of boosting algorithms in HQS framework.
Method
Here we propose a boosting scheme of HQS algorithm based on mutual-structure filtering2, whose formulations are, \begin{align*} u&=\mathop{\arg\min}_{x\in\mathbb{C}^{N\times1}}\frac{1}{2}\!\parallel\!\mathcal{A}x-b\!\parallel_2^2+\frac{\mu}{2}\sum_{n}\!\!\parallel\!x_{n}-g_{n}\!\parallel_2^2\\ g_{n}&=w_{n}^{1-\rm{SSIM}}\cdot{\mathcal{M}}_{n}\left(u\right) + w_{n}^{\rm{SSIM}} \cdot{\mathcal{M}}_{n}\left({\mathcal{F}}\left(u,x_{r}\right)\right),~~n=1,2\end{align*}where the reference guided mutual filtering $$${\mathcal{F}}$$$ takes the common structures contained in both images to avoid transferring unwanted structures from the reference image to target image, which is with three terms,\begin{equation}\mathop{\arg\min}_{u,x_{r},a,b}E_{S}(u,x_{r},a,b)+E_{d}(u,x_{r})+E_{r}(a,b)\end{equation}with\begin{align*}E_{S}(u,x_{r},a,b)=&\!\!\!\!\sum_{q\in N(p)}\left(\left(a_{p}^1u_{q}+a_{p}^{0}-x_{r,q}\right)^2+\left(b_{p}^1x_{r,q}+b_{p}^{0}-u_{q}\right)^2\right)\\E_{d}(u,x_{r})=&\sum_{p}\lambda\parallel x_{r,p}-x_{r,p}^{0}\parallel_{2}^{2} + \beta\parallel u_{p}-{u_{p}}^{0}\parallel_{2}^{2} \\E_{r}(a,b)=&\sum_{p}(\xi_{1}(a_{p}^{1})^{2}+\xi_{2}(b_{p}^{1})^{2})\end{align*}The $$$E_{S}$$$ is the structure similarity term based on the patch-level analysis, which can be defined as a least square regression function of local patches centered at $$$p$$$. The $$$a$$$ and $$$b$$$ are the regression coefficient sets. Considering circumventing trivial solution, another constraint $$$E_{d}$$$ based on Euclidean norm is utilized. The $$$E_{r}$$$ is introduced to smoothing with strength of $$$\xi_{1}$$$ and $$$\xi_{2}$$$. The scale operator $$${\mathcal M}_{n}$$$ applies a low-pass filter $$$\mathcal{H}$$$ followed by down-sampling $$$\mathcal{D}$$$. The $$$w_{n}^{\rm{SSIM}}$$$ based on structure similarity (SSIM)3 is expressed as,\begin{align} w_{n}^{\rm{SSIM}} &=|c(p,q)s(p,q)|=\frac{2\sigma_p\sigma_q+C_1}{\sigma_p^2+\sigma_q^2+C_1}|\frac{\sigma_{pq}+C_2}{\sigma_p\sigma_q+C_2}| \nonumber=|\frac{2\sigma_{pq}+C_1}{\sigma_p^2+\sigma_q^2+C_1}|\nonumber\\ w_{n}^{\rm{1-SSIM}} &=1-|c(p,q)s(p,q)|=1-|\frac{2\sigma_{pq}+C_1}{\sigma_p^2+\sigma_q^2+C_1}|\nonumber \end{align}where $$$p$$$ and $$$q$$$ denote two local image patches, the contrast variation $$$c(p,q)$$$ which calculates the reduction of contrast variation of $$$\mathcal{M}_{n}\left({\mathcal{F}}\left(u,x_{r}\right)\right)$$$ due to the Gaussian degraded operation $$$G$$$, and the correlation $$$s(p,q)$$$ which quantifies the structural correction between $$$\mathcal{M}_{n}\left({\mathcal{F}}\left(u,x_{r}\right)\right)$$$ and $$$G\left(\mathcal{M}_{n}\left({\mathcal{F}}\left(u,x_{r}\right)\right)\right)$$$. The local statistics $$$\mu_p$$$, $$$\sigma_p$$$ and $$$\sigma_{pq}$$$ are defined as $$$\mu_p=\sum_{i=1}^N p_i$$$, $$$\sigma_p=(\sum_{i=1}^{N}(p_i-\mu_p)^2)^{1/2}$$$ and $$$\sigma_{pq}=\sum_{i=1}^{N}(p_i-\mu_p)(q_i-\mu_q)$$$. The constants $$$C_1$$$ and $$$C_2=C_1/2$$$ are introduced for numerical stability. For each element in $$$w_{n}^{1-\rm{SSIM}}(0\leq w_{n}^{\rm{1-SSIM}}\leq 1)$$$, the more its value is close to 1, the higher probability it belongs to the structure part. The weighting scheme enables to obtain the prior image $$$g_{n}$$$ with good edge defining.Results
We evaluated the performance of the proposed method on multi-contrast brain MR images and 1D variable density random undersampling pattern is adopted to generate sampled k-space data. A pre-acquired proton-density (PD) weighted image (TR=5000 ms, TE=9.7 ms) as a reference to reconstruct a subsequently scanned T1 weighted image (TR=2000 ms, TE=9.7 ms) using a turbo spin echo sequence (Matrix size=384$$$\times$$$324, FOV=230$$$\times$$$187 mm$$$^{2}$$$, slice thickness=5.0 mm). Two state-of-the-art reference guided compressed sensing MRI methods based on location prior (CS-wTV)4 and orientation prior (CS-GOP)5 were conducted for comparison. We can obviously observe that severe aliasing artifacts occur in the CS-wTV reconstructions at reduction factor of R=4 and 5. With reference guided orientation incorporated, the artifacts in images are alleviated but still obvious and unacceptable. As expected, the proposed technique provides considerable promising results that the aliasing artifacts are significantly suppressed and more fine details are efficiently preserved even at reduction factor R=5. The corresponding quantitative values of all the reconstructed images of the three methods under different reduction factors are given in Table.1. The proposed method always outperforms the other methods in term of the RLNE and PSNR criteria, and its RT is also comparable to other methods.Conclusion
In this work, a novel reference guided accelerated MRI reconstruction approach based on half-quadratic splitting algorithm has been introduced for accurate brain MRI reconstruction from undersampled $$$k$$$-space data. Experimental results have shown that the proposed method shows the significant advantage over other two state-of-the-art reference guided CS-MRI reconstruction methods.Acknowledgements
This work was supported in part by the National Key R&D Program of China (2017YFC0108802 and 2017YFC0112903); National Natural Science Foundation of China (61771463, 81830056, U1805261, 81971611, 61871373, 81729003, 81901736); Natural Science Foundation of Guangdong Province (2018A0303130132); Key Laboratory for Magnetic Resonance and Multimodality Imaging of Guangdong Province; Shenzhen Peacock Plan Team Program (KQTD20180413181834876); Innovation and Technology Commission of the government of Hong Kong SAR (MRP/001/18X); Strategic Priority Research Program of Chinese Academy of Sciences (XDB25000000).References
- Mila N and Michael K N. Analysis of half-quadratic minimization methods for signal and image recovery. SIAM J. Scientific Comput. 2005; 27(3):937–966.
- Shen X Y, Zhou C, Xu L, et al. Mutual-Structure for Joint Filtering. 2015 IEEE Int. Conf. on Computer Vision (ICCV). 2015.
- Wang Z, Bovik, A. C., Sheikh, H. R., et al. Image quality assess-ment: from error visibility to structural similarity. IEEE Trans. ImageProcess. 2004; 13: 600-612.
- Haldar J P, Hernando D, Song S K, et al. Anatomically con-strained reconstruction from noisy data. Magn. Reson. Med. 2008; 59(4): 810-818.
- Peng X, Zhu Q. Y, Wang S S, et al. Reference guided CS-MRI with gradient orientation priors. 2015 IEEE Int. Conf. in Medicineand Biology Society (EMBS). 2015.
Figures
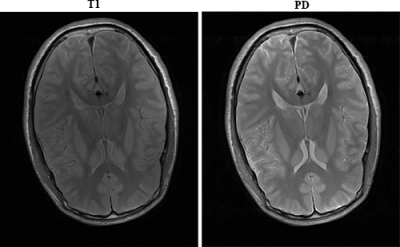
Figure.1 T1-weighted image and PD-weighted image.
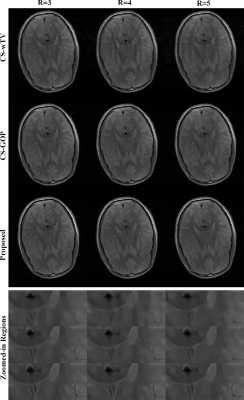
Figure.2 T1-weighted image and PD-weighted image.Figure.2 Reconstruction results of CS-wTV, CS-GOP and the proposed method using 1D under-sampling pattern at reduction factors of R=3, 4 and 5. The corresponding local regions of returned images are enlarged for better visualization.

Table.1 The quantitative comparisons of various reconstructions on different reduction factors. The running time (RT) is measured to evaluate the algorithm efficiency. The reconstruction quality is quantified with the relative \unboldmath $$${\textit{l}_{2}}$$$-norm error (RLNE) and peak signal to noise ratio (PSNR).
DOI: https://doi.org/10.58530/2022/4684