4683
Densely-overlapped locally low-rank algorithms outperform conventional locally low-rank algorithms for accelerating parametric mapping1Shanghai Jiao Tong University, Xuhui, China, 2Yale University, New Haven, CT, United States
Synopsis
The Locally Low-Rank (LLR) constraint has been increasingly used for MR acceleration. Here we compare two strategies for LLR-constrained reconstruction, namely the Non-overlapped LLR (NLLR) and the Densely-overlapped LLR (DLLR) to show their differences. The NLLR strategy has been used by a number of LLR algorithms, including the most well-known POCS algorithm. On the other hand, the DLLR strategy has not been well-recognized as a different strategy, and algorithms able to employ the strategy have only been developed recently. In this work, we show that DLLR is different and superior to NLLR by yielding faster convergence and reduced undersampling artifacts.
Introduction
The Locally Low-Rank (LLR) constraint has been increasingly used for acceleration of MR parametric mapping(1). In many recent works(1-4), a Non-overlapped LLR (NLLR) enforcement strategy, which enforces LLR over a randomly selected subset of non-overlapped blocks in each iteration, was employed to facilitate efficient computation. A notable work along this line is the LLR-POCS algorithm, which is combined with POCS-SPIRiT(5) to further improve the acceleration rate. On the other hand, densely enforcing LLR over every blocks (DLLR) in every iteration is possible with a recently proposed LLR algorithm based on Alternating Direction Method of Multipliers (ADMM), although the work(6) was not aimed to distinguish DLLR from the previous NLLR strategy. To date, whether there is a difference of performance between NLLR and DLLR, two strategies of LLR-constrained reconstruction, remains unclear and unexplored. In this work, we show that DLLR is different and superior to NLLR by yielding faster convergence, reduced undersampling artifacts, and improved numerical stability when ADMM and POCS are respectively used.Methods
The technical details for the NLLR-POCS and DLLR-ADMM algorithms can be found in the original papers(1,6). Here the two algorithms were performed and compared to accelerate brain and cardiac T2 mapping. All subjects provided written informed consent. Brain T2 mapping was performed by T2-weighted TSE with 8 different TEs (14-180ms) in one healthy subject (male, age 25) in a 3T scanner (uMR790, United Imaging Healthcare, Shanghai, China) with a 32-channel head coil. Other parameters were: TR/ETL/FOV/matrix size/slice thickness/echo spacing/bandwidth= 1000ms/13/260mm×260mm/256×256/5mm/13.82ms/130 Hz/pixel. Cardiac T2-prep bSSFP T2 mapping(7) with 4 effective TEs (0ms, 24ms, 44ms, and 64ms) was performed in 10 healthy subjects (3 male, age 31±8) in a 3T scanner (Siemens Trio, Erlangen, Germany) with a 24-channel spine coil and 18-channel torso coil, firstly by full sampling and then prospective undersampling. Retrospective undersampling was based on uniform interleaved Cartesian undersampling(8) and variable-density pseudorandom undersampling(9), while prospective undersampling was based on uniform interleaved Cartesian undersampling(8). Image resolution was 2.3mm×3.2mm and 1.4mm×1.4mm for the retrospectively and prospectively accelerated imaging, respectively. Other parameters were: FOV/slice thickness/bandwidth/TR/flip angle/acceleration rate= 360mm×270mm/8mm/1495 Hz/pixel/2.4ms/40°/4.An LLR block size of 5×1 was used since the undersampling was only along the phase-encoding direction. For DLLR-ADMM, coil maps were separately generated by the adaptive method(10) and ESPIRiT(11) for retrospective and prospective acceleration, respectively. NLLR-POCS was executed with either 30 iterations following the convention (NLLR-POCS-30), or with 300 iterations (NLLR-POCS-300) to fully reveal its performance.
Results
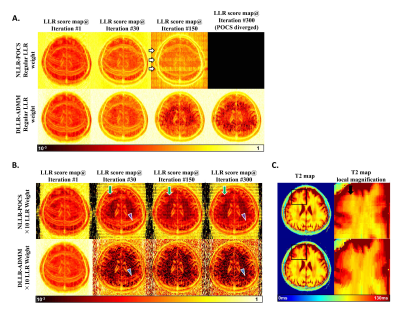
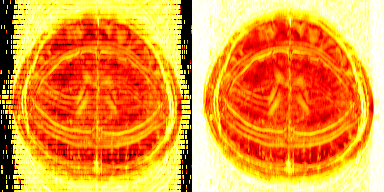
Figure 1 shows the reconstruction of T2 and spin density maps in the brain based on NLLR-POCS-30 and DLLR-ADMM with 8-fold uniform or pseudorandom undersampling. DLLR-ADMM showed clear improvement of image quality compared with NLLR-POCS, including less aliasing artifacts and reduced blurring.Figures 2 shows the LLR score map (a block-by-block evaluation of Nucleus norm of the Casorati matrix) at Iteration #1, #30, #150, and #300 of the two algorithms for two LLR weights. A higher LLR score indicated less stringent LLR enforcement and insufficient convergence. In Panel A, the DLLR-ADMM algorithm led to a gradual decrease of the LLR score and, as a result, the artifact attenuation. The NLLR-POCS algorithm, however, not only failed to attenuate the aliasing artifacts, but also gradually diverged after 30 iterations, which was found attributable to error accumulation in the SPIRiT self-consistency equation. On the other hand, when the LLR weight was upscaled by 10-fold, NLLR-POCS started to show an alternated LLR enforcement between different subsets of non-overlapped blocks (Panel B), which led to blocky artifacts as shown in Panel C. Figure 3 shows an animation recording the dynamic variation of LLR scores in the first 30 iterations. One can clearly see the jittered convergence in the DLLR-POCS algorithm.
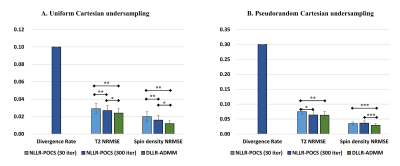
Figure 4 shows the statistical comparison of the two algorithms in the cardiac T2 mapping with 10 healthy subjects. DLLR-ADMM achieved significantly improved NRMSE compared with NLLR-POCS with 30 or 300 iterations, with a stronger improvement observed for uniform undersampling, where artifacts tend to be stronger (cf. Figure 1). NLLR-POCS-300 also caused divergence in 10-30% of subjects depending on the undersampling strategy adopted.
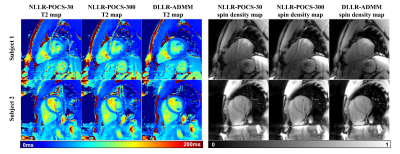
Figure 5 shows comparison of NLLR-POCS-30, NLLR-POCS-300, and DLLR-ADMM with prospective uniform undersampling of k-space in two healthy subjects. DLLR-ADMM showed clear improvement of mapping quality in both T2 and spin density maps.
Discussion and conclusions
Our results indicated that NLLR generates a slower convergence than DLLR due to the jittering of LLR enforcement between different subsets of blocks. This jittering occurred possibly because LLR enforcement in one block would inherently cause degeneration of LLR property in its neighboring blocks since the two blocks are overlapped. Thus, each iteration of the NLLR enforcement was somewhat undoing the work performed by the previous iterations, causing sluggish convergence. The instability issue associated with POCS-SPIRiT was reported before(5) and further impaired the performance of NLLR-POCS. The reconstruction time of DLLR-ADMM was comparable with NLLR, since the ADMM algorithm considerably simplified the formulation(6). In conclusion, despite the common use of NLLR in the past literature, our results suggest that DLLR may lead to faster convergence and improved quality for LLR-regularized reconstruction.Acknowledgements
No acknowledgement found.References
1. Zhang T, Pauly JM, Levesque IR. Accelerating parameter mapping with a locally low rank constraint. Magn Reson Med 2015;73(2):655-661.
2. Lugauer F, Nickel D, Wetzl J, Kiefer B, Hornegger J, Maier A. Accelerating multi-echo water-fat MRI with a joint locally low-rank and spatial sparsity-promoting reconstruction. Magnetic Resonance Materials in Physics, Biology and Medicine 2017;30(2):189-202.
3. Liu Y, Ying L, Chen W, Cui Z-X, Zhu Q, Liu X, Zheng H, Liang D, Zhu Y. Accelerating the 3D T(1ρ) mapping of cartilage using a signal-compensated robust tensor principal component analysis model. Quant Imaging Med Surg 2021;11(8):3376-3391.
4. Hu Y, Wang X, Tian Q, Yang G, Daniel B, McNab J, Hargreaves B. Multi-shot diffusion-weighted MRI reconstruction with magnitude-based spatial-angular locally low-rank regularization (SPA-LLR). Magn Reson Med 2020;83(5):1596-1607.
5. Lustig M, Pauly JM. SPIRiT: Iterative self-consistent parallel imaging reconstruction from arbitrary k-space. Magnetic Resonance in Medicine 2010;64(2):457-471.
6. Lima da Cruz G, Bustin A, Jaubert O, Schneider T, Botnar RM, Prieto C. Sparsity and locally low rank regularization for MR fingerprinting. Magnetic Resonance in Medicine 2019;81(6):3530-3543.
7. Giri S, Chung YC, Merchant A, Mihai G, Rajagopalan S, Raman SV, Simonetti OP. T2 quantification for improved detection of myocardial edema. J Cardiovasc Magn Reson 2009;11:56.
8. Hu C, Peters DC. SUPER: A blockwise curve-fitting method for accelerating MR parametric mapping with fast reconstruction. Magn Reson Med 2019;81(6):3515-3529.
9. Lustig M, Donoho D, Pauly JM. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magn Reson Med 2007;58.
10. Griswold MA, Walsh D, Heidemann R, Haase A, Jakob P. The Use of an Adaptive Reconstruction for Array Coil Sensitivity Mapping and Intensity Normalization. 2002. p 2410.
11. Uecker M, Lai P, Murphy MJ, Virtue P, Elad M, Pauly JM, Vasanawala SS, Lustig M. ESPIRiT--an eigenvalue approach to autocalibrating parallel MRI: where SENSE meets GRAPPA. Magn Reson Med 2014;71(3):990-1001.
Figures
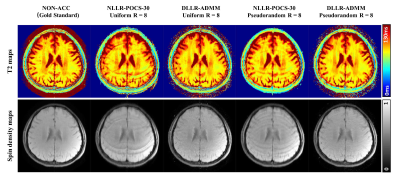
Figure 1. The reconstruction of T2 and spin density maps in the brain based on NLLR-POCS-30 and DLLR-ADMM with 8-fold uniform or pseudorandom undersampling. DLLR-ADMM showed clear improvement of image quality compared with NLLR-POCS, including less aliasing artifacts and reduced blurring.