Introduction

The past few years have seen a surge of interest in using deep learning-based methods to reconstruct T2 maps from highly sparse imaging data.^1-5 A practical challenge for deep learning-based T2 mapping lies in the lack of multi-TE experimental data with ground truth required for network training. An effective method was recently proposed to address this issue, which involves the use of single-TE image priors, as well as generalized series (GS) and sparse modeling.⁶ This work extends this method by integrating GS modeling with deep learning (DL). This novel integration exploits the complementary information provided by the GS model and deep network to substantially improve the reconstruction quality. In addition, the proposed method enables the use of synthetic data for network training because the deep network was trained only to compensate the GS model. The proposed method has been validated using experimental data, producing more accurate brain T2 maps as compared with the state-of-the-art methods.

Method

Following our recent study,⁶ we decomposed the desired image functions of different TEs as:
$$\rho(\boldsymbol{x}, t)=\sum_{m=-M}^{M} \alpha_{m}(t) \rho_{\mathrm{ref}}(\boldsymbol{x}, t) e^{-i 2 \pi m \Delta \boldsymbol{k} \cdot \boldsymbol{x}}+\rho_{\mathrm{s}}(\boldsymbol{x}, t)$$
where $$$t=\mathrm{TE}_{1}, \mathrm{TE}_{2}, \ldots, \mathrm{TE}_{n}$$$;$$$\rho_{\text {ref }}(\boldsymbol{x}, t)$$$ represents the GS reference image for absorbing the anatomical information;$$$\rho_{\mathrm{s}}(\boldsymbol{x}, t)$$$ denotes the sparse component for capturing subject-dependent novel features. In previous study, $$$\rho_{\text {ref }}(\boldsymbol{x}, t)$$$ was obtained using a deep learning-based image translation scheme that generated reference images for different TEs from the companion T1-weighted image and $$$\rho_{\mathrm{s}}(\boldsymbol{x}, t)$$$ was determined by solving an $$$L_{1}$$$ norm-based compressed sensing reconstruction problem.

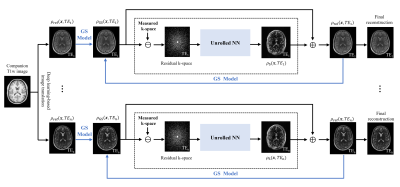
In this work, we further generalized this reconstruction framework by synergistically integrating GS modeling with deep learning. The proposed method has three novel features to improve reconstruction performance. First, instead of using a hand-crafted sparsity-promoting regularizer for $$$\rho_{\mathrm{s}}(\boldsymbol{x}, t)$$$, we learned its optimal functional form through an unrolled network. This data-driven regularizer has been demonstrated to be more effective in constraining the recovery of image features.^7-10Second, instead of fixing $$$\rho_{\text {ref }}(\boldsymbol{x}, t)$$$, we iteratively updated them by including the recovered novel features produced by the network. In this way, the deep network only serves to compensate the spatial basis functions in the GS model, and consequently, it can be trained using simulated data. This feature is especially desirable for T2 mapping where only a small number of multi-TE training data are currently available. Finally, we included the output of the GS reconstruction into the deep network as a conditional prior to improve its accuracy and robustness. The overall pipeline of the proposed method is shown in Figure 1.

Specifically, in the first iteration, we generated $$$\rho_{\text {ref }}(\boldsymbol{x}, t)$$$ and determined the GS component $$$\hat{\rho}_{\mathrm{GS}}(\boldsymbol{x}, t)$$$ as was done in⁶. Then, we used a deep network to reconstruct $$$\rho_{\mathrm{s}}(\boldsymbol{x}, t)$$$ which unrolled the gradient descent algorithm for solving the following reconstruction problem:
$$\hat{\rho}_{\mathrm{s}}=\arg \min _{\rho_{\mathrm{s}}} \frac{1}{2}\left\|d-F_{\Omega}\left(\hat{\rho}_{\mathrm{GS}}+\rho_{\mathrm{s}}\right)\right\|^{2}+R\left(\rho_{\mathrm{s}} ; \hat{\rho}_{\mathrm{GS}}\right)$$
As described in⁷, this unrolled network equivalently learned the optimal regularized functional $$$R(\cdot)$$$ for recovery of $$$\hat{\rho}_{\mathrm{s}}$$$. Note differently from⁷, we conditioned the network input on $$$\hat{\rho}_{\mathrm{GS}}$$$ so that the prior information therein was incorporated to further improve and stabilize the network. Synthetic data were used to train the network, which were generated by transferring the T2-weighted images of Human Connectome Project¹¹ to T2-weighted images for different TEs through histogram matching.
After $$$\hat{\rho}_{\mathrm{S}}(\boldsymbol{x}, t)$$$ was determined, we updated the reference image as $$$\rho_{\mathrm{ref}}(\boldsymbol{x}, t)=\hat{\rho}_{\mathrm{GS}}(\boldsymbol{x}, t)+\hat{\rho}_{\mathrm{s}}(\boldsymbol{x}, t)$$$ and generated a set of new spatial basis functions for the GS model. The updated spatial bases matched better with the data, thus making the GS model-based reconstruction more accurate and the corresponding residual feature sparser. As a result, the unrolled network more effectively used the imaging data for signal recovery. By alternatively updating the GS model and unrolled network until convergence, we obtained the final reconstruction.

Results

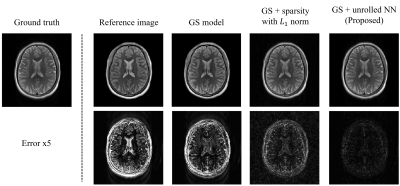
The proposed method was evaluated using experimental data obtained from the hospital.

Figure 2 shows the role of the GS model and the unrolled NN in producing the final reconstruction. As can be seen, the low-frequency discrepancies between the reference image and the ground truth were compensated by the GS model. The sparse image features were further recovered by the unrolled NN. Compared to handcrafted sparse constraints, the learned regularization term better recovered the sparse image features.

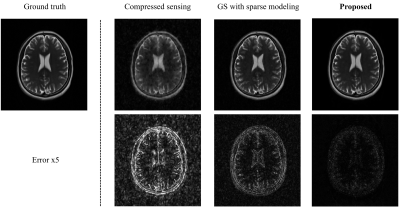
Figure 3 compares the reconstructed T2-weighted images using the proposed method with those from two existing state-of-the-art methods. As shown, the proposed method produced significantly improved results.

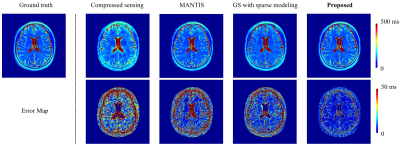
Figure 4 compares the accuracy of the T2 maps obtained using the proposed method with those of three existing state-of-the-art methods. Again, the proposed method produced much better T2 maps.

Figure 5 shows a comparison of the proposed method with three state-of-the-art methods in recovering T2 maps from data acquired from a patient. As can be seen, the proposed method was able to detect the lesion clearly.

Conclusions

We presented a new method to reconstruct brain T2 maps from highly sparse imaging data. The proposed method synergistically integrates GS modeling with deep learning for substantially improved reconstruction accuracy. Experimental results demonstrate its superior performance over state-of-the-art methods. Our method may prove useful for various MRI studies that involve quantitative T2 mapping.

Acknowledgements

No acknowledgement found.