Introduction

Non-Cartesian trajectories such as radial acquisition are used in various MRI applications due to their higher signal-to-noise ratio, shorter acquisition time, and less sensitivity to movement and flow. For radially acquired data, re-gridding is quite efficient for a given large number of spokes. However, with a low number of spokes required for accelerated data acquisition, it is subject to severe streaking artifacts originating from interpolation in the spatial frequency domain (k-space). It was recently demonstrated that for reconstruction of the 2D radial acquisition a polar algorithm, based on Hankel transform, is more robust against undersampling[1], [2]. This study extends the polar approach to 3D reconstruction of Koosh-ball acquisitions. We proposed a mathematical algorithm to directly reconstruct three-dimensional radial data (Koosh-ball) in the spherical coordinates without any frequency interpolation. In this work, the theory of this algorithm is explained, and the results of the proposed algorithm on simulated and actual 3-D radial data are presented as proof of concept.

Material and Methods

The image in the spherical coordinates system is related to this data with the following equation:
$$I(r,φ_r,θ_r)=\frac{1}{(2π)^3}\int_{0}^{2π} \int_{0}^{π} \int_{0}^{+∞} K(ρ,φ_ω,θ_ω)\exp(jω ⃗.r ⃗)ρ^2 sinφ_ω dρdφ_ω dθ_ω [1]$$
Similar to any other function in the spherical coordinates, the k-space can be expanded by using spherical harmonics as follows[3]:
$$ K(ω ⃗ )=K(ρ,φ_ω,θ_ω )=∑_{l=0}^{+∞}∑_{m=-l}^lk_l^m (ρ) Y_l^m (φ_ω,θ_ω ) [2]$$
where $$$ Y_l^m $$$ represents a spherical harmonic of degree $$$ l $$$ and order $$$ m $$$ and $$$ k_l^m (ρ) $$$ represents the frequency Fourier series coefficients that are calculated from the following equation:
$$k_l^m (ρ)= ∫_0^{2π}∫_0^πK(ρ,φ_ω,θ_ω )\overline{Y_l^m (φ_ω,θ_ω )} sinφ_ω dφ_ω dθ_ω [3]$$
The image can also be expanded based on spherical harmonics in the spherical coordinates in the form of the following equation:
$$I(r ⃗ )=I(r,φ_r,θ_r)=∑_{l=0}^{+∞}∑_{m=-l}^lI_l^m (r)Y_l^m (φ_r,θ_r) [4]$$
Where $$$I_l^m (r)$$$ is the spatial Fourier series coefficients of the final image $$$ I(r,φ_r,θ_r) $$$. These coeffiecents can then be calculated from the inverse spherical Henkel transform according to the following equation:
$$I_l^m (r)=i^l/4π S_l^{-1} (k_l^m (ρ)) [5]$$
where $$$S_l$$$ denotes the spherical Henkel transform.
In our approach, the Fourier series coefficients in the spatial frequency domain $$$(k_l^m (ρ)) $$$ are computed based on Eq.(3), and then using Eq.(5), the spatial Fourier series coefficients $$$(I_l^m (r)) $$$ are calculated, resulting in the image in the spherical coordinates with a limited number of spokes. It is worth noting that the Fourier series coefficients can be calculated to the user-defined upper limit value, e.g., L. Finally, to visualize the images in the Cartesian coordinates system, we used nearest-neighbor interpolation in the relatively smooth space domain.
We artificially simulated a 3D Koosh-ball trajectory on the 3D Shepp-Logan and brain digital phantoms to test the proposed algorithm[4]. Additionally, the MR human in vivo data was acquired on a 16 channel coil 3T Siemens scanner with a 3D Koosh-ball trajectory and 30036 spokes with 198 samples on each spoke.

Results

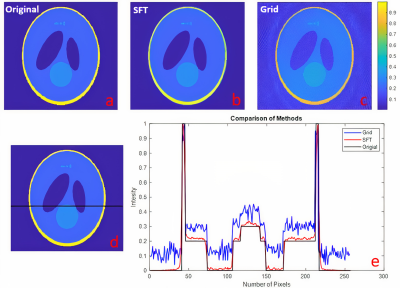
Simulated Study: The simulated data were reconstructed by the spherical Fourier transform for the spherical harmonics degree of L=90. Figures 1(a-c) illustrate the original and reconstructed images by the proposed method and the Gaussian kernel-based re-gridding. The intensity profile was drawn over the gray line specified in Fig. 1(d). Figure 2 shows the original image of the digital brain phantom and the reconstructed images by the proposed method and Gaussian kernel-based re-gridding. The quantitative metrics such as SSIM and NRMSE were reported for both simulated phantoms in Table 1 comparing the conventional re-gridding technique and our proposed method. The impact of the parameter L(degree of spherical harmonics) on the quality of the reconstructed images is shown in Figures 4, and 5 for Shepp-Logan and brain simulated data with 7200 spokes, respectively. Blurring increases from peripheral area when we decrease the number of spherical harmonics.

Discussion and Conclusion

This study proposes a novel approach based on spherical harmonics that reconstruct directly in the spherical coordinates without any frequency interpolation and lead to higher SSIM and lower NRMSE values than the Gaussian kernel-based re-gridding method, according to Table 1. Also, as shown in Figure 1, the result of the proposed algorithm is in good agreement with the reference images concerning the intensity values, which could open new doors to quantitative imaging where the intensity values determine the accuracy and precision of the calculated maps. For sure, this algorithm needs more evaluation, and it is our plan for future studies.

Acknowledgements

No acknowledgement found.