Introduction

Two-dimensional (2D) Fast/Turbo Spin Echo (FSE/TSE) sequences are ubiquitous in clinical magnetic resonance imaging (MRI). Three-dimensional (3D) FSE can be acquired with isotropic resolution and reformatted into an arbitrary plane for visualizing complex anatomic structures, significantly reducing scan time compared to 2D FSE imaging.¹ To minimize excessive image blurring, commercial 3D FSE sequences typically utilize variable flip angles with long echo trains. However, long echo trains inevitably result in image blurring of tissues with relatively short T2. Approaches used to reduce image blurring without increasing scan time, such as reducing the minimum flip angle of the echo train, invariably result in a reduced signal-to-noise ratio (SNR). Increasing the number of excitations (NEX) is commonly used to improve SNR though this prolongs scan time.² To maintain both a reduced scan time and a high SNR, we investigated a deep learning-based method to yield 3D FSE images of high SNR in a reduced scan time compared to the standard high-SNR multi-NEX acquisitions.

Method

Figure 1 is an illustration of the proposed deep learning network. The inputs are two complex images from rapid 2-NEX acquisitions. The corresponding high-SNR images from 8-NEX acquisitions serve as the target. As noise maps could be calculated as the differences between two individual complex images, our proposed network can utilize inherent noise information in 2-NEX acquisitions to achieve image denoising.
Our network architecture consists of three modules:
1) In module 1, input 2NEX complex images are concatenated and transformed into 128-feature-map K by 6 convolution layers.
2) Module 2 contains two types of filters M and N, sharing the features K extracted from module 1. Filter-M has three processing steps. Firstly, a 2-kernel convolution is applied to K to generate M1. Secondly, the summation of M1 and the average of 2-NEX input is calculated as M2. Thirdly, a 64-kernel Conv-ReLU layer is used to generate feature map M3. Filter-N uses a Conv-BN-ReLU layer to generate feature map N1. Both filters M and N produce 64-feature maps M3 and N1.
3) In module 3, the first step is the concatenation of feature maps M3 and N1 to form feature map P, which is then reduced to 64-channels Q after applying another convolution layer. We apply the next 4 convolution layers with 64 kernels to save memory. The last layer is one convolution to transform the 64-channel S to 2-channel T. T and M2 are summed up to get the final output. The separation and concatenation operation in this model facilitates the capture, sharing, and passing of features.
Our network was trained in Pytorch framework using a combination of L2-loss and SSIM-loss³.
$$argmin_{f}\left \| f\left ( I_{2NEX}\right )-I_{8NEX} \right \|_{2}^{2}\times \left ( 1-ssim\left ( f\left ( I_{2NEX}\right )-I_{8NEX} \right ) \right )$$
For comparison, we applied the state-of-the-art denoising network DnCNN⁴ without modification to the same task. As a pure residual model, the DnCNN takes the average of 2-NEX images as input to match the output channels. A conventional denoising method BM3D⁵ was also undertaken for comparison.
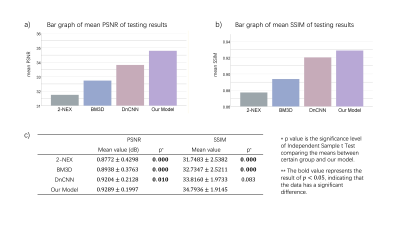
The datasets were collected using a 3D FSE/TSE VISTA^TM pulse sequence from a Philips Achieva TX 3.0T MRI (Philips Healthcare, Best, Netherlands). All MRI exams were conducted with approval of the institutional ethics review board. MR imaging parameters were as follows: TR/TE 900/33.6ms, 150 slices with isotropic resolution 0.8*0.8*0.8mm, ETL 42. Imaging acquisition time per NEX was 2.9 min. In total, 57 volunteer datasets with 8 NEX were collected. We used 50 datasets for training and 7 for testing. Independent sample t-tests were used to compare differences between PSNR and SSIM.

Results and Discussion

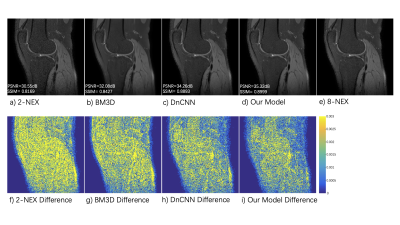
Figure 2 shows the testing results from a typical slice. Figure 2 a) - e) represent 2-NEX input, BM3D output, DnCNN output, our model output, and 8-NEX ground truth respectively. Plot f) - i) show the differences compared to 8-NEX ground truth. Both deep learning methods outperformed the traditional BM3D method not only in noise suppression level but also in preservation of structure detail. Simultaneous denoising and deblurring could be realized under the data-driven training strategy of neural networks. By utilizing the information from two individual NEX images, our model achieved better performance than DnCNN. Figure 3 illustrates the statistical analysis of testing results from different methods. Our proposed method outperformed both the traditional BM3D and state-of-the-art DnCNN in both PSNR and SSIM. This method has considerable clinical relevance in enabling the rapid acquisition of 3D FSE ME knee images with minimal loss of structural detail.

Conclusion

We propose a deep learning network to denoise 3D FSE/TSE MR images. Our proposed method helped reduce noise while preserving structure detail in knee MRI examinations.

Acknowledgements

This study was supported by a grant from the Innovation and Technology Commission of the Hong Kong SAR (Project MRP/001/18X), and a grant from the Research Grants Council of the Hong Kong SAR (Project SEG CUHK02).