4559
Dynamic MRI Reconstruction Combining Tensor Nuclear Norm and Casorati Matrix Nuclear Norm
Yinghao Zhang1, Yue Hu1, and Xin Lu2
1School of Electronics and Information Engineering, Harbin Institute of Technology, Harbin, China, 2School of Computer Science and Informatics, De Montfort University, Leicester, United Kingdom
1School of Electronics and Information Engineering, Harbin Institute of Technology, Harbin, China, 2School of Computer Science and Informatics, De Montfort University, Leicester, United Kingdom
Synopsis
Low-rank tensor models have been applied in accelerating dynamic magnetic resonance imaging (dMRI). Recently, a new tensor nuclear norm based on t-SVD has been proposed and applied to tensor completion. Inspired by the different properties of the tensor nuclear norm (TNN) and the Casorati matrix nuclear norm (MNN), we introduce a novel dMRI reconstruction method combining TNN and Casorati MNN, which we term as TMNN. Moreover, we convert the the TMNN dMRI reconstruction problem into a simple tensor completion problem, which can be efficiently solved by the alternating direction method of multipliers (ADMM).
Introduction
Dynamic magnetic resonance imaging (dMRI) is one of the most important non-invasive imaging modalities. However, it is usually challenging to obtain dynamic MR images with high spatiotemporal resolution within clinically acceptable scan time. Low-rank tensor priors1–3 have been successfully applied to reconstruct dynamic MR images from highly undersampled k-space data to accelerate dMRI. Recently, a new easy-computed tensor decomposition called tensor singular value decomposition4 (t-SVD) and a new tensor nuclear norm5 (TNN) have been proposed. Some works have adopted this framework to reconstruct dMRI. Banco et al.6 have applied t-SVD in dMRI reconstruction on a specific sampling mask. TNN and total variation (TV) regularizations7 are combined to improve the reconstruction of dMRI. Moreover, we notice that the TNN and Casorati matrix nuclear norm (MNN) has distinct properties, and thereby introduce a novel dMRI reconstruction method combining TNN and Casorati MNN, named TMNN.Methods
We denote the distortion-free dynamic MR tensor image as $$$\mathcal{X} \in \mathbb{C}^{n_{1} \times n_{2} \times n_{3}}$$$, where $$$n_1$$$, $$$n_2$$$ denote the spatial coordinates, and $$$n_3$$$ is the temporal coordinate. The data acquisition of dMRI can be modeled as$$ \mathbf b = A(\mathcal{X}) +\mathbf{n}$$
where $$$\mathbf b \in \mathbb{C}^{m}$$$ is the observed undersampled $$$k$$$-space data, $$$A: \mathbb{C}^{n_{1} \times n_{2} \times n_{3}} \rightarrow \mathbb{C}^m$$$ is the Fourier sampling operator, and $$$\mathbf{n} \in \mathbb{C}^{m}$$$ is the Gaussian distributed white noise. Inspired by the different properties of the TNN and the Casorati MNN, we propose a novel algorithm combining TNN and Casorati MNN, which we term as TMNN. The optimization problem can be formulated as follows
$$\min_{\mathcal{X}} \frac12 {\Vert A(\mathcal{X})-\mathbf b \Vert}_F^2+\lambda_1{\Vert \mathcal{X} \Vert}_*+\lambda_2{\Vert \mathbf C (\mathcal{X}) \Vert}_*$$
where $$${\Vert \mathcal{X} \Vert}_*$$$ is the tensor nuclear norm of $$${\cal X}$$$, $$$\mathbf C: \mathbb{C}^{n_{1} \times n_{2} \times n_{3}} \rightarrow \mathbb{C}^{n_{1} n_{2} \times n_{3}}$$$ unfolds the tensor into a Casorati matrix, $$${\Vert \mathbf C (\mathcal{X}) \Vert}_*$$$ denotes the nuclear norm of the Casorati matrix $$$\mathbf C(\mathcal{X})$$$, and $$$\lambda_1$$$, $$$\lambda_2$$$ are the regularization parameters.
We notice that the dMRI image $$$\mathcal{X}$$$ and its k-space $$$\hat{\mathcal{X}}$$$ have equal TNN and MNN. Thus, in the case of Cartesian sampling, where $$$ A=\mathcal{S}\mathcal{F}$$$, $$$\mathcal{S}$$$ is the under-sampling mask and $$$\mathcal{F}$$$ transforms the dMRI image into k-space, we can rewrite the reconstruction model above as a simple tensor completion optimization problem $$\min_{\hat{\mathcal{X}}} \frac12 {\Vert S \hat{\mathcal{X}}-\mathbf b \Vert}_F^2+\lambda_1{\Vert \hat{\mathcal{X}} \Vert}_*+\lambda_2{\Vert \mathbf C(\hat{\mathcal{X}}) \Vert}_*$$
which can be solved in alternating direction method of multipliers (ADMM).
Results and discussion
We evaluate the performance of the proposed TMNN method based on two data, i.e., a cardiac cine MR image with the size of $$$256\times 256\times 10$$$ and a myocardial perfusion MR image with the size of $$$190\times 90\times 70$$$. We assume that the measurements are acquired using the pseudo radial Cartesian sampling and variable density random sampling patterns under different undersampling ratios. We also add complex Gaussian white noise with the signal-to-noise ratio (SNR) of 20dB to the undersampled k-space data. The balancing parameters are experimentally set to be $$$\lambda_1=2.5e^{-3}$$$ and $$$\lambda_2=7.5e^{-3}$$$ for the noiseless case, and $$$\lambda_1=\lambda_2=0.1$$$ for the noisy case.In Fig.1, we compare the recovery results of the TMNN with MNN on a cine cardiac MR image from 30 radial lines (undersampling ratio $$$\sim$$$0.1) in the noiseless case. We observe that the proposed TMNN model outperforms the MNN method in providing more accurate reconstruction. Fig.2 shows the reconstruction of the cine cardiac MR image from the noisy undersampled measurements using 30 radial lines. In Fig.3, we plot the noisy reconstruction results of the perfusion MR image from the variable density random sampling trajectory with the undersampling ratio of 0.3. It is observed that the TMNN method generates less error compared with the MNN approach. The SNRs of the reconstructed dynamic image using TNN, MNN, and the proposed TMNN at different undersampling conditions are shown in Table.1. We observe that except for one case, the proposed TMNN consistently provides the best reconstruction results and improves the SNR by up to 2dB over the MNN method. In addition, it is shown that the improvement of the proposed TMNN over MNN is more significant in the noisy setting.
Conclusion
We proposed a novel combined regularization algorithm for dMRI reconstruction. By combining the tensor nuclear norm and the Casorati matrix nuclear norm, both the low-rank properties of the tensor and the Casorati matrix can be captured to exploit the spatiotemporal structures, and thus further improve the reconstruction performance. Moreover, we we convert the dynamic MRI reconstruction into a simple tensor completion problem, which can simplify the solution of the reconstruction problem. In order to efficiently solve the proposed optimization problem, we adopt the ADMM algorithm. Experimental results demonstrate the improved performance of the proposed TMNN model over the low-rank matrix recovery method.Acknowledgements
No acknowledgement found.References
- Kolda T G, Bader B W. Tensor decompositions and applications. SIAM review, 2009, 51(3): 455-500.
- He J, Liu Q, Christodoulou A G, et al. Accelerated high-dimensional MR imaging with sparse sampling using low-rank tensors. IEEE transactions on medical imaging, 2016, 35(9): 2119-2129.
- Cui K. Dynamic MRI reconstruction via weighted tensor nuclear norm regularizer. IEEE Journal of Biomedical and Health Informatics, 2021.
- Kilmer M E, Martin C D. Factorization strategies for third-order tensors. Linear Algebra and its Applications, 2011, 435(3): 641-658.
- Lu C, Feng J, Chen Y, et al. Tensor robust principal component analysis with a new tensor nuclear norm. IEEE transactions on pattern analysis and machine intelligence, 2019, 42(4): 925-938.
- Banco D, Aeron S, Hoge W S. Sampling and recovery of MRI data using low rank tensor models. 2016 38th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC). IEEE, 2016: 448-452.
- Ai J, Ma S, Du H, et al. Dynamic MRI reconstruction using tensor-SVD. 2018 14th IEEE International Conference on Signal Processing (ICSP). IEEE, 2018: 1114-1118.
Figures
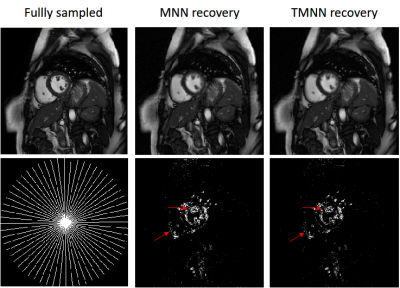
Fig.1: Recovery of the cine MRI data from the noiseless radial undersampled measurements using TMNN. The error images are shown in the second row.
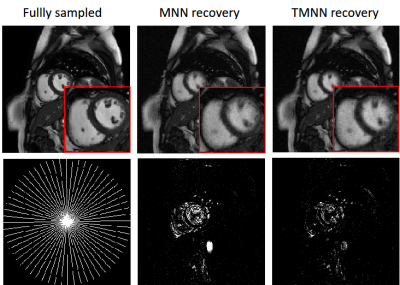
Fig.2: Recovery of the cine MRI data from the noisy radial undersampled measurements using MNN and TMNN. The error images are shown in the second row.
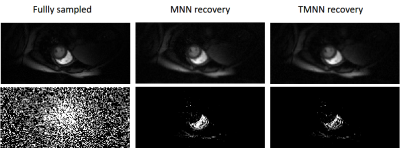
Fig.3: Recovery of the myocardial perfusion MRI data from the noisy variable density random undersampled measurements using MNN and TMNN. The error images are shown in the second row.

Table.1: SNR comparisons of TNN, MNN, and the proposed TMNN on two datasets using four sampling schemes.
DOI: https://doi.org/10.58530/2022/4559